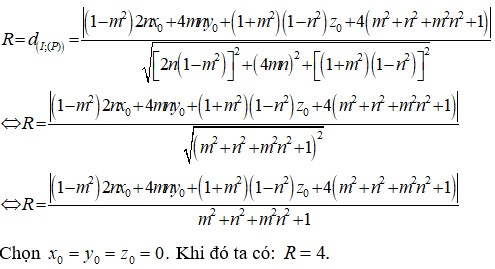Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình
1
-
m
2
2
n
.
x
+
4
m
n
.
y
+
1
+
m
2
1
-
n...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình 1 - m 2 2 n . x + 4 m n . y + 1 + m 2 1 - n 2 . z + 4 m 2 n 2 + m 2 + n 2 + 1 = 0 , với m, n là tham số thực tùy ý. Biết rằng mặt phẳng (P) luôn tiếp xúc với một mặt cầu cố định khi m, n thay đổi. Tìm bán kính mặt cầu đó?
A. 1
B. 2
C. 3
D. 4
Trong không gian với hệ tọa độ Oxyz, xét các điểm
A
0
;
0
;
1
,
B
m
;
0
;
0
,
C
0
;
n
;
0
,
D...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, xét các điểm A 0 ; 0 ; 1 , B m ; 0 ; 0 , C 0 ; n ; 0 , D 1 ; 1 ; 1 với m > 0, n > 0 và m + n = 1 . Biết rằng khi m, n thay đổi, tồn tại một mặt cầu cố định tiếp xúc với mặt phẳng (ABC) và đi qua D. Tính bán kính R của mặt cầu đó.
A. R = 1
B. R = 2 2
C. R = 3 2
D. R = 3 2
Trong không gian hệ trục tọa độ Oxyz, cho mặt phẳng
P
:
1
−
m
2
2
n
x
+
4
m
n
y
+
1
+
m
2
1
−
n
2...
Đọc tiếp
Trong không gian hệ trục tọa độ Oxyz, cho mặt phẳng P : 1 − m 2 2 n x + 4 m n y + 1 + m 2 1 − n 2 z + 4 m 2 + n 2 + m 2 n 2 + 1 = 0 . Biết (P) luôn tiếp xúc với mặt cầu cố định. Khi đó bán kính mặt cầu cố định đó là
A. 1
B. 2
C. 3
D. 4
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
(
P
)
:
x
+
y
–
z
–
4
0
và điểm M (1;–2;-2). Tọa độ điểm N đối xứng với điểm M qua mặt phẳng (P) là A. N (3;4;8) B. N (3;0;–4) C. N (3;0;8) D. N (3;4;–4)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( P ) : x + y – z – 4 = 0 và điểm M (1;–2;-2). Tọa độ điểm N đối xứng với điểm M qua mặt phẳng (P) là
A. N (3;4;8)
B. N (3;0;–4)
C. N (3;0;8)
D. N (3;4;–4)
Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng
d
:
x
-
2
2
y
-
1
z
4
và mặt cầu (S): (x-1)2+ (y-2)2 + (z-1)22. Hai mặt phẳng (P), (Q) chứa d và tiếp xúc với (S). Gọi M và N là tiếp điểm. Độ dài đoạn thẳng MN bằng
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d : x - 2 2 = y - 1 = z 4 và mặt cầu (S): (x-1)2+ (y-2)2 + (z-1)2=2. Hai mặt phẳng (P), (Q) chứa d và tiếp xúc với (S). Gọi M và N là tiếp điểm. Độ dài đoạn thẳng MN bằng
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x+2y-z+160 và mặt cầu (s): (x-2)2 + (y+1)2 + (z-3)29. Điểm M di động trên trên (S) và điểm N di động trên (P) sao cho độ dài đoạn thẳng MN ngắn nhất. Tọa độ điểm M là A. M(0;1;-1) B. M(0;-3;4) C. M(2;0;1) D. M(-2;2;-3)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x+2y-z+16=0 và mặt cầu (s): (x-2)2 + (y+1)2 + (z-3)2=9. Điểm M di động trên trên (S) và điểm N di động trên (P) sao cho độ dài đoạn thẳng MN ngắn nhất. Tọa độ điểm M là
A. M(0;1;-1)
B. M(0;-3;4)
C. M(2;0;1)
D. M(-2;2;-3)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):
(
x
-
1
)
2
+
(
y
-
2
)
2
+
(...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 2 ) 2 = 9 và mặt phẳng (P): 2x - 2y + z + 3 = 0. Gọi M(a;b;c) là điểm trên mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là lớn nhất. Khi đó:
A. a + b + c = 8.
B. a + b + c = 5.
C. a + b + c = 6.
D. a + b + c = 7.
Trong không gian Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
-
4
x
+
6
y
-
3
0
và điểm A(2;1;-2). Đườn...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 4 x + 6 y - 3 = 0 và điểm A(2;1;-2). Đường thẳng d đi qua A, tiếp xúc với (S) tại M luôn nằm trên mặt nón (N) cố định. Tọa độ tâm đường tròn đáy của (N) là H(a;b;c). Giá trị 3a-2b+c bằng
A. 8.
B. 4
C. 2.
D. 6 5
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
-
2
2
y
-
1
z
4
và mặt cầu (S):
(
x
-
1
)
2
+
(
y
-
2
)
2
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 2 2 = y - 1 = z 4 và mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 1 ) 2 = 2. Hai mặt phẳng (P) và (Q) chứa d và tiếp xúc với (S). Gọi M,N là tiếp điểm. Tính độ dài đoạn thẳng MN.
A. 2 2
B. 4 3
C. 6
D. 4