a: Xét tứ giác ABQM có 

AM//QB

AM=QB

DO đó: ABQM là hình bình hành

mà MA=MQ

nên ABQM là hình thoi

b: Xét tứ giác ANBQ có 

AN//BQ

AN=BQ

Do đó: ANBQ là hình bình hành

Suy ra: AQ//BN

c: Xét tứ giác ANPB có 

AN//BP

AN=BP

Do đó: ANPB là hình bình hành

mà NA=NP

nên ANPB là hình thoi

Xét ΔQPA có
AB là đường trung tuyến

AB=QP/2

Do đó:ΔQPA vuông tại A

hay \(\widehat{QAP}=90^0\)

a)

{BC=AD=2AB=2AE=2FDBC=2BE=2EC{BC=AD=2AB=2AE=2FDBC=2BE=2EC⇒AB=BE=EC=CD=FD=AF⇒AB=BE=EC=CD=FD=AF

tứ giác ECDF có: {FD//ECFD=EC{FD//ECFD=EC ⇒⇒ tứ giác ECDF là hình bình hành.

b)

tam giác DEC có: {DC=ECˆA=ˆC=60o{DC=ECA^=C^=60o⇒⇒tam giác DEC là tam giác đều.

⇒ˆDCE=ˆEDC=ˆDEC=60o⇒DCE^=EDC^=DEC^=60o

vì AD//BC nên ˆADC+ˆDCE=180o⇒ˆADC=1200ADC^+DCE^=180o⇒ADC^=1200

mà ˆADC=ˆADE+ˆEDCADC^=ADE^+EDC^

⇒ˆADE=60o⇒ADE^=60o

đồng thời ˆBAC=60oBAC^=60o

nên ˆADE=ˆBACADE^=BAC^

mặt khác: BE//AD

nên tứ giác ABED là hình thang cân.

c) c/m tương tự câu a, ta có: tứ giác ABEF là hình bình hành.

⇒⇒AB//FE ⇒ˆAEF=ˆEAB⇒AEF^=EAB^(1)

tam giác AFE có AF=FE nên tam giác AFE là tam giác cân

⇒ˆFAE=ˆFEA⇒FAE^=FEA^(2)

từ (1) và (2) ⇒ˆBAE=ˆEAF=ˆFEA=60o2=30o⇒BAE^=EAF^=FEA^=60o2=30o

tam giác FED có: {FD=DC=DEˆFDE=60o{FD=DC=DEFDE^=60o

do đó tam giác FED là tam giác đều.

⇒ˆFDE=ˆDEF=ˆEFD=180o3=60o⇒FDE^=DEF^=EFD^=180o3=60o

ta có: ˆAED=ˆAEF+ˆFED=30o+600=900

Giả sử ta có hình bình hành ABCD, đường chéo AC, AB=12cm, AC=10cm, `\hat(ABC)=150^o`.

`S_(ABC) = 1/2 . 10. 12 . sinABC = 30 (cm^2)`

Vì đường chéo AC chia hình bình hành ABCD ra 2 tam giác bằng nhau.

`=> S_(ABCD) = 2.S_(ABC) = 60(cm^2)`

`=>` B.

kẻ AH⊥BC; AB=10;BC=12

∠ABC=150

⇒∠ABH=30

xét ΔAHB có ∠H=90

⇒sin B=\(\dfrac{AH}{AB}\)⇒AH=\(\dfrac{1}{2}\).10=5

⇒S_ABCD=AH.AB=5.12=60

⇒chọn B

 !!!!!!!!!!!!!!!!!!!!!

\(\widehat{M}=360^0-80^0-55^0-60^0=165^0\)

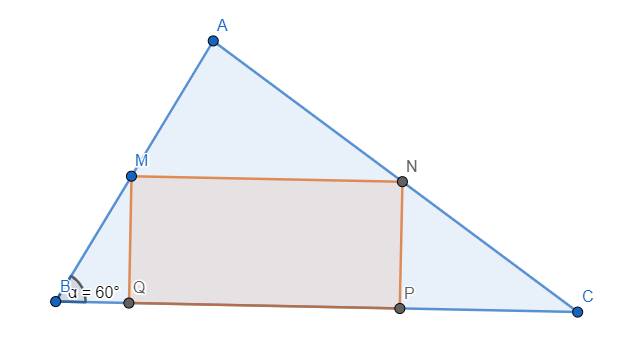
 Đặt \(MB=m>0\). \(\Rightarrow MQ=NP=\dfrac{m}{\sqrt{3}}\)

 Đặt \(AB=b>m\). Khi đó \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\) 

\(\Rightarrow MN=\dfrac{AM.BC}{AB}=\dfrac{\left(b-m\right).a}{b}=\left(1-\dfrac{m}{b}\right).a\) \(=a-\dfrac{a}{b}.m\)

\(\Rightarrow S_{MNPQ}=MN.NP=\dfrac{1}{\sqrt{3}}m\left(a-\dfrac{a}{b}.m\right)\)

\(=\dfrac{a}{b\sqrt{3}}\left(-m^2+bm\right)\)

 \(=\dfrac{a}{b\sqrt{3}}\left(-m^2+2m.\dfrac{b}{2}-\dfrac{b^2}{4}+\dfrac{b^2}{4}\right)\) 

\(=\dfrac{a}{b\sqrt{3}}\left[-\left(m-\dfrac{b}{2}\right)^2+\dfrac{b^2}{4}\right]\)

\(=-\dfrac{a}{\sqrt{3}}\left(m-\dfrac{b}{2}\right)^2+\dfrac{ab}{4\sqrt{3}}\) \(\le\dfrac{ab}{4\sqrt{3}}\), suy ra \(S_{MNPQ}\le\dfrac{ab}{4\sqrt{3}}\)

 Dấu "=" xảy ra \(\Leftrightarrow m=\dfrac{b}{2}\) hay M là trung điểm của đoạn AB.

 Vậy để diện tích hình chữ nhật MNPQ lớn nhất khi và chỉ khi M là trung điểm AB.