PH
Những câu hỏi liên quan
Cho tg ABC, trên cạnh AB lấy D sao cho AD= 12, DB= 6. Trên cạnh AC lấy E sao cho AE= 16, EC= 8. Cạnh BC- 30. CMR: DE//BC
Bài làm
Ta có: \(\frac{AD}{AB}=\frac{12}{6+12}=\frac{12}{18}=\frac{2}{3}\)
\(\frac{AE}{AC}=\frac{16}{8+16}=\frac{16}{24}=\frac{2}{3}\)
=> \(\frac{AD}{AB}=\frac{AE}{AC}\left(=\frac{2}{3}\right)\)
Xét tam giác ADE và tam giác ABC có:
\(\frac{AD}{AB}=\frac{AE}{AC}\)( cmt )
Góc A chung.
=> Tam giác ADE ~ Tam giác ABC ( c.g.c )
=> \(\frac{DE}{BC}=\frac{AD}{AB}=\frac{AE}{AC}\)
Xét tam giác ABC có:
\(\frac{DE}{BC}=\frac{AD}{AB}=\frac{AE}{AC}\)
Theo định lí Thales đảo.
=> DE // BC ( đpcm )
# Học tốt #
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB<AC. Lấy D thuộc AC; E thuộc AB: góc ADE=góc B. Gọi K;H thứ tự là hình chiếu của E;D trên BC.
a) CMR: AD.AE.BC2=AB+AC+DE2
b) CMR: BE.BA+CD.CA.+HK.BC=BC2
c) Cho biết AB=6 cm; AC=8 cm. Tính DE+EK+DH
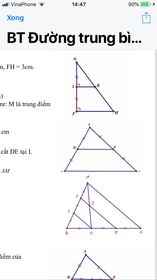
Bài 3: Cho hình vẽ bên. Biết DE = 4 cm, D là trung điểm AB, E là trung điểm AC a) Tính BC. b) Gọi M là trung điểm BC. AM cắt DE tại I. Cmr: I là trung điểm DE. c) AM cắt BE tại G. Cmr: IG=1/6 AM
Hình thứ 2 nha
cho tam giác ABC, A = 130, trên cạnh BC lấy E sao cho CE = CA. Vữ tia phân giác ACB cắt AB tại D, CMR : a) DE = DA, b) Tính BED nhớ vẽ hình nha
a: Xét ΔADC và ΔEDC có
CA=CE
\(\widehat{ACD}=\widehat{ECD}\)
CD chung
Do đó: ΔADC=ΔEDC
Suy ra: DA=DE
Đúng 0
Bình luận (1)
Cho tam giác ABC cân tại A có góc A = 20 độ. Trên AB lấy D sao cho AD = BC. Vẽ DE // BC (E thuộc BC) và DE = AB
a,CMR : tam giác EDA = tam giác ABC
b, góc DAE = ?
c, CMR: Tam giác ACE đều
Cho t/g ABC vuông tại A có AB=4cm, Ac=3cm. Trên AB lấy D sao cho AD=AC (D nằm giữa A và B), trên tia đối của Ca lấy E sao cho AE=Ab (C nằm giữa A và E). Kẻ AH ⊥⊥Bc. Đoạn thẳng AH cắt DE tại M (M nằm giữa D và E)
a/ Tính BC
b/ CMR t/g ABC = t/g AED
c/ CMR t/g AMD cân tại M
*Nhớ vẽ hình nha!*
Bài toán 3 : Tìm UCLN. a) ƯCLN ( 10 ; 28) e) ƯCLN (24 ; 84 ; 180) b) ƯCLN (24 ; 36) g) ƯCLN (56 ; 140) c) ƯCLN (16 ; 80 ; 176) h) ƯCLC (12 ; 14 ; 8 ; 20) d) ƯCLN (6 ; 8 ; 18) k) ƯCLN ( 7 ; 9 ; 12 ; 21)Bài toán 4 : Tìm ƯC. a) ƯC(16 ; 24) e) ƯC(18 ; 77) b) ƯC(60 ; 90) g) ƯC(18 ; 90) c) ƯC(24 ; 84) h) ƯC(18 ; 30 ; 42) d) ƯC(16 ; 60) k) ƯC(26 ; 39 ; 48)Bài toán 5 : Tìm BCNN của. a) BCNN( 8 ; 10 ; 20) f) BCNN(56 ; 70 ; 126) b) BCNN(16 ; 24) g) BCNN(28 ; 20 ; 30) c) BCNN(60 ; 140) h) BCNN(34 ; 32 ; 20...
Đọc tiếp
Bài toán 3 : Tìm UCLN. a) ƯCLN ( 10 ; 28) e) ƯCLN (24 ; 84 ; 180) b) ƯCLN (24 ; 36) g) ƯCLN (56 ; 140) c) ƯCLN (16 ; 80 ; 176) h) ƯCLC (12 ; 14 ; 8 ; 20) d) ƯCLN (6 ; 8 ; 18) k) ƯCLN ( 7 ; 9 ; 12 ; 21)
Bài toán 4 : Tìm ƯC. a) ƯC(16 ; 24) e) ƯC(18 ; 77) b) ƯC(60 ; 90) g) ƯC(18 ; 90) c) ƯC(24 ; 84) h) ƯC(18 ; 30 ; 42) d) ƯC(16 ; 60) k) ƯC(26 ; 39 ; 48)
Bài toán 5 : Tìm BCNN của. a) BCNN( 8 ; 10 ; 20) f) BCNN(56 ; 70 ; 126) b) BCNN(16 ; 24) g) BCNN(28 ; 20 ; 30) c) BCNN(60 ; 140) h) BCNN(34 ; 32 ; 20) d) BCNN(8 ; 9 ; 11) k) BCNN(42 ; 70 ; 52) e) BCNN(24 ; 40 ; 162) l) BCNN( 9 ; 10 ; 11)
Bài toán 6 : Tìm bội chung (BC) của. a) BC(13 ; 15) e) BC(30 ; 105) b) BC(10 ; 12 ; 15) g) BC( 84 ; 108) c) BC(7 ; 9 ; 11) h) BC(98 ; 72 ; 42) d) BC(24 ; 40 ; 28) k) BC(68 ; 208 ; 100)
Please
GIúp Mình với
bạn nên chia nhỏ đề bài ra
cái này dễ mak bn ơi,bn đăng
từng bài một mn sẽ giải chứ
bn đăng như này chưa chắc
đã cs ng giải cho bn
nhìn cái này chắc loạn thị luôn ak
Xem thêm câu trả lời
cho hình vuông ABCD có cạnh bằng a.Gọi E là một điểm bất kì trên cạnh BC . Qua B vẽ đường thẳng vuông góc với tia DE tại H, đường thẳng này cắt tia DC tại F
a) CMR : 5 điểm A,B,H,C,D nằm trên một đường tròn
b) CMR : DE.HE=BE.CE
c) Tính độ dài đoạn thẳng DH theo a khi E là trung điểm của BC
cho góc xOy bằng 30 và điểm A nằm trong góc xOy. B và D theo thứ tự là hình chiếu của điểm A trên Ox và Oy. Trên tia đói của tia BA lấy điểm C sao cho BC= BA, trên tia đối của tia AD lấy điểm E sao cho DE=DA. cmr tam giác OCE đều
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M là điểm bất kỳ trên cạnh BC(M khác B,C),D và E lần lượt là các hình chiếu vuông góc của M trên AB và AC.
a)CMR:AM=DE và tìm vị trí của điểm M trên BC để tứ giác ADME là hình vuông .
b)CMR : góc DHE =90
c):vẽ DK vuông góc BC tại K, EN vuông góc BC tại N. CMR:MK=HN
d):CMR :S DKNE=S DME +S DHE


