Cho tam giác ABC vuông tại A, đường cao AH Biết AB=7,2cm, AC 9,6cm. Tính HB và HC
ND
Những câu hỏi liên quan
Cho tam giac ABC vuông tại A ,biết AC=12cm;AB=9cm;AH=7,2cm;HC=5,4cm;HB=9,6cm. Đường cao AH. Cho tia phân giác của góc BAC cắt BC tại D
Tính BD và CD
Cho tam giác ABC vuông tại A có đường cao AH . Trong các đoạn thẳng sau đây : AB,AC,BC,AH,HB,HC hãy tính các đoạn thẳng còn lại nếu biết :
a. AB=6cm , AC=8cm
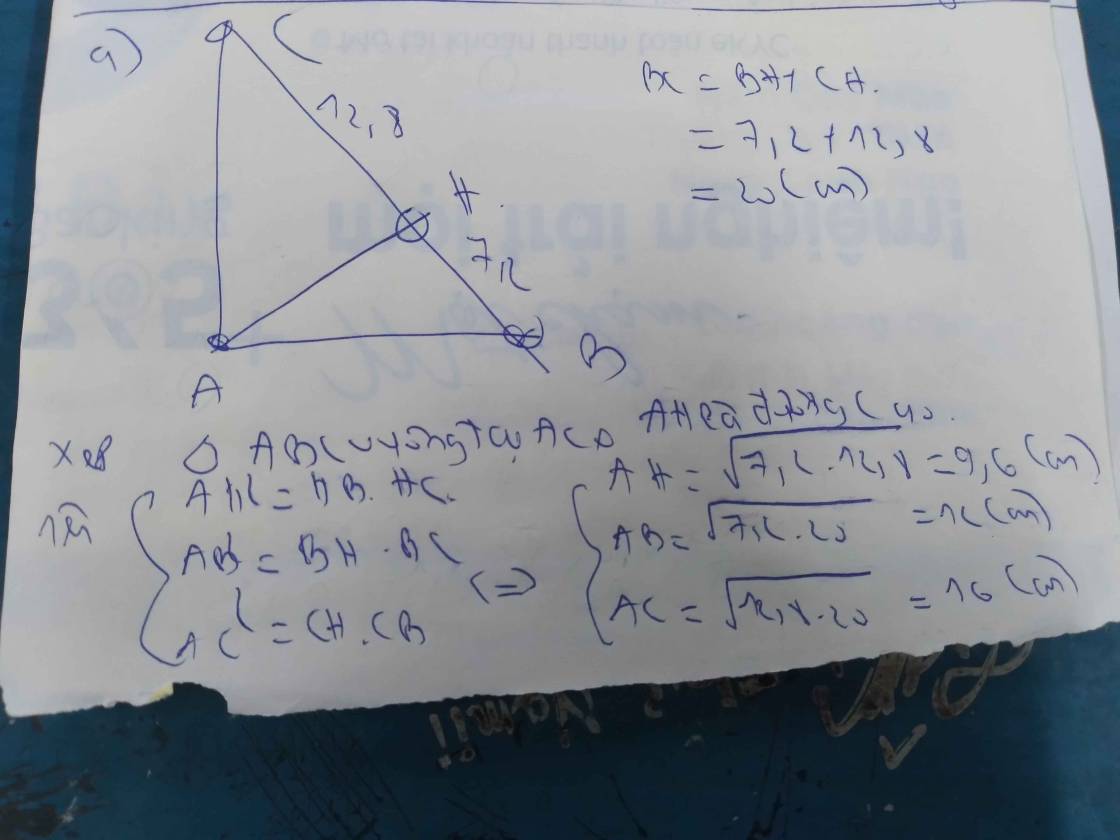
b. AH=9,6cm ,HC=12,8cm
c. AH=12cm , BC=25cm
d. AB=15cm , HB=9cm
e. HB=12,5cm , HC=7,2cm
a.
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm) theo định lý Pitago
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=3,6$ (cm) theo định lý Pitago
$CH=BC-BH=10-3,6=6,4$ (cm)
b.
Áp dụng HTL trong tam giác vuông:
$AH^2=BH.CH$
$\Rightarrow BH=\frac{AH^2}{CH}=\frac{AH^2}{CH}=\frac{9,6^2}{12,8}=7,2$ (cm)
$BC=BH+CH=7,2+12,8=20$ (cm)
$AB=\sqrt{AH^2+BH^2}=\sqrt{9,6^2+7,2^2}=12$ (cm) theo Pitago
$AC=\sqrt{BC^2-AB^2}=\sqrt{20^2-12^2}=16$ (cm) theo Pitago
Đúng 1
Bình luận (0)
c.
$AB.AC=AH.BC=12.25=300$
$AB^2+AC^2=BC^2=625$
$(AB+AC)^2-2AB.AC=625$
$AB+AC=\sqrt{625+2AB.AC}=\sqrt{625+2.300}=35$
Áp dụng Viet đảo thì $AB,AC$ là nghiệm của:
$X^2-35X+300=0$
$\Rightarrow (AB,AC)=(20,15)$ (giả sử $AB>AC$)
$BH=\sqrt{AB^2-AH^2}=\sqrt{20^2-12^2}=16$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm)
Đúng 1
Bình luận (0)
d.
Áp dụng HTL trong tam giác vuông:
$AB^2=BH.BC$
$\Rightarrow BC=\frac{AB^2}{HB}=\frac{15^2}{9}=25$ (cm)
$CH=BC-BH=25-9=16$ (cm)
Áp dụng HTL:
$AH=\sqrt{BH.CH}=\sqrt{9.16}=12$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)
e.
$BC=BH+CH=12,5+7,2=19,7$ (cm)
$AH=\sqrt{HB.HC}=\sqrt{12,5.7,2}=3\sqrt{10}$ (cm)
$AB=sqrt{AH^2+BH^2}=\sqrt{(3\sqrt{10})^2+12,5^2}=\frac{\sqrt{985}}{2}$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{(3\sqrt{10})^2+7,2^2}=\frac{3\sqrt{394}}{5}$ (cm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, đg cao AH. Tính các đoạn còn lại nếu biết
a.HB=7,2cm; HC=12,8cm
b.AC=16cm; HB=7,2cm
c.AH=9,6cm; HB/HC=18/32
Cho tam giác ABC vuông tại A, đường cao AH, AC=16cm, HB=7,2cm. Tính AH, AB, BC, HC
AC^2=HC*CB
=>HC(HC+7,2)=16^2=256
=>HC^2+7,2*HC-256=0
=>HC=12,8cm
AH=căn 12,8*7,2=9,6cm
BC=12,8+7,2=20cm
AB=căn 7,2*20=12(cm)
AC=căn 12,8*20=16(cm)
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A ,AB=9 cm ;AC=12 cm ;BC=15cm ; AH=7,2cm ; HC=5,4cm ; HB =9,6 cm . Đường cao AH .Cho tia phân giác của góc BAC cắt BC tại A .Tính BD và CD
Giúp mình với ak!!!!
1. Cho tam giác ABC vuông tại A, biết AB/AC=5/7 và đường cao AH=15cm. Tính HB, HC.
2. Cho tam giác ABC vuông tại A, có đường cao AH=14cm và HB/HC=1/4. Tính chu vi tam giác ABC.
1: AB/AC=5/7
=>HB/HC=(AB/AC)^2=25/49
=>HB/25=HC/49=k
=>HB=25k; HC=49k
ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>1225k^2=15^2=225
=>k^2=9/49
=>k=3/7
=>HB=75/7cm; HC=21(cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH.TRong cá đoạn thẳng sau AB,AC,BC,AH,HB,HC hãy tính độ dài các đoạn thẳng còn lại nếu:
a, AB=6cm;AC=9cm
b,AB=15cm;HB=9cm
c,AC=44cm;Bc=55cm
d,AC=40cm;AH=24cm
e,AH=9,6cm;HC=12,8cm
f,CH=72cm;BH=12,5cm
g,AH=12cm;trung tuyến AM=13cm
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+9^2=117\)
hay \(BC=3\sqrt{13}\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AB\cdot AC=AH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{12\sqrt{13}}{13}\left(cm\right)\\CH=\dfrac{27\sqrt{13}}{13}\left(cm\right)\\AH=\dfrac{18\sqrt{13}}{13}\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hình vẽ bên, biết tam giác abc vuông tại a, ah vuông góc với bc (h thuộc bc). AB = 9cm, AH = 7,2cm, HC = 9,6cm A.Tính cạnh ac B.Chứng minh tích các cạnh: AH.BC = AB.AC
Xem chi tiết
a:
ΔAHC vuông tại H
=>\(AC^2=AH^2+HC^2\)
=>\(AC^2=144\)
=>AC=12(cm)
b: \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot AB\cdot AC\)
=>\(AH\cdot BC=AB\cdot AC\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A ( AB < AC ), cho đường cao AH :
a/ cm : tam giác HBA đồng dạng ABC
b/ cm : AH = HB. HC
c/ vẽ phân giác góc B cắt AC tại E . từ C kẻ đường thẳng vuông góc với BE tại F . cm : EF. BC = EC . FC
d/ vẽ trung tuyến của tam giác ABC . tính diện tích tứ giác AICF biết rằng HB =5,4cm và HC = 9,6cm
* chỉ giúp câu d thôi nhé... *