Giúp em 2 mấy bài này với ạ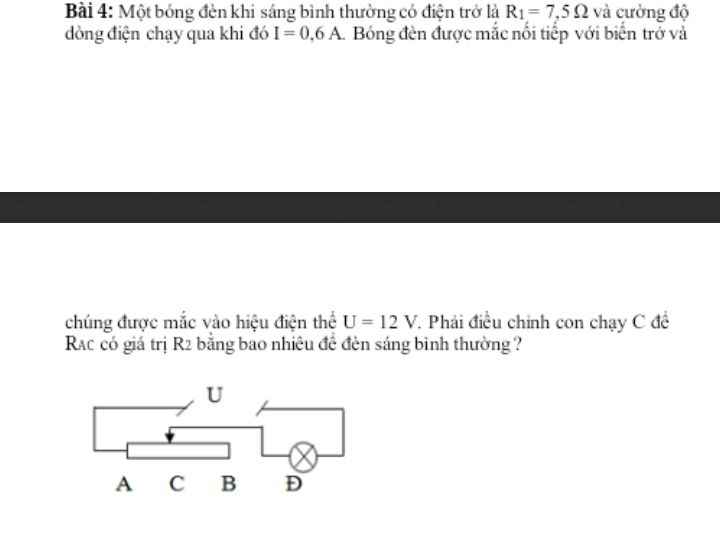
HD
Những câu hỏi liên quan
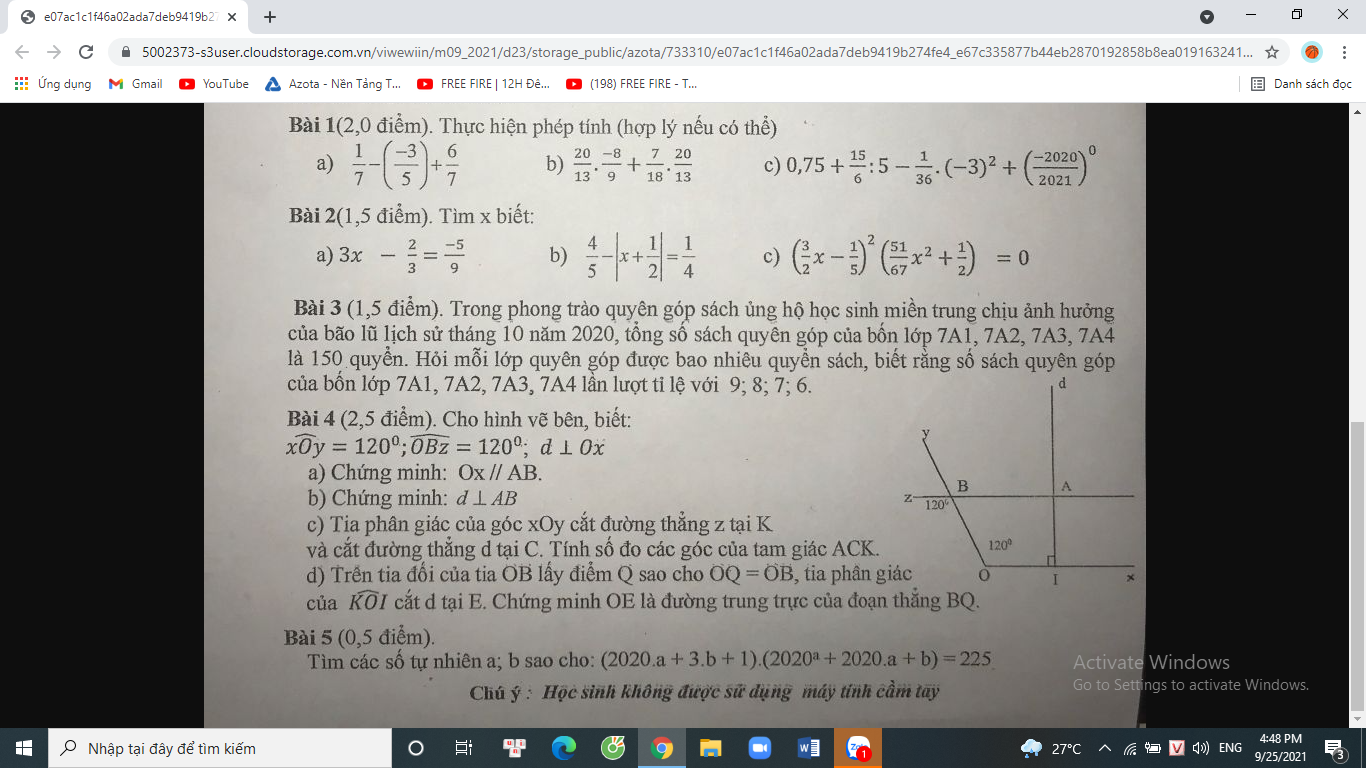
Giúp em mấy bài này với ạ . Em cần gấp lắm ạ
mng giúp em bài mấy bài này với ạ
Bài 1:
a: Xét tứ giác NPIK có
\(\widehat{NKP}=\widehat{NIP}\left(=90^0\right)\)
Do đó: NPIK là tứ giác nội tiếp
hay N,P,I,K cùng thuộc 1 đường tròn
b: Xét tứ giác MKHI có
\(\widehat{MKH}+\widehat{MIH}=180^0\)
Do đó: MKHI là tứ giác nội tiếp
hay M,K,H,I cùng thuộc 1 đường tròn
Đúng 0
Bình luận (0)
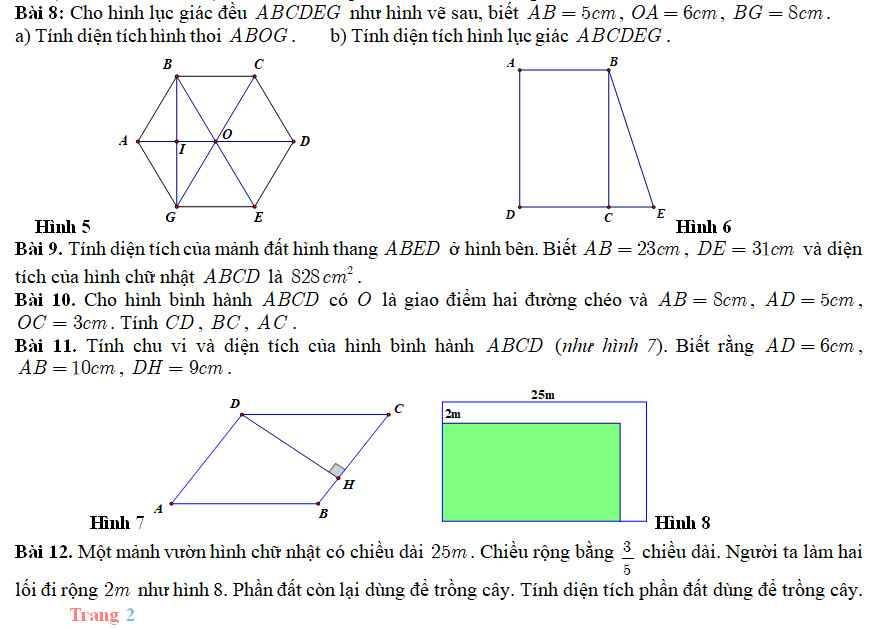 chỉ giúp em mấy bài này với ạ em đng cần gấp ạ
chỉ giúp em mấy bài này với ạ em đng cần gấp ạ
Bài 12:
Chiều rộng mảnh vườn:
25 x 3/5 = 15(m)
Diện tich phần trồng cây có chiều dài:
25 - 2=23(m)
Diện tích phần trồng cây có chiều rộng:
15 - 2 = 13(m)
Diện tích phần trồng cây:
23 x 13= 299(m2)
Đ.số: 299m2
Đúng 1
Bình luận (0)
12: Chiều rộng là 25*3/5=15m
Chiều dài mảnh đất trồng cây là 25-2=23m
Chiều rộng mảnh đất trồng cây là 15-2=13m
Diện tích mảnh đất trồng cây là:
23*13=299m2
Đúng 1
Bình luận (0)
Bài 9:
Độ dài cạnh BC:
828 : 23=36(m)
Độ dài CE:
31- 23= 8(m)
Diện tích mảnh đất tam giác BCE:
(36 x 8):2= 144(m2)
Diện tích mảnh đất hình thang ABED:
828 + 144= 972(m2)
Đ.số: 972m2
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
giúp em bài này với ạ, em chưa học mấy số như này:''0,04'' đâu ạ!![]()

a: Chiều rộng là 80*3/4=60m=6000cm
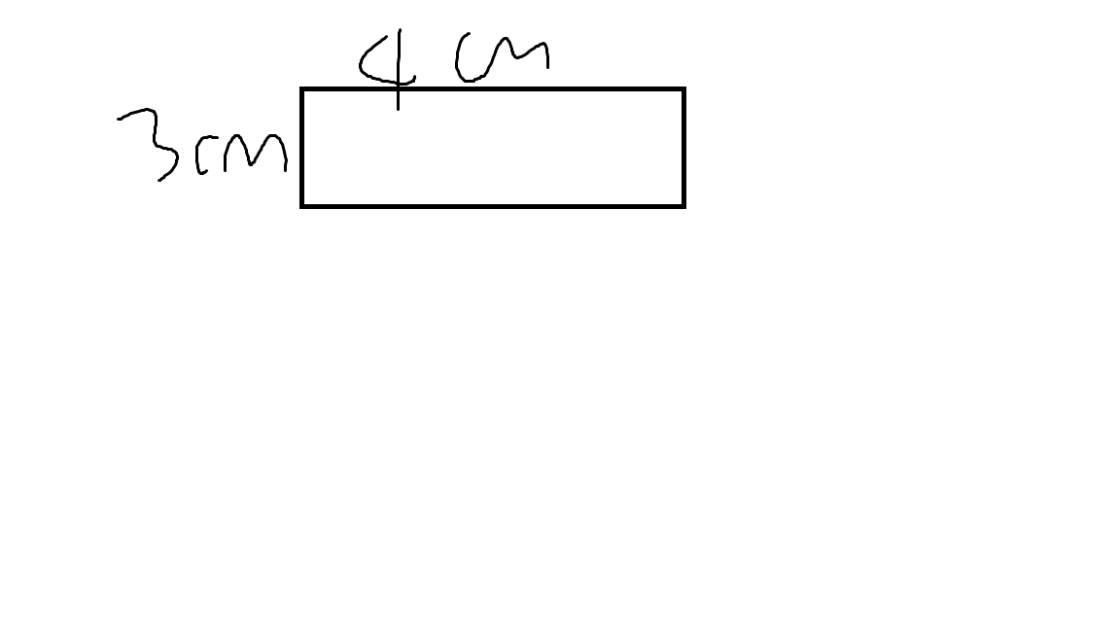
b: Chiều dài trên bản đồ là:
8000/2000=4cm
Chiều rộng trên bản đồ là:
6000/2000=3cm
Đúng 0
Bình luận (0)
giải giúp em mấy bài này với ạ
Giải mấy bài này giúp em với ạ
giúp em mấy bài này với ạ huhu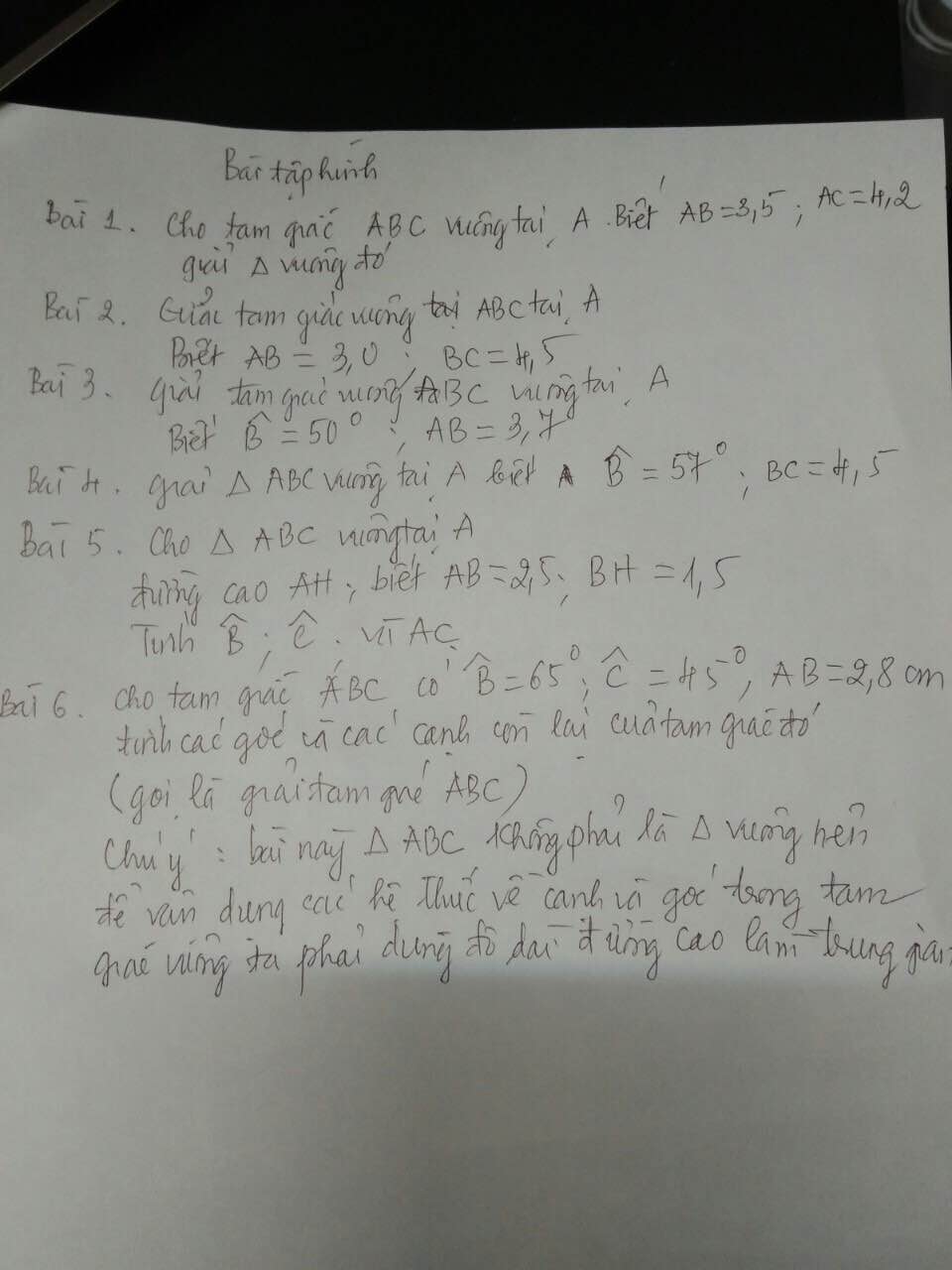
mọi người giúp em mấy bài này với ạ =(((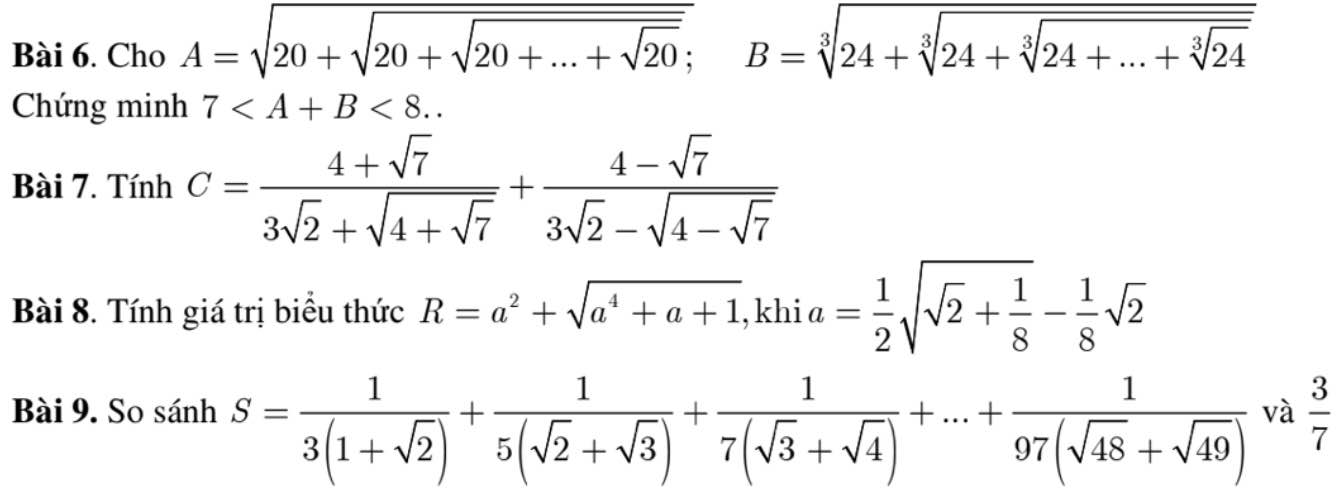
Bài 7:
Ta có: \(C=\dfrac{4+\sqrt{7}}{3\sqrt{2}+\sqrt{4+\sqrt{7}}}+\dfrac{4-\sqrt{7}}{3\sqrt{2}-\sqrt{4-\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}\left(4+\sqrt{7}\right)}{6+\sqrt{8+2\sqrt{7}}}+\dfrac{\sqrt{2}\left(4-\sqrt{7}\right)}{6-\sqrt{8-2\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}\left(4+\sqrt{7}\right)}{7+\sqrt{7}}+\dfrac{\sqrt{2}\left(4-\sqrt{7}\right)}{7-\sqrt{7}}\)
\(=\dfrac{\sqrt{2}\left(\sqrt{7}-1\right)\left(4+\sqrt{7}\right)}{6\sqrt{7}}+\dfrac{\sqrt{2}\left(\sqrt{7}+1\right)\left(4-\sqrt{7}\right)}{6\sqrt{7}}\)
\(=\dfrac{\sqrt{2}\left(-3+3\sqrt{7}+3+3\sqrt{7}\right)}{6\sqrt{7}}\)
\(=\sqrt{2}\)
Đúng 2
Bình luận (0)
6.
Ta có:
\(A=\sqrt{20+\sqrt{20+...+\sqrt{20}}}>\sqrt{20+\sqrt{\dfrac{1}{16}}}=\dfrac{9}{2}\)
\(B=\sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{24}}}>\sqrt[3]{24}=\sqrt[3]{\dfrac{192}{8}}>\sqrt[3]{\dfrac{125}{8}}=\dfrac{5}{2}\)
\(\Rightarrow A+B>\dfrac{9}{2}+\dfrac{5}{2}=7\)
\(A=\sqrt[]{20+\sqrt[]{20+...+\sqrt[]{20}}}< \sqrt[]{20+\sqrt[]{20+...+\sqrt[]{25}}}=5\)
\(B=\sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{24}}}< \sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{27}}}=3\)
\(\Rightarrow A+B< 5+3=8\)
Đúng 1
Bình luận (0)
8.
Ta có:
\(a=\dfrac{1}{2}\sqrt{\sqrt{2}+\dfrac{1}{8}}-\dfrac{\sqrt{2}}{8}\Rightarrow\dfrac{1}{2}\sqrt{\sqrt{2}+\dfrac{1}{8}}=a+\dfrac{\sqrt{2}}{8}\)
\(a^2=\dfrac{1}{4}\left(\sqrt{2}+\dfrac{1}{8}\right)+\dfrac{1}{32}-\dfrac{\sqrt{2}}{4}.\dfrac{1}{2}\sqrt{\sqrt{2}+\dfrac{1}{8}}\)
\(=\dfrac{\sqrt{2}}{4}+\dfrac{1}{32}+\dfrac{1}{32}-\dfrac{\sqrt{2}}{4}\left(a+\dfrac{\sqrt{2}}{8}\right)\)
\(=\dfrac{\sqrt{2}}{4}+\dfrac{1}{16}-\dfrac{\sqrt{2}}{4}a-\dfrac{1}{16}\)
\(=\dfrac{\sqrt{2}}{4}\left(1-a\right)\)
\(\Rightarrow a^4=\dfrac{1}{8}\left(a^2-2a+1\right)\)
\(\Rightarrow a^4+a+1=\dfrac{1}{8}\left(a^2-2a+1\right)+a+1=\dfrac{1}{8}\left(a+3\right)^2\)
\(\Rightarrow R=a^2+\dfrac{\sqrt{2}}{4}\left(a+3\right)=\dfrac{\sqrt{2}}{4}\left(1-a\right)+\dfrac{\sqrt{2}}{4}\left(a+3\right)=\sqrt{2}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp em giải mấy bài tập này với ạ em cảm ơn






