(x+1).(2x-3)-3.(x-2)=2.(x-1)^2
Giải phương trình trên
CL
Những câu hỏi liên quan
Bài 1:giải các phương trình sau:
a) x-5=1/3(x+2) b)x/3+x/4=x/5-x/6 c)3x(2x-3)-3(3+2x^2)=0 d)(x1)^2-x(x+1)+3(x-2)+5=0
Bài 2:giải các phương trình sau
a)x/2-2x/3+1/4=2/3 b)x-2 trên 3 -2x-3 trên 4= x-1 c)5x-2 trên 3+1/2=2(x-1)-3(x-1) trên 6
\(x-5=\frac{1}{3\left(x+2\right)}\left(đkxđ:x\ne-2\right)\)
\(< =>3\left(x-5\right)\left(x+2\right)=1\)
\(< =>3\left(x^2-3x-10\right)=1\)
\(< =>x^2-3x-10=\frac{1}{3}\)
\(< =>x^2-3x-\frac{31}{3}=0\)
giải pt bậc 2 dễ r
\(\frac{x}{3}+\frac{x}{4}=\frac{x}{5}-\frac{x}{6}\)
\(< =>\frac{4x+3x}{12}=\frac{6x-5x}{30}\)
\(< =>\frac{7x}{12}=\frac{x}{30}< =>12x=210x\)
\(< =>x\left(210-12\right)=0< =>x=0\)
\(3x\left(2x-3\right)-3\left(3+2x^2\right)=0\)
\(< =>6x^2-9x-9-6x^2=0\)
\(< =>-9x-9=0< =>9x+9=0\)
\(< =>x=-\frac{9}{9}=-1\)
Xem thêm câu trả lời
Bài 1.*) Giải phương trình a) 1 + 5x 2x + 7 b) 3 – 5(x+3) x + 1 c) **) Giải bất phương trình và biểu diễn tập nghiệm trên trục số a) 4x + 5 2x – 2 b) 2 (x - 2) 5x + 2 (mũi tên kia thêm gạch ngang câub) giúp mình nha :))
Đọc tiếp
Bài 1.*) Giải phương trình
a) 1 + 5x = 2x + 7 b) 3 – 5(x+3) = x + 1 c)
**) Giải bất phương trình và biểu diễn tập nghiệm trên trục số
a) 4x + 5 > 2x – 2 b) 2 (x - 2) < 5x + 2 (mũi tên kia thêm gạch ngang câub) giúp mình nha :))
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:a)
(
x
+
1
)
2
+
2
x
2
(
2
x
+
3
)
2
−
(
x
−...
Đọc tiếp
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) ( x + 1 ) 2 + 2 x 2 < ( 2 x + 3 ) 2 − ( x − 3 ) 2 ;
b) 2 x ( x − 7 ) + ( 3 − x ) 2 > 3 ( x + 1 ) 2
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:a)
(
2
x
+
3
)
(
2
x
−
1
)
(
2
x
−
5
)
2
b)
(
x
−
1
)
(
x
+
2
)
(...
Đọc tiếp
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) ( 2 x + 3 ) ( 2 x − 1 ) < ( 2 x − 5 ) 2
b) ( x − 1 ) ( x + 2 ) < ( x − 1 ) 2 + 3
aGiải phương trình |x-1|+|x-2|=|2x-3|
b)Giải phương trình 1/(x−2 )+ 2/(x−3) − 3/(x−5) = 1/(x^2 −5x+6)
Giải các bất phương trình sau rồi biểu diễn tập nghiệm của chúng trên trục số:1) left(x+3right)^2-3left(2x-1right)xleft(x-4right)2) 1+dfrac{x+1}{3}dfrac{2x-1}{6}-23) x-dfrac{2x-7}{4} dfrac{2x}{3}-dfrac{2x+3}{2}-14) dfrac{2x+1}{x-3}le25) dfrac{12-3x}{2x+6}36) x^2+3x-4le07) dfrac{5}{5x-1} dfrac{-3}{5-3x}8) left(2x-1right)left(3-2xright)left(1-xright)0
Đọc tiếp
Giải các bất phương trình sau rồi biểu diễn tập nghiệm của chúng trên trục số:
1) \(\left(x+3\right)^2-3\left(2x-1\right)>x\left(x-4\right)\)
2) \(1+\dfrac{x+1}{3}>\dfrac{2x-1}{6}-2\)
3) \(x-\dfrac{2x-7}{4}< \dfrac{2x}{3}-\dfrac{2x+3}{2}-1\)
4) \(\dfrac{2x+1}{x-3}\le2\)
5) \(\dfrac{12-3x}{2x+6}>3\)
6) \(x^2+3x-4\le0\)
7) \(\dfrac{5}{5x-1}< \dfrac{-3}{5-3x}\)
8) \(\left(2x-1\right)\left(3-2x\right)\left(1-x\right)>0\)
1: \(\Leftrightarrow x^2+6x+9-6x+3>x^2-4x\)
=>-4x<12
hay x>-3
2: \(\Leftrightarrow6+2x+2>2x-1-12\)
=>8>-13(đúng)
4: \(\dfrac{2x+1}{x-3}\le2\)
\(\Leftrightarrow\dfrac{2x+1-2x+6}{x-3}< =0\)
=>x-3<0
hay x<3
6: =>(x+4)(x-1)<=0
=>-4<=x<=1
Đúng 1
Bình luận (0)
Giải bất phương trình và biểu diễn tập nghiệm trên trục số
(x-2)(2x-3)+3(x+4)<2(x+1)2-4x
=>2x^2-3x-4x+6+3x+8<2x^2+4x+2-4x
=>2x^2-4x+14<2x^2+2
=>-4x<-12
=>x>3
Đúng 0
Bình luận (0)
Bài 2: giải phương trình sau a) X^4-x^2-20b) (x+1)^4-x^2+2)^20c)3x^2-2x-80Bài 3: giải phương trình sau a) x^3-0,250b) x^4+2x^3+x^20c) x^3-10d) 6x^2-7x+20Mong có người giải giùm xin kẻm ơn :
Đọc tiếp
Bài 2: giải phương trình sau
a) \(X^4\)-\(x^2\)-2=0
b) (x+1)\(^4\)-x\(^2\)+2)\(^2\)=0
c)3x\(^2\)-2x-8=0
Bài 3: giải phương trình sau
a) x\(^3\)-0,25=0
b) x\(^4\)+2x\(^3\)+x\(^2\)=0
c) x\(^3\)-1=0
d) 6x\(^2\)-7x+2=0
Mong có người giải giùm xin kẻm ơn :>
Bài 3:
b: \(\Leftrightarrow x^2\left(x+1\right)^2=0\)
hay \(x\in\left\{0;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)=0\)
=>x-1=0
hay x=1
d: \(\Leftrightarrow6x^2-3x-4x+2=0\)
\(\Leftrightarrow\left(2x-1\right)\left(3x-2\right)=0\)
hay \(x\in\left\{\dfrac{1}{2};\dfrac{2}{3}\right\}\)
Đúng 3
Bình luận (0)
\(\left(2x-5\right)\left(\sqrt{x+3}-1\right)=2x^2-x-10\)
giải phương trình trên
Ta có:\(\left(2x-5\right)\left(\sqrt{x+3}-1\right)=2x^2-x-10\)
\(\Leftrightarrow\left(2x-5\right)\left(\sqrt{x+3}-1\right)-\left(2x^2-x-10\right)=0\)
\(\Leftrightarrow\left(2x-5\right).\dfrac{\left(x+2\right)}{\sqrt{x+3}+1}-\left(2x-5\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left(2x-5\right)\left(x+2\right)\left(\dfrac{1}{\sqrt{x+3}+1}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+2=0\\\dfrac{1}{\sqrt{x+3}+1}-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-2\\\dfrac{1}{\sqrt{x+3}+1}=1\left(1\right)\end{matrix}\right.\)
Giải (1) ta có:
\(\left(1\right)\Leftrightarrow1=\sqrt{x+3}+1\)
\(\Leftrightarrow\sqrt{x+3}=0\)
\(\Leftrightarrow x+3=0\)
\(\Leftrightarrow x=-3\)
Vậy,phương trình có 3 nghiệm là.....
Đúng 1
Bình luận (0)
Giải phương trình và bất phương trình sau:
a
)
|
3
x
|
x
+
6
b
)
x
+
2
x
-
2
-
1
x
2
x...
Đọc tiếp
Giải phương trình và bất phương trình sau:
a ) | 3 x | = x + 6 b ) x + 2 x - 2 - 1 x = 2 x x - 2 c ) ( x + 1 ) ( 2 x – 2 ) – 3 > – 5 x – ( 2 x + 1 ) ( 3 – x )
a) |3x| = x + 6 (1)
Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0
Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:
+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0
Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)
Do đó x = 3 là nghiệm của phương trình (1).
+ ) Phương trình -3x = x + 6 với điều kiện x < 0
Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)
Do đó x = -3/2 là nghiệm của phương trình (1).
Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}
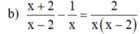
ĐKXĐ: x ≠ 0, x ≠ 2
Quy đồng mẫu hai vễ của phương trình, ta được:
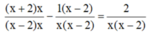
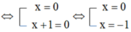
Vậy tập nghiệm của phương trình là S = {-1}
c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)
⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)
⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x
⇔ 10x ≥ 2 ⇔ x ≥ 1/5
Tập nghiệm: S = {x | x ≥ 1/5}
Đúng 0
Bình luận (0)