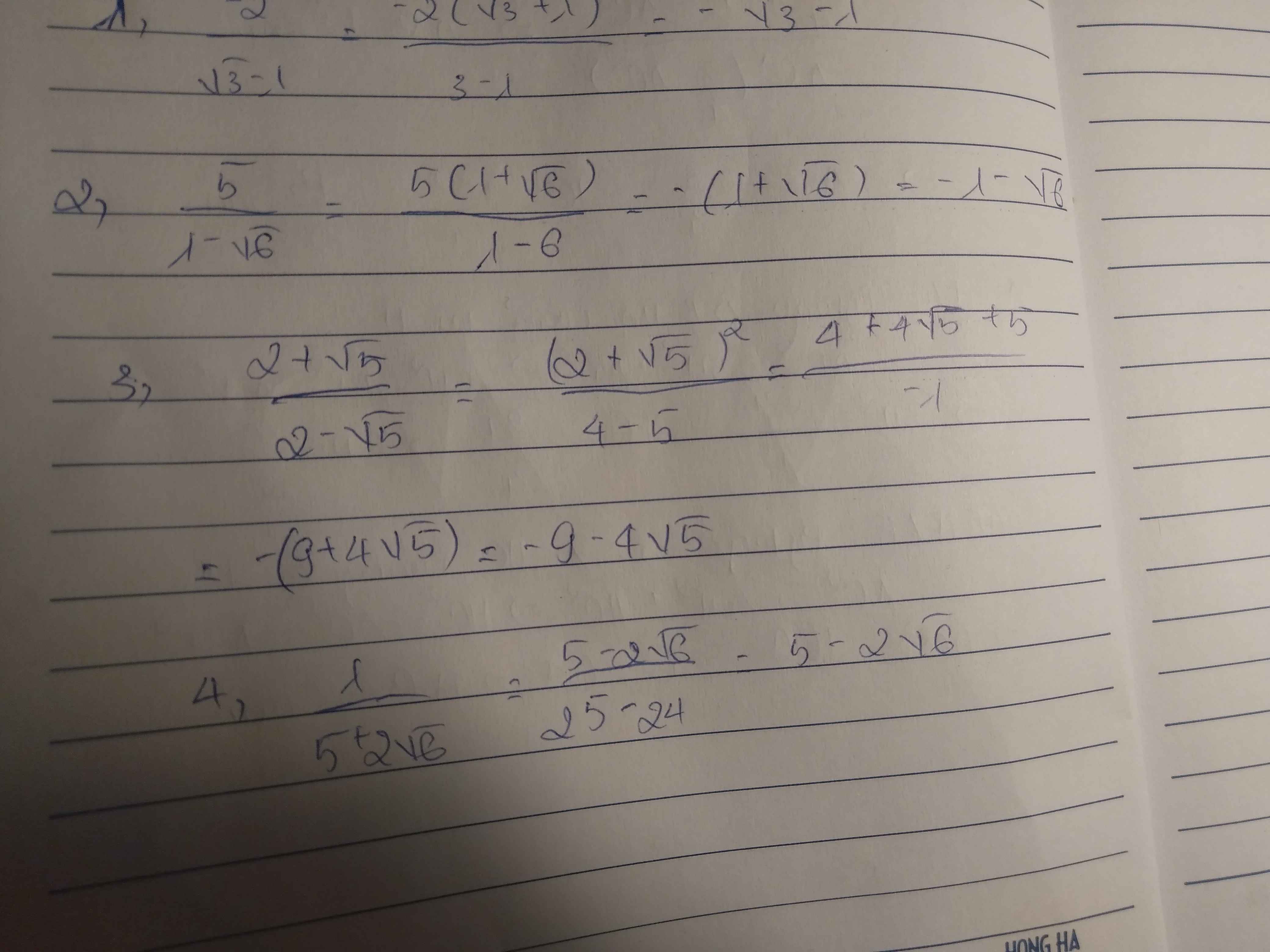\(\dfrac{\sqrt{6-2\sqrt{5}}}{2-\sqrt{20}}\)
H24
Những câu hỏi liên quan
dfrac{2sqrt{3}-3sqrt{2}}{sqrt{6}}-dfrac{2}{1-sqrt{3}}dfrac{4}{sqrt{6}+sqrt{2}}-dfrac{sqrt{54}+sqrt{2}}{sqrt{3}+1}dfrac{5+2sqrt{5}}{sqrt{5}}-dfrac{20}{5+sqrt{5}}-sqrt{20}Bài 2sqrt{25x^2-10x+1}sqrt{4x^2+8x+4}sqrt{x^2-3}+1xsqrt{7-2x}sqrt{x^2+7}sqrt{9x-27}+dfrac{1}{2}sqrt{4x-12}-9sqrt{dfrac{x-3}{9}}2
Đọc tiếp
\(\dfrac{2\sqrt{3}-3\sqrt{2}}{\sqrt{6}}-\dfrac{2}{1-\sqrt{3}}\)
\(\dfrac{4}{\sqrt{6}+\sqrt{2}}-\dfrac{\sqrt{54}+\sqrt{2}}{\sqrt{3}+1}\)
\(\dfrac{5+2\sqrt{5}}{\sqrt{5}}-\dfrac{20}{5+\sqrt{5}}-\sqrt{20}\)
Bài 2
\(\sqrt{25x^2-10x+1}=\sqrt{4x^2+8x+4}\)
\(\sqrt{x^2-3}+1=x\)
\(\sqrt{7-2x}=\sqrt{x^2+7}\)
\(\sqrt{9x-27}+\dfrac{1}{2}\sqrt{4x-12}-9\sqrt{\dfrac{x-3}{9}}=2\)
\(2,\\ a,PT\Leftrightarrow\sqrt{\left(5x-1\right)^2}=\sqrt{4\left(x+1\right)^2}\\ \Leftrightarrow\left|5x-1\right|=2\left|x+1\right|\\ \Leftrightarrow\left[{}\begin{matrix}5x-1=2\left(x+1\right)\\1-5x=2\left(x+1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=3\\7x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{7}\end{matrix}\right.\)
\(b,ĐK:x^2-3\ge0\\ PT\Leftrightarrow\sqrt{x^2-3}=x-1\\ \Leftrightarrow x^2-3=x^2-2x+1\\ \Leftrightarrow2x=4\Leftrightarrow x=2\left(tm\right)\\ c,ĐK:x\le\dfrac{7}{2}\\ PT\Leftrightarrow7-2x=x^2+7\\ \Leftrightarrow x^2+2x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=2\left(tm\right)\end{matrix}\right.\\ d,ĐK:x\ge3\\ PT\Leftrightarrow3\sqrt{x-3}+\dfrac{1}{2}\cdot2\sqrt{x-3}-9\cdot\dfrac{1}{3}\sqrt{x-3}=2\\ \Leftrightarrow\sqrt{x-3}=2\\ \Leftrightarrow x-3=4\Leftrightarrow x=7\left(tm\right)\)
Đúng 2
Bình luận (1)
Bài 1:
d: Ta có: \(\dfrac{5+2\sqrt{5}}{\sqrt{5}}-\dfrac{20}{5+\sqrt{5}}-\sqrt{20}\)
\(=\sqrt{5}+2-5+\sqrt{5}-2\sqrt{5}\)
=-3
Đúng 1
Bình luận (1)
1. dfrac{-2}{sqrt{3}-1}2. dfrac{5}{1-sqrt{6}}3. dfrac{2+sqrt{5}}{2-sqrt{5}}4. dfrac{1}{5+2sqrt{6}}5. dfrac{sqrt{5}+2}{sqrt{5}-2}6. dfrac{5sqrt{2}-2sqrt{5}}{sqrt{2}-sqrt{5}}7. dfrac{sqrt{20}-3sqrt{10}}{3-sqrt{2}}8. dfrac{6-2sqrt{5}}{3+sqrt{5}}9. dfrac{9+4sqrt{5}}{sqrt{5}+2}
Đọc tiếp
1. \(\dfrac{-2}{\sqrt{3}-1}\)
2. \(\dfrac{5}{1-\sqrt{6}}\)
3. \(\dfrac{2+\sqrt{5}}{2-\sqrt{5}}\)
4. \(\dfrac{1}{5+2\sqrt{6}}\)
5. \(\dfrac{\sqrt{5}+2}{\sqrt{5}-2}\)
6. \(\dfrac{5\sqrt{2}-2\sqrt{5}}{\sqrt{2}-\sqrt{5}}\)
7. \(\dfrac{\sqrt{20}-3\sqrt{10}}{3-\sqrt{2}}\)
8. \(\dfrac{6-2\sqrt{5}}{3+\sqrt{5}}\)
9. \(\dfrac{9+4\sqrt{5}}{\sqrt{5}+2}\)
5 câu:1) dfrac{sqrt{3}+sqrt{2}}{sqrt{6}+2}-dfrac{sqrt{3}-sqrt{2}}{sqrt{6}-2}2) dfrac{3}{sqrt{5}-sqrt{2}}-dfrac{2}{2-sqrt{2}}+dfrac{1}{sqrt{3}+sqrt{2}}3) dfrac{12}{sqrt{5}+1}-dfrac{4}{sqrt{5}+2}+dfrac{20}{3+sqrt{5}}4) dfrac{5}{3-sqrt{7}}-dfrac{2}{sqrt{2}+sqrt{3}}-dfrac{1}{sqrt{2}-1}5) dfrac{sqrt{12}-6}{sqrt{8}-sqrt{24}}-dfrac{3+sqrt{3}}{sqrt{3}}-dfrac{4}{sqrt{7}-1}
Đọc tiếp
5 câu:
1) \(\dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{6}+2}-\dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{6}-2}\)
2) \(\dfrac{3}{\sqrt{5}-\sqrt{2}}-\dfrac{2}{2-\sqrt{2}}+\dfrac{1}{\sqrt{3}+\sqrt{2}}\)
3) \(\dfrac{12}{\sqrt{5}+1}-\dfrac{4}{\sqrt{5}+2}+\dfrac{20}{3+\sqrt{5}}\)
4) \(\dfrac{5}{3-\sqrt{7}}-\dfrac{2}{\sqrt{2}+\sqrt{3}}-\dfrac{1}{\sqrt{2}-1}\)
5) \(\dfrac{\sqrt{12}-6}{\sqrt{8}-\sqrt{24}}-\dfrac{3+\sqrt{3}}{\sqrt{3}}-\dfrac{4}{\sqrt{7}-1}\)
* Tính
a. A=\(\left(\dfrac{6+\sqrt{20}}{3+\sqrt{5}}+\dfrac{\sqrt{14}-\sqrt{2}}{\sqrt{7}-1}\right):\left(2+\sqrt{2}\right)\)
b. B=\(\sqrt{5-2\sqrt{6}}+\sqrt{5+2\sqrt{6}}-\dfrac{11}{2\sqrt{3}+1}\)
a: Ta có: \(A=\left(\dfrac{6+\sqrt{20}}{3+\sqrt{5}}+\dfrac{\sqrt{14}-\sqrt{2}}{\sqrt{7}-1}\right):\left(2+\sqrt{2}\right)\)
\(=\left(2+\sqrt{2}\right):\left(2+\sqrt{2}\right)\)
=1
b: Ta có: \(B=\sqrt{5-2\sqrt{6}}+\sqrt{5+2\sqrt{6}}-\dfrac{11}{2\sqrt{3}+1}\)
\(=\sqrt{3}-\sqrt{2}+\sqrt{3}+\sqrt{2}-2\sqrt{3}+1\)
=1
Đúng 1
Bình luận (0)
Tính:
\(A=3\sqrt{20}-\sqrt{45}+2\sqrt{18}+\sqrt{72}\)
\(B=\dfrac{12}{3-\sqrt{5}}-\dfrac{16}{\sqrt{5}+1}\)
\(C=10\sqrt{\dfrac{1}{5}}+\dfrac{1}{5}\sqrt{125}-2\sqrt{20}\)
\(E=\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(F=\sqrt{6+2\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
a) Ta có: \(A=3\sqrt{20}-\sqrt{45}+2\sqrt{18}+\sqrt{72}\)
\(=6\sqrt{5}-3\sqrt{5}+6\sqrt{2}+6\sqrt{2}\)
\(=3\sqrt{5}+12\sqrt{2}\)
b) Ta có: \(B=\dfrac{12}{3-\sqrt{5}}-\dfrac{16}{\sqrt{5}+1}\)
\(=\dfrac{12\left(3+\sqrt{5}\right)}{4}-\dfrac{16\left(\sqrt{5}-1\right)}{4}\)
\(=3\left(3+\sqrt{5}\right)-4\left(\sqrt{5}-1\right)\)
\(=9+3\sqrt{5}-4\sqrt{5}+4\)
\(=13-\sqrt{5}\)
c) Ta có: \(C=10\sqrt{\dfrac{1}{5}}+\dfrac{1}{5}\sqrt{125}-2\sqrt{20}\)
\(=\dfrac{10}{\sqrt{5}}+\dfrac{1}{5}\cdot5\sqrt{5}-2\cdot2\sqrt{5}\)
\(=2\sqrt{5}+\sqrt{5}-4\sqrt{5}\)
\(=-\sqrt{5}\)
Đúng 2
Bình luận (0)
e) Ta có: \(E=\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\sqrt{3}+1-2+\sqrt{3}\)
\(=2\sqrt{3}-1\)
f) Ta có: \(F=\sqrt{6+2\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{5}+1-\sqrt{5}+2\)
=3
Đúng 1
Bình luận (0)
Tính:
\(A=3\sqrt{20}-\sqrt{45}+2\sqrt{18}+\sqrt{72}\)
\(B=\dfrac{12}{3-\sqrt{5}}-\dfrac{16}{\sqrt{5}+1}\)
\(C=10\sqrt{\dfrac{1}{5}}+\dfrac{1}{5}\sqrt{125}-2\sqrt{20}\)
\(E=\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(F=\sqrt{6+2\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
e) Ta có: \(E=\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\sqrt{3}+1-2+\sqrt{3}\)
\(=2\sqrt{3}-1\)
f) Ta có: \(F=\sqrt{6+2\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{5}+1-\sqrt{5}+2\)
=3
Đúng 3
Bình luận (0)
a) Ta có: \(A=3\sqrt{20}-\sqrt{45}+2\sqrt{18}+\sqrt{72}\)
\(=6\sqrt{5}-3\sqrt{5}+6\sqrt{2}+6\sqrt{2}\)
\(=3\sqrt{5}+12\sqrt{2}\)
b) Ta có: \(B=\dfrac{12}{3-\sqrt{5}}-\dfrac{16}{\sqrt{5}+1}\)
\(=\dfrac{12\left(3+\sqrt{5}\right)}{4}-\dfrac{16\left(\sqrt{5}-1\right)}{4}\)
\(=3\left(3+\sqrt{5}\right)-4\left(\sqrt{5}-1\right)\)
\(=9+3\sqrt{5}-4\sqrt{5}+4\)
\(=13-\sqrt{5}\)
Đúng 1
Bình luận (0)
Giải 5 câu sau:
1. \(\dfrac{\sqrt{5}+2}{\sqrt{5}-2}\)
2. \(\dfrac{5\sqrt{2}-2\sqrt{5}}{\sqrt{2}-\sqrt{5}}\)
3. \(\dfrac{\sqrt{20}-3\sqrt{10}}{3-\sqrt{5}}\)
4. \(\dfrac{6-2\sqrt{5}}{3+\sqrt{5}}\)
5. \(\dfrac{9+4\sqrt{5}}{\sqrt{5}+2}\)
1) \(\dfrac{\sqrt{5}+2}{\sqrt{5}-2}=9+4\sqrt{5}\)
2) \(\dfrac{5\sqrt{2}-2\sqrt{5}}{\sqrt{2}-\sqrt{5}}=\dfrac{\sqrt{10}\left(\sqrt{5}-\sqrt{2}\right)}{-\left(\sqrt{5}-\sqrt{2}\right)}=-\sqrt{10}\)
3) \(\dfrac{\sqrt{20}-3\sqrt{10}}{3-\sqrt{5}}=\dfrac{\sqrt{10}\left(\sqrt{5}-3\right)}{-\left(\sqrt{5}-3\right)}=-\sqrt{10}\)
4) \(\dfrac{6-2\sqrt{5}}{3+\sqrt{5}}=\dfrac{\left(6-2\sqrt{5}\right)\left(3-\sqrt{5}\right)}{4}=\dfrac{18-6\sqrt{5}-6\sqrt{5}+10}{4}=\dfrac{28-12\sqrt{5}}{4}=7-3\sqrt{5}\)
5)\(\dfrac{9+4\sqrt{5}}{\sqrt{5}+2}=\sqrt{5}+2\)
Đúng 2
Bình luận (0)
\(A=\dfrac{1}{\sqrt{8}+\sqrt{7}}+\sqrt{175}+2\sqrt{2}\\ B=\left(5+2\sqrt{6}\right)\cdot\left(49-20\sqrt{6}\right)\cdot\sqrt{5-2\sqrt{6}}\)
\(C=\dfrac{1}{2}\left(\sqrt{6}+\sqrt{5}\right)^2-\dfrac{1}{4}\sqrt{120}-\sqrt{\dfrac{15}{2}}\)
\(D=\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}+\dfrac{1}{4}\sqrt{8}\right)\cdot3\sqrt{6}\)
\(A=\sqrt{8}-\sqrt{7}+5\sqrt{7}+2\sqrt{2}\\ =2\sqrt{2}-\sqrt{7}+5\sqrt{7}+2\sqrt{2}\\ =4\sqrt{2}+4\sqrt{7}\)
Đúng 0
Bình luận (0)
\(B=\left(3+2\sqrt{6}+2\right)\left(25-20\sqrt{6}+24\right)\sqrt{3-2\sqrt{6}+2}\\ =\left(\sqrt{3}+\sqrt{2}\right)^2\left(5-2\sqrt{6}\right)^2\left(\sqrt{3}-\sqrt{2}\right)\\ =\left(\sqrt{3}+\sqrt{2}\right)\left(3-2\sqrt{6}+2\right)^2\\ =\left(\sqrt{3}-\sqrt{2}\right)^3\\ =9\sqrt{3}-11\sqrt{2}\)
Đúng 0
Bình luận (0)
\(C=\dfrac{1}{2}\left(11+2\sqrt{30}\right)-\dfrac{\sqrt{30}}{2}-\dfrac{\sqrt{30}}{2}\\
=\dfrac{11}{2}+\sqrt{30}-\sqrt{30}\\
=\dfrac{11}{2}\)
Đúng 0
Bình luận (0)
Tính
\(\dfrac{\left(5+2\sqrt{6}\right)\left(49-20\sqrt{6}\right)\sqrt{5-2\sqrt{6}}}{9\sqrt{3}-11\sqrt{2}}\)
\(\dfrac{\dfrac{\sqrt{2+\sqrt{3}}}{2}}{\dfrac{\sqrt{2+\sqrt{3}}}{2}-\dfrac{2}{\sqrt{6}}+\dfrac{\sqrt{2+\sqrt{3}}}{2\sqrt{3}}}\)
\(\dfrac{1+\dfrac{\sqrt{3}}{2}}{1+\sqrt{1+\dfrac{\sqrt{3}}{2}}}+\dfrac{1-\dfrac{\sqrt{3}}{2}}{1-\sqrt{1-\dfrac{\sqrt{3}}{2}}}\)
a) \(\dfrac{\left(5+2\sqrt{6}\right)\left(49-20\sqrt{6}\right)\sqrt{5-2\sqrt{6}}}{9\sqrt{3}-11\sqrt{2}}\)
\(=\dfrac{\left(245-100\sqrt{6}+98\sqrt{6}-240\right)\sqrt{\left(\sqrt{2}-\sqrt{3}\right)^2}}{9\sqrt{3}-11\sqrt{2}}\)
\(=\dfrac{\left(5-2\sqrt{6}\right)\left(\sqrt{3}-\sqrt{2}\right)}{9\sqrt{3}-11\sqrt{2}}\)
\(=\dfrac{5\sqrt{3}-5\sqrt{2}-2\sqrt{18}+2\sqrt{12}}{9\sqrt{3}-11\sqrt{2}}\)
\(=\dfrac{5\sqrt{3}-5\sqrt{2}-6\sqrt{2}+4\sqrt{3}}{9\sqrt{3}-11\sqrt{2}}\)
\(=\dfrac{9\sqrt{3}-11\sqrt{2}}{9\sqrt{3}-11\sqrt{2}}\)
\(=1\)
Đúng 0
Bình luận (0)
b)
\(\dfrac{\dfrac{\sqrt{2+\sqrt{3}}}{2}}{\dfrac{\sqrt{2+\sqrt{3}}}{2}-\dfrac{2}{\sqrt{6}}+\dfrac{\sqrt{2+\sqrt{3}}}{2\sqrt{3}}}\)
\(=\dfrac{\dfrac{\sqrt{2+\sqrt{3}}}{2}}{\dfrac{\sqrt{2+\sqrt{3}}}{2}-\dfrac{2\sqrt{6}}{6}+\dfrac{\sqrt{2+\sqrt{3}}}{2\sqrt{3}}}\)
\(=\dfrac{\dfrac{\sqrt{2+\sqrt{3}}}{2}}{\dfrac{\sqrt{2+\sqrt{3}}}{2}-\dfrac{\sqrt{6}}{3}+\dfrac{\sqrt{2+\sqrt{3}}}{2\sqrt{3}}}\)
\(=\dfrac{\dfrac{\sqrt{2+\sqrt{3}}}{2}}{\dfrac{3\sqrt{3\left(2+\sqrt{3}\right)}-2\sqrt{18}+3\sqrt{2+\sqrt{3}}}{6\sqrt{3}}}\)
\(=\dfrac{\dfrac{\sqrt{2+\sqrt{3}}}{2}}{\dfrac{3\sqrt{6+3\sqrt{3}-6\sqrt{2}+3\sqrt{2+\sqrt{3}}}}{6\sqrt{3}}}\)
\(=\dfrac{3\sqrt{\left(2+\sqrt{3}\right)\cdot3}}{3\sqrt{6+3\sqrt{3}}-6\sqrt{2}+3\sqrt{2+\sqrt{3}}}\)
\(=\dfrac{3\sqrt{\left(2+\sqrt{3}\right)\cdot3}}{3\left(\sqrt{6+3\sqrt{3}}-2\sqrt{2}+\sqrt{2+\sqrt{3}}\right)}\)
\(=\dfrac{\sqrt{\left(2+\sqrt{3}\right)\cdot3}}{\sqrt{6+3\sqrt{3}}-2\sqrt{2}+\sqrt{2+\sqrt{3}}}\)
\(=\dfrac{\sqrt{6+3\sqrt{3}}}{\sqrt{6+3\sqrt{3}}-2\sqrt{2}+\sqrt{2+\sqrt{3}}}\)
\(=\dfrac{\sqrt{\left(6+3\sqrt{3}\right)\left(-\sqrt{3}+2+\sqrt{3}\right)}}{-2\sqrt{3}}\)
\(=\dfrac{\sqrt{\left(6+3\sqrt{3}\right)\cdot2}}{-2\sqrt{3}}\)
\(=\dfrac{\sqrt{12+6\sqrt{3}}}{-2\sqrt{3}}\)
\(=\dfrac{\sqrt{\left(3+\sqrt{3}\right)^2}}{-2\sqrt{3}}\)
\(=\dfrac{3+\sqrt{3}}{-2\sqrt{3}}\)
\(=-\dfrac{\left(3+\sqrt{3}\right)\sqrt{3}}{6}\)
\(=-\dfrac{3\sqrt{3}+3}{6}\)
\(=-\dfrac{3\left(\sqrt{3}+3\right)}{6}\)
\(=-\dfrac{\sqrt{3}+1}{2}\)
Đúng 0
Bình luận (2)
\(\dfrac{1+\dfrac{\sqrt{3}}{2}}{1+\sqrt{1+\dfrac{\sqrt{3}}{2}}}+\dfrac{1-\dfrac{\sqrt{3}}{2}}{1-\sqrt{1-\dfrac{\sqrt{3}}{2}}}\)
\(=\dfrac{\left(1+\dfrac{\sqrt{3}}{2}\right)\cdot\left(1-\sqrt{1+\dfrac{\sqrt{3}}{2}}\right)}{-\dfrac{\sqrt{3}}{2}}+\dfrac{\left(1-\dfrac{\sqrt{3}}{2}\right)\cdot\left(1+\sqrt{1-\dfrac{\sqrt{3}}{2}}\right)}{\dfrac{\sqrt{3}}{2}}\)
\(=\dfrac{1-\sqrt{1+\dfrac{\sqrt{3}}{2}}+\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{3\left(1+\dfrac{\sqrt{3}}{2}\right)}}{2}}{-\dfrac{\sqrt{3}}{2}}+\dfrac{\left(1-\dfrac{\sqrt{3}}{2}\right)\cdot\left(1+\sqrt{1-\dfrac{\sqrt{3}}{2}}\right)\cdot2}{\sqrt{3}}\)
\(=\dfrac{1-\sqrt{1+\dfrac{\sqrt{3}}{2}}+\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{3+\dfrac{3\sqrt{3}}{2}}}{2}}{-\dfrac{\sqrt{3}}{2}}+\dfrac{\left(2-\sqrt{3}\right)\cdot\left(1+\sqrt{1-\dfrac{\sqrt{3}}{2}}\right)}{\sqrt{3}}\)
\(=\dfrac{1-\sqrt{1+\dfrac{\sqrt{3}}{2}}+\dfrac{\sqrt{3}-\sqrt{3+\dfrac{3\sqrt{3}}{2}}}{2}}{\sqrt{3}}+\dfrac{2+2\sqrt{1-\dfrac{\sqrt{3}}{2}}-\sqrt{3}-\sqrt{3-\dfrac{3\sqrt{3}}{2}}}{\sqrt{3}}\)
\(=\dfrac{-\left(2-2\sqrt{1+\dfrac{\sqrt{3}}{2}}+\sqrt{3}-\sqrt{3+\dfrac{3\sqrt{3}}{2}}\right)+2\cdot2\sqrt{1-\dfrac{\sqrt{3}}{2}}-\sqrt{3}-\sqrt{3-\dfrac{3\sqrt{2}}{2}}}{\sqrt{3}}\)
\(=1\)
Đúng 0
Bình luận (0)
Câu 1: Thực hiện phép tính:
a. \(\sqrt{3}\left(2\sqrt{6}-\sqrt{3}\right)-6\sqrt{2}\)
b. \(6\sqrt{12}-\sqrt{20}-2\sqrt{27}+\sqrt{125}\)
c. \(\sqrt{\left(1-\sqrt{3}\right)^2}-3\sqrt{\dfrac{1}{3}}\)
d. \(\dfrac{6}{\sqrt{6}}-\dfrac{5}{\sqrt{6}-1}\)
\(a,=6\sqrt{2}-3-6\sqrt{2}=-3\\ b,=12\sqrt{3}-2\sqrt{5}-6\sqrt{3}+5\sqrt{5}=6\sqrt{3}+3\sqrt{5}\\ c,=\sqrt{3}-1-\sqrt{3}=-1\\ d,=\sqrt{6}-\dfrac{5\left(\sqrt{6}+1\right)}{5}=\sqrt{6}-\sqrt{6}-1=-1\)
Đúng 0
Bình luận (0)