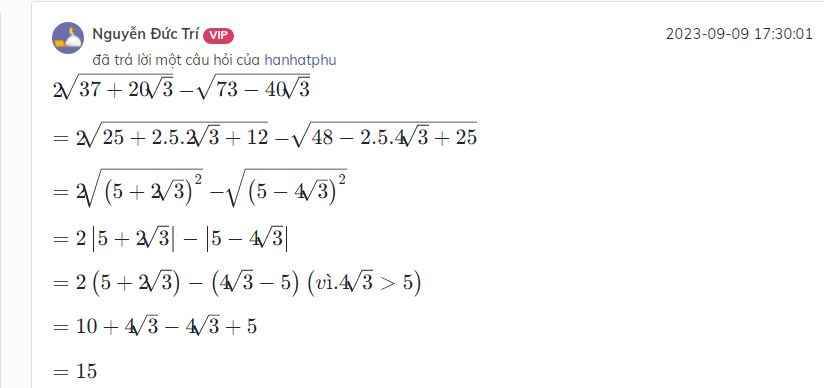Rút gọn \(M=\sqrt[2]{37+20\sqrt[2]{3}}-\sqrt[2]{37-20\sqrt[2]{3}}\)
NL
Những câu hỏi liên quan
Rút gọn biểu thức : A = \(\dfrac{1}{2-\sqrt{3}}\) + \(\dfrac{1}{2+\sqrt{3}}\) - \(\sqrt{37-20\sqrt{3}}\)
\(A=\dfrac{1}{2-\sqrt{3}}+\dfrac{1}{2+\sqrt{3}}-\sqrt{37-20\sqrt{3}}\)
\(=\dfrac{2+\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}+\dfrac{2-\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}-\sqrt{\left(5-2\sqrt{3}\right)^2}\)
\(=2+\sqrt{3}+2-\sqrt{3}-5+2\sqrt{3}\)
\(=2\sqrt{3}-1\)
Đúng 2
Bình luận (0)
Rút gọn biểu thức :
\(\sqrt{37-20\sqrt{3}}-\sqrt{37+20\sqrt{3}}\)
= \(\sqrt{12-2.2\sqrt{3}.5+25}-\sqrt{12+2.2\sqrt{3}.5+25}\)
= \(\sqrt{\left(2\sqrt{3}-5\right)^2}-\sqrt{\left(2\sqrt{3}+5\right)^2}\)
= \(|2\sqrt{3}-5|-2\sqrt{3}-5\)
=\(5-2\sqrt{3}-2\sqrt{3}-5=-4\sqrt{3}\)
Đúng 1
Bình luận (0)
bây giờ vẫn còn công chúa
Trả lời:
\(\sqrt{37-20\sqrt{3}}-\sqrt{37+20\sqrt{3}}\)
\(=\sqrt{25-20\sqrt{3}+12}-\sqrt{25+20\sqrt{3}+12}\)
\(=\sqrt{\left(5-2\sqrt{3}\right)^2}-\sqrt{\left(5+2\sqrt{3}\right)^2}\)
\(=5-2\sqrt{3}-5-2\sqrt{3}\)
\(=-4\sqrt{3}\)
1 . Rút gọn : \(\sqrt{37-20\sqrt{3}}+\sqrt{37+20\sqrt{3}}\)
2 . Cho a , b , c > 0 . CM : \(\frac{ab+bc+ca}{a^2+b^2+c^2}+\frac{\left(a+b+c\right)^2}{abc}\ge28\)
Bài 1 :
Ta có :
\(\sqrt{37-20\sqrt{3}}+\sqrt{37+20\sqrt{3}}=\sqrt{25-2.5.2\sqrt{3}+12}\)
\(+\sqrt{25+2.5.2\sqrt{3}+12}\)
\(=\sqrt{\left(5-2\sqrt{3}\right)^2}+\sqrt{\left(5+2\sqrt{3}\right)^2}\)
\(5-2\sqrt{3}+5+2\sqrt{3}\)
\(=5+5=10\)
Bài 2 :
Với x , y , z > 0 . Ta có :
+ ) \(\frac{x}{y}+\frac{y}{x}\ge2\left(1\right)\)
+ ) \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge\frac{9}{x+y+z}\left(2\right)\)
+ ) \(x^2+y^2+z^2\ge xy+yz+zx\Leftrightarrow\frac{x^2+y^2+z^2}{xy+yz+zx}\ge1\left(3\right)\)
Xảy ra đăng thức ở : \(\left(1\right),\left(2\right),\left(3\right)\Leftrightarrow x=y=z\) . Ta có :
\(P=\frac{ab+bc+ca}{a^2+b^2+c^2}+\left(a+b+c\right)^2.\frac{\left(a+b+c\right)}{abc}\)
\(=\frac{ab+bc+ca}{a^2+b^2+c^2}+\left(a^2+b^2+c^2+2ab+2bc+2ca\right).\frac{\left(a+b+c\right)}{abc}\)
Áp dụng các bất đẳng thức (1) , (2) , (3) ta được :
\(P\ge\frac{ab+bc+ca}{a^2+b^2+c^2}+\left(a^2+b^2+c^2\right).\frac{9}{ab+bc+ca}+2.9\)
\(=\left(\frac{ab+bc+ca}{a^2+b^2+c^2}+\frac{a^2+b^2+c^2}{ab+bc+ca}\right)+8.\frac{a^2+b^2+c^2}{ab+bc+ca}+18\)
\(\ge2+8+18=28\)
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}a^2+b^2+c^2=ab+bc+ca\\ab=bc=ca\end{cases}\Leftrightarrow a=b=c}\)
Rút gọn biểu thức :
\(\sqrt{37-20\sqrt{3}}-\sqrt{37+20\sqrt{3}}\)
\(=\sqrt{\left(5-2\sqrt{3}\right)^2}+\sqrt{\left(5+2\sqrt{3}\right)^2}\)
\(=\left|5-2\sqrt{3}\right|+\left|5+2\sqrt{3}\right|\)
\(=5-2\sqrt{3}+5+2\sqrt{3}\)
\(=10\)
Đúng 0
Bình luận (0)
\(2\sqrt{37+20\sqrt{3}}\) - \(\sqrt{73-40\sqrt{3}}\)
\(2\sqrt[]{37+20\sqrt[]{3}}-\sqrt[]{73-40\sqrt[]{3}}\)
\(=2\sqrt[]{25+2.5.2\sqrt[]{3}+12}-\sqrt[]{48-2.5.4\sqrt[]{3}+25}\)
\(=2\sqrt[]{\left(5+2\sqrt[]{3}\right)^2}-\sqrt[]{\left(5-4\sqrt[]{3}\right)^2}\)
\(=2\left|5+2\sqrt[]{3}\right|-\left|5-4\sqrt[]{3}\right|\)
\(=2\left(5+2\sqrt[]{3}\right)-\left(4\sqrt[]{3}-5\right)\left(vì.4\sqrt[]{3}>5\right)\)
\(=10+4\sqrt[]{3}-4\sqrt[]{3}+5\)
\(=15\)
Đúng 1
Bình luận (0)
Rút gọn biểu thức
a) \(\left(\sqrt{14}-3\sqrt{2}\right)^2+6\sqrt{28}\)
b) \(2\sqrt{20}-3\sqrt{20}+\sqrt{125}\)
`a)(\sqrt{14}-3\sqrt{2})^2+6\sqrt{28}`
`=14-12\sqrt{7}+18+12\sqrt{7}=32`
`b)2\sqrt{20}-3\sqrt{20}+\sqrt{125}`
`=4\sqrt{5}-6\sqrt{5}+5\sqrt{5}`
`=3\sqrt{5}`.
Đúng 1
Bình luận (0)
a) \(\left(\sqrt{14}-3\sqrt{2}\right)^2-6\sqrt{28}\)
\(=\left(\sqrt{14}\right)^2-2\cdot\sqrt{14}\cdot3\sqrt{2}+\left(3\sqrt{2}\right)^2+6\sqrt{28}\)
\(=14-6\sqrt{28}+18+6\sqrt{28}\)
\(=14+18\)
\(=32\)
b) \(2\sqrt{20}-3\sqrt{20}+\sqrt{125}\)
\(=2\cdot2\sqrt{5}-3\cdot2\sqrt{5}+5\sqrt{5}\)
\(=4\sqrt{5}-6\sqrt{5}+5\sqrt{5}\)
\(=3\sqrt{5}\)
Đúng 2
Bình luận (0)
\(2\sqrt{37+20\sqrt{3}}\) - \(\sqrt{73-40\sqrt{3}}\)
Lời giải tri tiết
Rút gọn biểu thức :
a) A=\(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\).
b)B=\(\sqrt[3]{20+14\sqrt{2}}+\sqrt[3]{20-14\sqrt{2}}\)
c) C=\(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}.\)
a) Ta có: \(A^3=\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right)^3\)
\(=2+\sqrt{5}+2-\sqrt{5}+3\cdot\sqrt[3]{\left(2+\sqrt{5}\right)\left(2-\sqrt{5}\right)}\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right)\)
\(=4-3\cdot A\)
\(\Leftrightarrow A^3+3A-4=0\)
\(\Leftrightarrow A^3-A+4A-4=0\)
\(\Leftrightarrow A\left(A-1\right)\left(A+1\right)+4\left(A-1\right)=0\)
\(\Leftrightarrow\left(A-1\right)\left(A^2+A+4\right)=0\)
\(\Leftrightarrow A=1\)
Đúng 3
Bình luận (0)
Rút gọn
\(A=\sqrt[3]{20+14\sqrt{2}}+\sqrt[3]{20-14\sqrt{2}}\)
\(A=\sqrt[3]{20+14\sqrt{2}}+\sqrt[3]{20-14\sqrt{2}}=\sqrt[3]{2^3+3.2^2.\sqrt{2}+3.2.\left(\sqrt{2}\right)^2+\left(\sqrt{2}\right)^3}+\sqrt[3]{2^3-3.2^2.\sqrt{2}+3.2.\left(\sqrt{2}\right)^2-\left(\sqrt{2}\right)^3}\)\(=\sqrt[3]{\left(2+\sqrt{2}\right)^3}+\sqrt[3]{\left(2-\sqrt{2}\right)^3}=2+\sqrt{2}+2-\sqrt{2}=4.\)
Đúng 0
Bình luận (0)