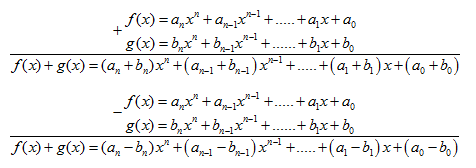Cho \(\left(1+2x\right)^n=a_0+a_1x+...+a_nx^n\) và \(a_0+a_1+...+a_n=729\). Tìm n và số hạng thứ 5
TD
Những câu hỏi liên quan
CMR: Không có đa thức f(x) nào mà: \(f\left(x\right)=a_nx^n+a_{n-1}x^{n-1}+.........+a_1x+a_0\left(a_1,a_2,a_3,............,a_n\in Z\right)\) có thể nhận giá trị f(7)=15 và f(15)=9
Ta có \(f\left(7\right)=15\Rightarrow f\left(7\right)-15=0\Rightarrow f\left(x\right)-15=P\left(x\right).\left(x-7\right)\)
\(\Rightarrow f\left(15\right)-15=P\left(x\right).8\Rightarrow-15=P\left(x\right).8\Rightarrow P\left(x\right)=\dfrac{-3}{4}\). (vô lí vì P(x) có các hệ số đều nguyên).
Vậy...
Đúng 1
Bình luận (0)
Gọi \(a_0;a_1;a_2;...;a_n\) là các hệ số của đa thức \(f\left(x\right)=a_0+a_1x+a_2x^2+...+a_nx^n\) .
Hãy tính tổng các hệ số của đa thức\(A\left(x\right)=\left(x+1\right)^{2012}\)
Cho đa thức Pleft(xright)a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0 với a_nne0. Giả sử alpha là nghiệm của P(x). Chứng minh rằng:a) left|alpharight| 1+maxleft|dfrac{a_i}{a_n}right|left(0le ile n-1right)b) left|alpharight|le2maxleft|dfrac{a_i}{a_n}right|left(0le ile n-1right)
Đọc tiếp
Cho đa thức \(P\left(x\right)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\) với \(a_n\ne0\). Giả sử \(\alpha\) là nghiệm của P(x). Chứng minh rằng:
a) \(\left|\alpha\right|< 1+max\left|\dfrac{a_i}{a_n}\right|\left(0\le i\le n-1\right)\)
b) \(\left|\alpha\right|\le2max\left|\dfrac{a_i}{a_n}\right|\left(0\le i\le n-1\right)\)
- Nếu \(a_i=0\) ; \(\forall i\in\left(0;n-1\right)\Rightarrow a_nx^n=0\Rightarrow\alpha=0< 1\) thỏa mãn
- Nếu tồn tại \(a_i\ne0\), đặt \(max\left|\dfrac{a_i}{a_n}\right|=A>0\)
Do \(\alpha\) là nghiệm nên:
\(a_n\alpha^n+a_{n-1}\alpha^{n-1}+...+a_1\alpha+a_0=0\)
\(\Leftrightarrow\dfrac{a_0}{a_n}+\dfrac{a_1}{a_n}\alpha+...+\dfrac{a_{n-1}}{a_n}\alpha^{n-1}=-\alpha^n\)
\(\Leftrightarrow\left|\alpha^n\right|=\left|\dfrac{a_0}{a_n}+\dfrac{a_1}{a_n}\alpha+...+\dfrac{a_{n-1}}{a_n}\alpha^{n-1}\right|\)
\(\Rightarrow\left|\alpha^n\right|\le\left|\dfrac{a_0}{a_n}\right|+\left|\dfrac{a_1}{a_n}\right|.\left|\alpha\right|+...+\left|\dfrac{a_{n-1}}{a_n}\right|.\left|\alpha^{n-1}\right|\le A+A.\left|\alpha\right|+...+A.\left|\alpha^{n-1}\right|\)
\(\Rightarrow\left|\alpha^n\right|\le A\left(1+\left|\alpha\right|+\left|\alpha^2\right|+...+\left|\alpha^{n-1}\right|\right)\)
\(\Rightarrow\left|\alpha^n\right|\le A.\dfrac{\left|\alpha^n\right|-1}{\left|\alpha\right|-1}\)
TH1: Nếu \(\left|\alpha\right|\le1\) hiển nhiên ta có \(\left|\alpha\right|< 1+A\) (đpcm)
TH2: Nếu \(\left|\alpha\right|>1\)
\(\Rightarrow\left|\alpha^n\right|\le\dfrac{A.\left|\alpha^n\right|}{\left|\alpha\right|-1}-\dfrac{A}{\left|\alpha\right|-1}< \dfrac{A.\left|\alpha^n\right|}{\left|\alpha\right|-1}\)
\(\Leftrightarrow\left|\alpha\right|-1< A\Rightarrow\left|\alpha\right|< 1+A\) (đpcm)
Đúng 1
Bình luận (0)
Cho khai triển
\(\left(1+2x\right)^{2023}=a_0+a_1x+a_2x^2+...+a_nx^2\).Tính tổng các hệ số trong khai triển ?
Tổng các hệ số trong khai triển là:
\(a_0+a_1+...+a_n=\left(1+2.1\right)^{2023}=3^{2023}\)
Đúng 0
Bình luận (0)
Cho biểu thức \(\left(3x^8-2x^6+2x^4-x^2+1\right)^5=a_0+a_1x+a_2x+...+a_{40}x\). Giá trị của tổng \(a_0+a_1+a_2+...+a_{40}=...\)
\(\left(3x^8-2x^6+x^5+2x^4-x^2+1\right)^5=a_0+a_1x+a_2x^2+...+a_{40}x^{40}\)
Giá trị của tổng: \(a_0+a_1+a_2+....+a_{40}=?\)
Ta có: \(\left(3x^8-2x^6+x^5+2x-x^2+1\right)^5=a_0+a_1x+...+a_{40}x^{40}\)
Từ khai triển này ta thay x = 1 vào thì được
\(a_0+a_1+...+a_{40}=\left(3-2+1+2-1+1\right)^5=4^5=1024\)
Đúng 0
Bình luận (0)
Anh xin trả lời câu của bạn ngonhuminh:
\(a_0+a_1+...+a_{40}=P\left(1\right)=1024\)
\(a_0-a_1+a_2-...+a_{40}=P\left(-1\right)=32\)
Trừ 2 điều trên cho nhau vế theo vế rồi chia 2 được:
\(a_1+a_3+...+a_{39}=\frac{1024+32}{2}=528\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Xét dãy số: ...,\(a_{-3},a_{-2},a_{-1},a_0,a_1,a_2,a_3,...\), được định nghĩa bởi
\(a_n-\left(n+1\right)\times a_{n-2}=\left(n+3\right)^2\)với mọi số nguyên n. Tính \(a_0\)
Cho các đa thức :
\(f\left(x\right)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\)
\(g\left(x\right)=b_nx^n+b_{n-1}x^{n-1}+...+b_1x+b_0\)
a)Tính f(x)+g(x)
b)Tính f(x)-g(x)
Cho các đa thức :
\(f\left(x\right)=a_nx^n+a_{n-1}x^{n-1}+....+a_1x+a_0\)
\(g\left(x\right)=b_nx^n+b_{n-1}x^{n-1}+....+b_1x+b_0\)
a) Tính \(f\left(x\right)+g\left(x\right)\)
b) Tính \(f\left(x\right)-g\left(x\right)\)
a. Ta có: f(x) + h(x) = g(x)
Suy ra: h(x) = g(x) – f(x) = (x4 – x3 + x2 + 5) – (x4 – 3x2 + x – 1)
= x4 – x3 + x2 + 5 – x4 + 3x2 – x + 1
= -x3 + 4x2 – x + 6
b. Ta có: f(x) – h(x) = g(x)
Suy ra: h(x) = f(x) – g(x) = (x4 – 3x2 + x – 1) – (x4 – x3 + x2 + 5)
= x4 – 3x2 + x – 1 – x4 + x3 – x2 – 5
= x3 – 4x2 + x – 6
Đúng 0
Bình luận (0)