Câu 8. Tọa độ giao điểm của đồ thị của hàm số f(x) = -2x và g(x) = 3x - 5 là:
A. (1; -2) B. (-1;-2) C. (1;2) D. (-1;2)
CN
Những câu hỏi liên quan
Tọa độ giao điểm của đồ thị của hàm số f(x) = -2x và g(x) = 3x - 5 là:
A. (1; -2) B. (-1;-2) C. (1;2) D. (-1;2)
Cho các hàm số y=f(x)=2x+a và y=g(x)=3x+b
a) Vẽ đồ thị của hai đồ thị trên
b) Xác định giao điểm và biểu diễn giao điểm đó trên trục tọa độ
cho hàm số y=-2x+1a)Xác định tọa độ giao điểm của đồ thị hàm số trên và Ox,Oy
b)CMR:f(x1)+f(x2)=f(x1+x2)+1
c)Tìm tọa độ giao điểm của đồ thị hàm số trên và đồ thị hàm số y=|x|
a) Tọa độ giao điểm của đồ thị hàm số y=-2x+1 với trục Ox là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}y=-2x+1\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+1=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x=-1\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=0\end{matrix}\right.\)
Tọa độ giao điểm của đồ thị hàm số y=-2x+1 với trục Oy là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}x=0\\y=-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hai hàm số f(x)=2x-1 và g(x)=4-x. Không về đô thị của chúng, tính tọa độ giao điểm của hai đồ thị trên.
Câu 2: Cho hàm số yfleft(xright)dfrac{1}{2}x^2 có đồ thị là (P)a) Tính f(-2)b) Vẽ đồ thị (P) trên mặt phẳng với hệ trục tọa độ Oxyc) Cho hàm số y 2x + 6 (d). Tìm tọa độ giao điểm của hai đồ thị (P) và (d)Câu 3: Cho x1,x2 là hai nghiệm của phương trình x2 - 2x - 1 0Tính giá trị của biểu thức P (x1)3 + (x2)3
Đọc tiếp
Câu 2: Cho hàm số \(y=f\left(x\right)=\dfrac{1}{2}x^2\) có đồ thị là (P)
a) Tính f(-2)
b) Vẽ đồ thị (P) trên mặt phẳng với hệ trục tọa độ Oxy
c) Cho hàm số y = 2x + 6 (d). Tìm tọa độ giao điểm của hai đồ thị (P) và (d)
Câu 3: Cho x1,x2 là hai nghiệm của phương trình x2 - 2x - 1 = 0
Tính giá trị của biểu thức P = (x1)3 + (x2)3
Câu 2:
c) Phương trình hoành độ giao điểm của (P) và (d) là:
\(\dfrac{1}{2}x^2=2x+6\)
\(\Leftrightarrow\dfrac{1}{2}x^2-2x-6=0\)
\(\Leftrightarrow x^2-4x-12=0\)
\(\Leftrightarrow x^2-4x+4=16\)
\(\Leftrightarrow\left(x-2\right)^2=16\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=4\\x-2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
Thay x=6 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot6^2=18\)
Thay x=-2 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot\left(-2\right)^2=\dfrac{1}{2}\cdot4=2\)
Vậy: Tọa độ giao điểm của (P) và (d) là (6;18) và (-2;2)
Đúng 0
Bình luận (0)
Câu 3:
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-2\right)}{1}=2\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{-1}{1}=-1\end{matrix}\right.\)
Ta có: \(P=x_1^3+x_2^3\)
\(=\left(x_1+x_2\right)^3-3\cdot x_1x_2\left(x_1+x_2\right)\)
\(=2^3-3\cdot\left(-1\right)\cdot2\)
\(=8+3\cdot2\)
\(=8+6=14\)
Vậy: P=14
Đúng 0
Bình luận (0)
a, \(f\left(-2\right)=\dfrac{1}{2}.\left(-2\right)^2=\dfrac{1}{2}.4=2\)
b,
c, Tọa độ giao điểm của 2 đồ thị (P) và (d) thỏa mãn phương trình
\(2x+6=\dfrac{1}{2}x^2\Leftrightarrow x=6;x=-2\)
TH1 : Thay x = 6 vào f(x) ta được : \(\dfrac{1}{2}.6^2=18\)
TH2 : Thay x = -2 vào f(x) ta được : \(\dfrac{1}{2}.\left(-2\right)^2=2\)
Vậy tọa độ giao điểm của (P) và (d) là \(\left(6;18\right);\left(-2;2\right)\)
Đúng 0
Bình luận (0)
cho các hàm số y=f(x)=2x và y=g(x)=18/x. Không vẽ đồ thị của chúng hãy tính tọa độ giao điểm của 2 đồ thị
Cho các hàm số y = f(x)=2x và y =g(x)=18/x.Tính tọa độ giao điểm của 2 đồ thị
Cho hàm số y = f(x) = 2x và hàm số y = g(x) = - 3x. Xác định tọa độ điểm A trên đồ thị f(x) và tọa độ điểm B trên đồ thị g(x) biết chúng cùng có hoành độ bằng ( - 1). Tính diện tích tam giác OAB (với O là gốc toạ độ).
giúp mình gấp mình tick cho
a vẽ đồ thị hàm số : y= / 2x+1/
b xác định tọa độ giao điểm của đồ thị hàm số ở câu a với đồ thị hầm số y= 3x-5
a.
* Vẽ hệ tọa độ Oxy
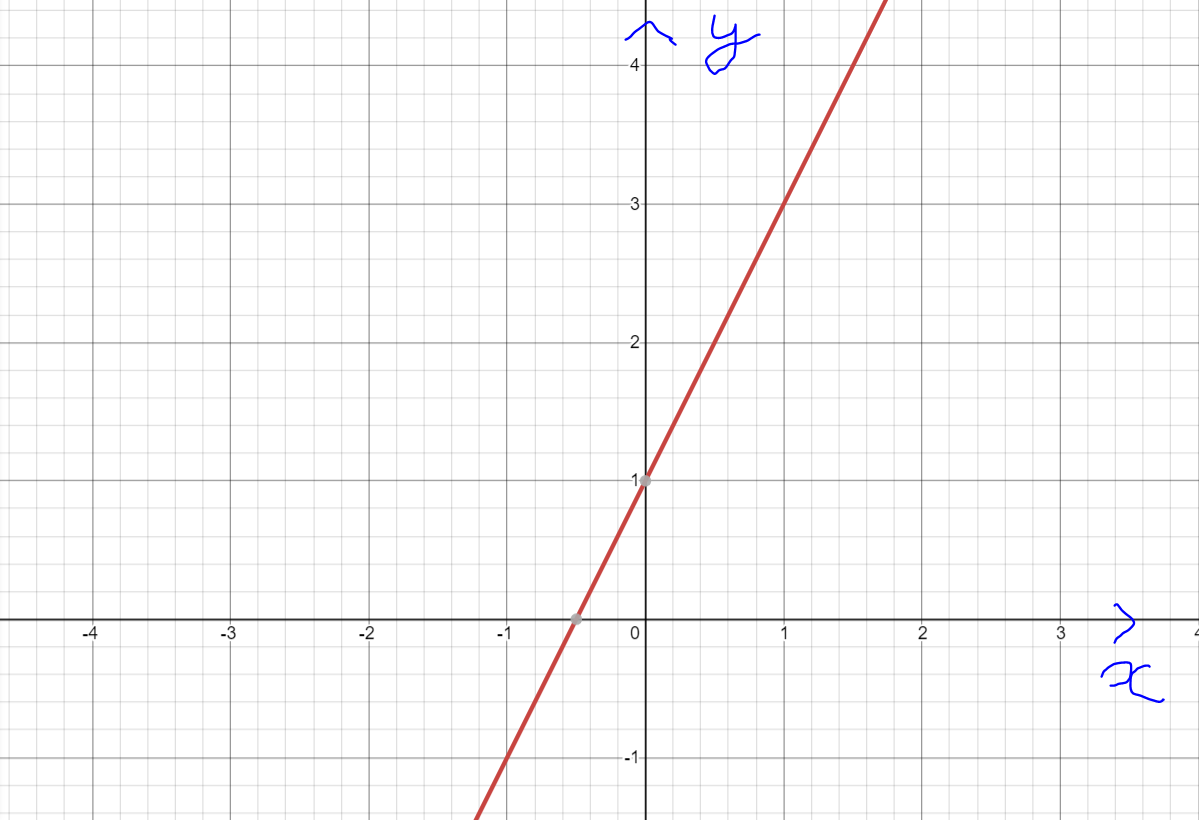
* Vẽ đồ thị hàm số y = 2x+1
| x | 0 | -1/2 |
| y | 1 | 0 |
=> Đồ thị hàm số y=2x+1 là một đường thẳng cắt trục hoành tại điểm có tọa độ (-1/2;0) và cắt trục tung tại điểm có tọa độ (0;1)
b.
Xét phương trình hoành độ giao điểm của y=2x+1 và y=3x-5:
2x + 1 = 3x - 5
=> -x = -6 => x = 6
Thay x = 6 vào y=2x+1 => y = 2*6 + 1 => y = 13
=> Tọa độ giao điểm của đồ thị hàm số y=2x+1 và đồ thị hàm số y=3x-5 là (6;13)
Đúng 0
Bình luận (0)



