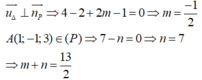trong mp Oxy,tìm điểm A nằm trên đường thẳng Δ:x+2y-1=0 và cách M(-1;-2) một khoảng cách bằng 2\(\sqrt{2}\)
NL
Những câu hỏi liên quan
Trong mp Oxy cho đường thẳng (d): x – 2y – 3 0. Viết phương trình (d1) là ảnh của (d) qua phép đối xứng qua
Δ
:
x
+
1
0
A.
−
7
2
x
+
y
−
11
2
0
B.
7
x
+
y
+
11
0
C.
7
2
x
+
y...
Đọc tiếp
Trong mp Oxy cho đường thẳng (d): x – 2y – 3 = 0. Viết phương trình (d1) là ảnh của (d) qua phép đối xứng qua Δ : x + 1 = 0
A. − 7 2 x + y − 11 2 = 0
B. 7 x + y + 11 = 0
C. 7 2 x + y + 11 2 = 0
D. − 7 x + y − 11 = 0
Đáp án C
d ∩ Δ = O ( − 1 ; − 2 )
Chọn A(1;5) ∈ d
Gọi A’ là điểm đối xứng với A qua Δ : x + 1 = 0
Đường thẳng d’đi qua A và vuông góc với Δ có phương trình: − ( y − 5 ) = 0
d’: − y + 5 = 0
d ' ∩ Δ = I ( − 1 ; 5 ) =>I là trung điểm của AA’
Đ △ : A-> A’(–3;5)
Phương trình đường thẳng (d1) đi qua O; A’: 7 2 x + y + 11 2 = 0
Đúng 0
Bình luận (0)
Trong mp Oxy, cho hai điểm A(-2;1),B(2;3) và đường thẳngv:x-2y-1=0. Viết phương trình đường tròn có tâm I nằm trên đường thăng :x-2y-1=0, đi qua A, B
Lời giải:
Do $I\in (x-2y-1=0)$ nên gọi tọa độ của $I$ là $(2a+1,a)$
Đường tròn đi qua 2 điểm $A,B$ nên: $IA^2=IB^2=R^2$
$\Leftrightarrow (2a+1+2)^2+(a-1)^2=(2a+1-2)^2+(a-3)^2=R^2$
$\Rightarrow a=0$ và $R^2=10$
Vậy PTĐTr là: $(x-1)^2+y^2=10$
Đúng 1
Bình luận (0)
Giả sử \(I=\left(2m+1;m\right)\)
Ta có: \(IA=IB\)
\(\Leftrightarrow\sqrt{\left(-2-2m-1\right)^2+\left(1-m\right)^2}=\sqrt{\left(2-2m-1\right)^2+\left(3-m\right)^2}\)
\(\Leftrightarrow4m^2+9+12m+m^2-2m+1=4m^2-4m+1+m^2-6m+9\)
\(\Leftrightarrow5m^2+10m+10=5m^2-10m+10\)
\(\Leftrightarrow m=0\)
\(\Rightarrow I=\left(1;0\right)\)
Bán kính \(R=\sqrt{\left(2-1\right)^2+3^2}=\sqrt{10}\)
Phương trình đường tròn: \(\left(x-1\right)^2+y^2=10\)
Đúng 1
Bình luận (0)
Trong mặt phẳng Oxy, cho đường thẳng d: \(2x+y-3=0\) và đường thẳng Δ:\(4x+2y-1=0\). Tập hợp các điểm cách đều đường thẳng d và Δ nằm trên đường thẳng l có phương trình \(ax+by+1=0\) với a, b ∈ R. Tính a+b
Ta có : Đường thẳng I cách đều 2 đường thẳng d và denta
\(\Rightarrow\dfrac{\left|2x+y-3\right|}{\sqrt{5}}=\dfrac{\left|4x+2y-1\right|}{2\sqrt{5}}\)
\(\Rightarrow2\left|2x+y-3\right|=\left|4x+2y-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+2y-6=4x+2y-1\\4x+2y-6=-4x-2y+1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-6=1\left(L\right)\\8x+4y-7=0\end{matrix}\right.\)
\(\Leftrightarrow-\dfrac{8}{7}+\left(-\dfrac{4}{7}\right)+1=0\)
\(\Rightarrow a+b=-\dfrac{8}{7}-\dfrac{4}{7}=-\dfrac{12}{7}\)
Vậy ..
Đúng 0
Bình luận (0)
Trong mp Oxy cho đường thẳng (P): x-2y+3=0, A(1,3), B(-1,-1). Tìm điểm M thuộc d thõa P= MA+MB là nhỏ nhất
Đường thẳng đi qua hai điểm A và B nhận \(\overrightarrow{AB}=\left(-2;-4\right)\) làm vecto chỉ phương.
Phương trình đường thẳng AB là \(\dfrac{x-1}{-2}=\dfrac{y-3}{-4}\Leftrightarrow2x-y+1=0\)
\(P=MA+MB\) đạt giá trị nhỏ nhất khi M, A, B thẳng hàng
\(\Leftrightarrow M\) là giao điểm của đường thẳng AB và d
\(\Leftrightarrow M\) có tọa độ nghiệm của hệ \(\left\{{}\begin{matrix}x-2y+3=0\\2x-y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow M\left(\dfrac{1}{3};\dfrac{5}{3}\right)\)
Đúng 1
Bình luận (0)
Trong mp Oxy cho tam giác ABC có A (2;-4) B (0-2) và điểm C nằm trên đường thẳng d: 3x-y+1=0; diện tích tam giác ABC=1. Tìm tọa độ điểm C
trong mặt phẳng tọa độ Oxy cho điểm E(3;4), đường thẳng d : x + y - 1 0 và đường tròn (C) : x2 + y2 + 4x - 2y - 4 0 . Gọi M (m;1-m) là điểm nằm trên đường thẳng d và nằm ngoài đường tròn (C), từ M kẻ các tiếp tuyến MA, MB tới đường tròn (C), với A,B là các tiếp điểm. Gọi (E) là đường tròn tâm E và tiếp xúc với đường thẳng AB. Khi đường tròn (E) có chu vi lớn nhất. Tìm tọa độ điểm M
Đọc tiếp
trong mặt phẳng tọa độ Oxy cho điểm E(3;4), đường thẳng d : x + y - 1 = 0 và đường tròn (C) : x2 + y2 + 4x - 2y - 4 = 0 . Gọi M (m;1-m) là điểm nằm trên đường thẳng d và nằm ngoài đường tròn (C), từ M kẻ các tiếp tuyến MA, MB tới đường tròn (C), với A,B là các tiếp điểm. Gọi (E) là đường tròn tâm E và tiếp xúc với đường thẳng AB. Khi đường tròn (E) có chu vi lớn nhất. Tìm tọa độ điểm M
(C): x^2+y^2+4x-2y-4=0
=>(x+2)^2+(y-1)^2=9
=>I(-2;1); R=3
M thuộc d nên M(a;1-a)
M nằm ngoài (C) nên IM>R
=>IM^2>9
=>2a^2+4a-5>0
MA^2=MB^2=IM^2-IA^2=(a+2)^2+(-a)^2-9=2a^2+4a-5
=>x^2+y^2-2ax+2(a-1)y-6a+6=0(1)
A,B thuộc (C)
=>Tọa độ A,B thỏa mãn phương trình:
x^2+y^2+4x-2y-4=0(2)
(1)-(2)=(a+2)x-ay+3a-5=0(3)
Tọa độ A,B thỏa mãn (3) nên (3) chính là phương trình đường thẳng AB
(E) tiếp xúc AB nên (E): R1=d(E,AB)
Chu vi của (E) lớn nhất khi R1 lớn nhất
=>d(E;AB) lớn nhất
Gọi H là hình chiếu vuông góc của E lên AB
=>d(E,Δ)=EH<=EK=căn 10/2
Dấu = xảy ra khi H trùng K
=>AB vuông góc EK
vecto EK=(-1/2;3/2), AB có VTCP là (a;a+2)
AB vuông góc EK
=>-1/2a+3/2(a+2)=0
=>a=-3
=>M(-3;4)
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ trục toạ độ Oxy,cho hai điểm A(1;1),B(-4;3) và đường thẳng d:x-2y-1=0.Tìm điểm M thuộc d có toạ độ nguyên sao cho khoảng cách từ M đến đường thẳng AB bằng 6
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng
P
:
2
x
−
2
y
+
z
−
n
0
và đường thẳng
Δ
:
x
−
1
2
y
+
1
1
z
−...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng P : 2 x − 2 y + z − n = 0 và đường thẳng Δ : x − 1 2 = y + 1 1 = z − 3 2 m − 1 . Biết đường thẳng ∆ nằm trong mặt phẳng (P). Tổng m + n gần giá trị nào nhất sau đây?
A. 3
B. 4
C. 5
D. 6
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
P
:
2
x
−
2
y
+
z
−
n
0
và đường thẳng
Δ
:
x
−
1
2
y
+
1
1
z
−...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x − 2 y + z − n = 0 và đường thẳng Δ : x − 1 2 = y + 1 1 = z − 3 2 m − 1 . Biết đường thẳng ∆ nằm trong mặt phẳng (P). Tổng m + n gần giá trị nào sau đây nhất?
A. 3.
B. 4.
C. 5.
D. 6.