Chứng minh phương trình sau có ít nhất một nghiệm : \(2x^3-10x-7=0\)
NT
Những câu hỏi liên quan
Bài 3: a) CMR phương trình sau có ít nhất hai nghiệm:
b) CMR phương trình sau có ít nhất một nghiệm âm:
c) Chứng minh phương trình có ít nhất một nghiệm .
giúp em với ạ
Đọc tiếp
Bài 3: a) CMR phương trình sau có ít nhất hai nghiệm:
b) CMR phương trình sau có ít nhất một nghiệm âm:
c) Chứng minh phương trình có ít nhất một nghiệm .
giúp em với ạ
Chứng minh phương trình: \(\left|x\right|^3-2x^2+mx-1=0\) luôn có ít nhất 2 nghiệm phân biệt.
Chứng minh phương trình \(3x^4-3x^3-5x^2+2x+2=0\) có ít nhất 2 nghiệm nằm trong khoảng (-1;1)
Đặt \(f\left(x\right)=3x^4-3x^3-5x^2+2x+2\)
Hiển nhiên \(f\left(x\right)\) liên tục trên R cũng như mọi khoảng con của nó
\(f\left(-1\right)=1>0\)
\(f\left(-\dfrac{3}{4}\right)=-\dfrac{25}{256}< 0\)
\(f\left(0\right)=2>0\)
\(\Rightarrow\left\{{}\begin{matrix}f\left(-1\right).f\left(-\dfrac{3}{4}\right)< 0\\f\left(-\dfrac{3}{4}\right).f\left(0\right)< 0\end{matrix}\right.\) \(\Rightarrow f\left(x\right)\) có ít nhất 2 nghiệm thuộc (-1;0) nên có ít nhất 2 nghiệm thuộc (-1;1)
Đúng 0
Bình luận (0)
chứng minh rằng phương trình (m²-m+1)x⁴-2x³-1=0 có ít nhất 2 nghiệm /(-5;5)
Đặt \(f\left(x\right)=\left(m^2-m+1\right)x^4-3x^3-1\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên mọi khoảng trên R
\(f\left(0\right)=-1< 0\)
\(f\left(3\right)=81\left(m^2-m+1\right)-55=81\left(m-\dfrac{1}{2}\right)^2+\dfrac{23}{4}>0\)
\(\Rightarrow f\left(0\right).f\left(3\right)< 0\Rightarrow\) pt có ít nhất 1 nghiệm thuộc \(\left(0;3\right)\)
\(f\left(-1\right)=m^2-m+2=\left(m-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
\(\Rightarrow f\left(-1\right).f\left(0\right)< 0\Rightarrow\) pt có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)
\(\Rightarrow\) Pt có ít nhất 2 nghiệm thuộc \(\left(-1;3\right)\Rightarrow\) có ít nhất 2 nghiệm trên \(\left(-5;5\right)\)
Đúng 2
Bình luận (0)
Chứng minh rằng phương trình:
a) 2x3 + 6x + 1 = 0 có ít nhất hai nghiệm;
b) cosx = x có nghiệm.
a) Hàm số f(x) = 2x3 + 6x + 1 là hàm đa thức nên liên tục trên R.
Mặt khác vì f(0).f(1) = 1.(-3) < 0 nên phương trình có nghiệm trong khoảng (1; 2).
Vậy phương trình f(x) = 0 có ít nhất hai nghiệm.
b) Hàm số g(x) = cosx - x xác định trên R nên liên tục trên R.
Mặt khác, ta có g(0).g() = 1. (-
) < 0 nên phương trình đã cho có nghiệm trong khoảng (0;
).
Đúng 0
Bình luận (0)
Hoàng anh gia lai và Võ Đong Anh Tuấn chắc chắn là 1 người
Đúng 0
Bình luận (0)
ủa đâu có ???????
Một người là sao
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho phương trình x²+ax-b=0 có ít nhất một nghiệm thuộc khoảng (0;1). Chứng minh phương trình x²-2ax+b=0 có hai nghiệm phân biệt cùng dấu.
Đề bài sai, ví dụ: với \(a=b=1\) thì \(x^2+x-1=0\) có 1 nghiệm thuộc \(\left(0;1\right)\) thỏa mãn yêu cầu
Nhưng \(x^2-2x+1=0\) có nghiệm kép, không phải hai nghiệm phân biệt
Đúng 0
Bình luận (0)
Chứng minh rằng phương trình sau có ít nhất hai nghiệm: 2 x 3 - 5 x 2 + x + 1 = 0
Chứng minh rằng phương trình sau có ít nhất hai nghiệm :
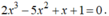
- Xét hàm số: f ( x ) = 2 x 3 - 5 x 2 + x + 1 là hàm đa thức.
⇒ Hàm số f liên tục trên R.
- Ta có:
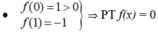 có ít nhất một nghiệm c1 ∈ (0;1).
có ít nhất một nghiệm c1 ∈ (0;1).
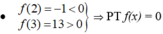 có ít nhất một nghiệm c2 ∈ (2;3).
có ít nhất một nghiệm c2 ∈ (2;3).
- Mà c ≠ c 2 nên PT f(x) = 0 có ít nhất 2 nghiệm.
Đúng 0
Bình luận (0)
Cho a,b,c là các số thực dương phân biệt có tổng bằng 3. Chứng minh rằng trong ba phương trình \(x^2-2ax+b=0;x^2-2bx+c;x^2-2cx+a=0\)
có ít nhất một phương trình có hai nghiệm phân biệt và ít nhất một phương trình vô nghiệm
* Giả sử cả 3 pt đều có nghiệm kép hoặc vô nghiệm ta có :
pt \(x^2-2ax+b=0\) (1) có \(\Delta_1'=\left(-a\right)^2-b=a^2-b\le0\)
pt \(x^2-2bx+c=0\) (2) có \(\Delta_2'=\left(-b\right)^2-c=b^2-c\le0\)
pt \(x^2-2cx+a=0\) (3) có \(\Delta_3'=\left(-c\right)^2-a=c^2-a\le0\)
\(\Rightarrow\)\(\Delta_1'+\Delta_2'+\Delta_3'=\left(a^2+b^2+c^2\right)-\left(a+b+c\right)\le0\) (*)
Lại có : \(0< a,b,c< 3\)\(\Rightarrow\)\(\hept{\begin{cases}a\left(3-a\right)>0\\b\left(3-b\right)>0\\c\left(3-c\right)>0\end{cases}\Leftrightarrow\hept{\begin{cases}3a>a^2\\3b>b^2\\3c>c^2\end{cases}}}\)
\(\Rightarrow\)\(\left(a^2+b^2+c^2\right)-\left(a+b+c\right)< 3\left(a+b+c\right)-\left(a+b+c\right)=2\left(a+b+c\right)=6>0\)
trái với (*)
Vậy có ít nhất một phương trình có hai nghiệm phân biệt
cái kia chưa bt làm -_-
Đúng 1
Bình luận (0)
nhầm r >_< sửa lại chỗ này nhé
Lại có : \(0< a,b,c< 3\)\(\Rightarrow\)\(\hept{\begin{cases}a\left(3-a\right)< 0\\b\left(3-b\right)< 0\\c\left(3-c\right)< 0\end{cases}\Leftrightarrow\hept{\begin{cases}3a< a^2\\3b< b^2\\3c< c^2\end{cases}}}\)
\(\Rightarrow\)\(\left(a^2+b^2+c^2\right)-\left(a+b+c\right)>3\left(a+b+c\right)-\left(a+b+c\right)=6>0\) :))
Đúng 1
Bình luận (0)
nếu a, b là các số dương hãy chứng minh phương trình \(\dfrac{a}{x^3+2x-1}+\dfrac{b}{x^3+x-2}=0\) có ít nhất 1 nghiệm nằm trong khoảng (-1;1)


