Chứng minh rằng với mọi giá trị của x ta luôn có:
2x4 + 1 ≤ 2x3 + x2
SD
Những câu hỏi liên quan
H24
21 tháng 4 2022 lúc 10:19
Chứng mình đa thức B(x) = 5x3 + 2x4 - x2 + 3x2 - x3 - x4 + 1 - 4x3 luôn nhận giá trị dương với mọi giá trị của biến x
Với x R. Chứng minh rằng: 2x4 + 1 >= 2x3 + x2
một đề bài lố bịch, một câu tl ngớ ngẩn, thế này mà olm có câu:
không có học trò dốt
mà chỉ có thầy chưa giỏi
em xin đổi lại là:
95% hs k biêt hoc toán
95% thầy cô trẻ dạy toán, rất giỏi toán
( vì điểm thi đh ở đhsp ngành toán lấy rất cao,em chỉ nói lên sự thật mong olm đừng trừ điểm)
Đúng 0
Bình luận (0)
Đề bài chính xác là CMR : 2x4 + 1 > 2x3 + 2x2 với mọi x thuộc R
\(\Leftrightarrow2x^4-2x^3-x^2+1\ge0\)
\(\Leftrightarrow2x^3\left(x-1\right)-\left(x-1\right)\left(x+1\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2x^3-x-1\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(x^3-x+x^3-1\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left[x\left(x^2-1\right)+\left(x-1\right)\left(x^2+x+1\right)\right]\ge0\)
\(\Leftrightarrow\left(x-1\right)^2\left[\left(x\left(x+1\right)+x+1\right)\right]\ge0\)
\(\Leftrightarrow\left(x-1\right)^2\left(2x^2+2x+1\right)\ge0\)
Có \(\left(x-1\right)^2\ge0\forall x\in R\)
\(2x^2+2x+1=x^2+x^2+2x+1=x^2+\left(x+1\right)^2\ge0\)
(đpcm)
cho 2 đa thức sau:
P(x)=2x3-x4+1+2x2+5x4-x3;
Q(x)=-3x4-1+5x3-x2-6x2-4x3
a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm của biến?
b) Tính P(-2)?
c) Tính P(x)+Q(x)?
d) Chứng minh rằng với mọi giá trị của x thì Q(x)-P(x) luôn nhận giá trị âm.
cho 2 đa thức sau:
P(x)=2x3-x4+1+2x2+5x4-x3;
Q(x)=-3x4-1+5x3-x2-6x2-4x3
a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm của biến?
b) Tính P(-2)?
c) Tính P(x)+Q(x)?
d) Chứng minh rằng với mọi giá trị của x thì Q(x)-P(x) luôn nhận giá trị âm.
Cho biểu thức:
P = 2 x 4 - 1 - 1 1 - x 2
a) Tìm điều kiện xác định của biểu thức P.
b) Chứng minh giá trị của P luôn âm với x ≠ ±1
a) Ta có: x4 - 1 = (x2 + 1)(x2-1), trong đó : x2 + 1 > 0, với mọi x.
Vậy điều kiện : x2 – 1 ≠ 0
x2 – 1 = (x – 1)(x + 1) ≠ 0 ⇒ x ≠ ±1
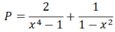
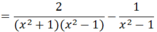
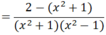
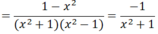
Do x2 + 1 > 0 với mọi x nên P < 0 với mọi x ≠ ±1
Đúng 0
Bình luận (0)
Cho hàm số: y = x 3 − (m + 4) x 2 − 4x + m (1). Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.
y′ = 3 x 2 − 2(m + 4)x – 4
∆ ′ = m + 4 2 + 12
Vì ∆ ’ > 0 với mọi m nên y’ = 0 luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó). Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.
Đúng 0
Bình luận (0)
Cho phương trình: x² - mx + m - 1 = 0(x là ẩn) a) Chứng minh rằng phương trình luôn có nghiệm với mọi giá trị của m b) Tìm giá trị của m để phương trình có 2 nghiệm x1, x2 thoả mãn: x1 - 2x2 = 1
cho biểu thức A = ( x - 3 ) ( x2 + 3x + 9 ) - ( x - 1 )3 + 4 ( x + 2 ) ( 2 - x ) - x
a. Chứng minh A = - x2 - 4x - 10
b. Chứng minh A luôn có giá trị âm với mọi giá trị của số thực x
a: \(A=x^3-27-x^3+3x^2-3x+1-4\left(x^2-4\right)-x\)
\(=3x^2-4x-26-4x^2+16\)
\(=-x^2-4x-10\)
Đúng 0
Bình luận (0)
Cho phương trình X^2 - 2(m + 1)x + m - 6 = 0 (1) , ( với m là tham số )
a> Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt x1; x2 với mọi giá trị của m
b> Tìm một hệ thức liên hệ giữa x1 ; x2 không phụ thuộc vào m
c> với giá trị nào của m thì phương trình (1) có ít nhất một nghiệm dương
a: Δ=(2m+2)^2-4(m-6)
=4m^2+8m+4-4m+24
=4m^2+4m+28
=(2m+1)^2+27>0
=>Phương trình luôn có hai nghiệm phân biệt
c: Để (1) có ít nhất 1 nghiệm dương thì
m-6<0 hoặc (2m+2>0 và m-6>0)
=>m>6 hoặc m<6
Đúng 0
Bình luận (0)
a)Chứng minh thuoqng của phép chia sau luôn có giá trị dương:
(x4-2x3+6x2+x+14):(x2-3x+7)
b)Cho x+y=1.Tính giá trị biểu thức A=x3+3xy+y3
\(a,x^4-2x^3+6x^2+x+14\\ =\left(x^4-3x^3+7x^2\right)+\left(x^3-3x^2+7x\right)+\left(2x^2-6x+14\right)\\ =\left(x^2-3x+7\right)\left(x^2+x+2\right):\left(x^2-3x+7\right)=x^2+x+2\)
Ta có \(x^2+x+2=x^2+x+\dfrac{1}{4}+\dfrac{7}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}>0\)
Vậy ...
\(b,A=x^3+3xy+y^3\\ A=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\\ A=x^2-xy+y^2+3xy\\ A=x^2+2xy+y^2=\left(x+y\right)^2=1\)
Đúng 5
Bình luận (0)