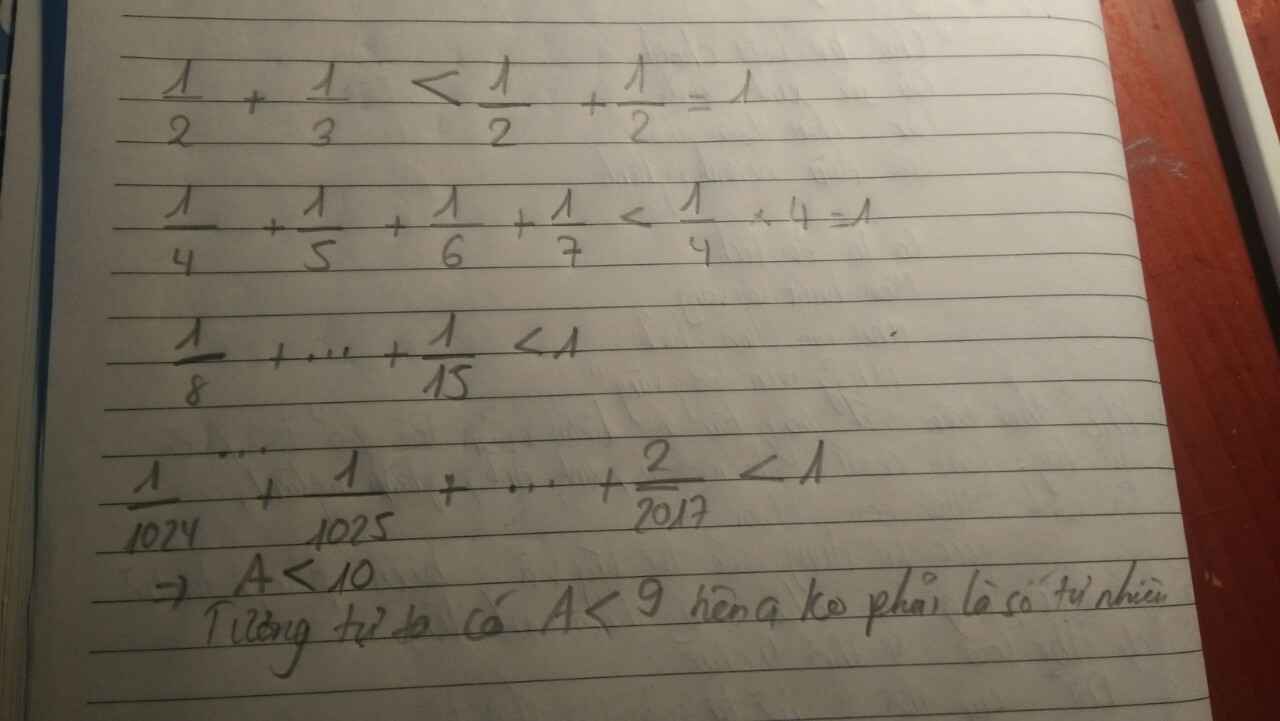cho \(A=\dfrac{a^3}{24}+\dfrac{a^2}{8}+\dfrac{a}{12}\)với a là số tự nhiên. Chứng tỏ A∈Z
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PA
Những câu hỏi liên quan
Cho A = \(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2017}\). Chứng tỏ rằng A không phải là số tự nhiên.
Cho A = \(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2017}\). Chứng tỏ rằng A không phải là số tự nhiên.
Cho a,b,c là các số tự nhiên khác 0. Chứng tỏ: \(\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}\)không phải là số tự nhiên.
Với a,b,c dương, ta có:
a/a+b > a/a+b+c
b/b+c > b/a+b+c
c/c+a > c/a+b+c
=> A > a/a+b+c + b/a+b+c + c/a+b+c => A>1. (1)
Ta lại có
A = a/a+b + b/b+c + c/c+a
= a+b-b/a+b + b+c-c/b+c + c+a-a/c+a
= 1-b/a+b + 1-c/b+c + 1-a/c+a
= 3-(b/a+b + c/b+c + a/c+a) = 3-B
Tương tự phần chứng minh trên, ta có
b/a+b > b/a+b+c
c/b+c > c/a+b+c
a/a+c > a/a+b+c
=> B > b/a+b+c + c/a+b+c + a/a+b+c => B>1
mà A = 3-B
=> A < 2 (2)
Từ (1) và (2) => 1<A<2
Mà không có số tự nhiên nào ở giữa 1 và 2 => A không là số tự nhiên
Đúng 0
Bình luận (0)
a) Tìm số tự nhiên n biết:
\(\dfrac{4}{3\cdot5}+\dfrac{8}{5\cdot9}+\dfrac{12}{9\cdot15}+....+\dfrac{32}{n\cdot\left(n+16\right)}=\dfrac{16}{25}\)
b) Chứng tỏ rằng:
\(\dfrac{2018}{2019}+\dfrac{2019}{2020}+\dfrac{2020}{2021}+\dfrac{2021}{2018}>4\)
a) \(2\left(\dfrac{2}{3.5}+\dfrac{4}{5.9}+...+\dfrac{16}{n\left(n+16\right)}\right)=\dfrac{16}{25}\)
\(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{n}-\dfrac{1}{n+16}=\dfrac{8}{25}\)
\(\dfrac{1}{3}-\dfrac{1}{n+16}=\dfrac{8}{25}\)
\(\dfrac{n+13}{3\left(n+16\right)}=\dfrac{8}{25}\)
\(24n+384=25n+325\)
\(25n-24n=384-325\)
\(n=59\)
Đúng 0
Bình luận (0)
b) Sai đề nha
\(\left\{{}\begin{matrix}\dfrac{2018}{2019}< 1\\\dfrac{2019}{2020}< 1\\\dfrac{2020}{2021}< 1\\\dfrac{2021}{2022}< 1\end{matrix}\right.\)
\(\Rightarrow\dfrac{2018}{2019}+\dfrac{2019}{2020}+\dfrac{2020}{2021}+\dfrac{2021}{2022}< 4\)
Đúng 0
Bình luận (0)
chị ơi hình như chị nhầm rồi P/s cuối phải là 1/n.(n+6)thì phải
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
A = \(\dfrac{2022}{2021^{2^{ }}+1}\) + \(\dfrac{2022}{2021^{2^{ }}+2}\) + \(\dfrac{2022}{2021^2+3}\) + ... + \(\dfrac{2022}{2021^{2^{ }}+2021}\)
Chứng tỏ rằng A không phải số tự nhiên
1.Tìm các số tự nhiên a,b khác 0 sao cho : dfrac{a}{5}-dfrac{z}{b}dfrac{2}{15}.2.Tìm số tự nhiên n, để các biểu thức là số tự nhiên.a)Adfrac{4}{n-1}+dfrac{6}{n-1}-dfrac{3}{n-1}.b)Bdfrac{2n+9}{n+2}-dfrac{3n}{n+2}+dfrac{5n+1}{n+2}.giúp mình với mai mình nộp rồi
Đọc tiếp
1.Tìm các số tự nhiên a,b khác 0 sao cho :
\(\dfrac{a}{5}-\dfrac{z}{b}=\dfrac{2}{15}\).
2.Tìm số tự nhiên n, để các biểu thức là số tự nhiên.
a)A=\(\dfrac{4}{n-1}+\dfrac{6}{n-1}-\dfrac{3}{n-1}\).
b)B=\(\dfrac{2n+9}{n+2}-\dfrac{3n}{n+2}+\dfrac{5n+1}{n+2}\).
giúp mình với mai mình nộp rồi![]()
Bài 2:
a) Ta có: \(A=\dfrac{4}{n-1}+\dfrac{6}{n-1}-\dfrac{3}{n-1}\)
\(=\dfrac{4+6-3}{n-1}\)
\(=\dfrac{7}{n-1}\)
Để A là số tự nhiên thì \(7⋮n-1\)
\(\Leftrightarrow n-1\inƯ\left(7\right)\)
\(\Leftrightarrow n-1\in\left\{1;7\right\}\)
hay \(n\in\left\{2;8\right\}\)
Vậy: \(n\in\left\{2;8\right\}\)
Đúng 4
Bình luận (0)
ta có B=2n+9/n+2-3n+5n+1/n+2=4n+10/n+2 Để B là STN thì 4n+10⋮n+2 4n+8+2⋮n+2 4n+8⋮n+2 ⇒2⋮n+2 n+2∈Ư(2) Ư(2)={1;2} Vậy n=0
Đúng 0
Bình luận (0)
Cho a ϵ Z. Chứng tỏ \(A=\dfrac{a}{3}+\dfrac{a^2}{2}+\dfrac{a^3}{6}\) là số nguyên
Lời giải:
Ta có: \(A=\frac{a}{3}+\frac{a^2}{2}+\frac{a^3}{6}\)
\(\Leftrightarrow A=\frac{2a+3a^2+a^3}{6}\)
Xét tử số:
\(a^3+3a^2+2a=a(a^2+3a+2)\)
\(=a[a(a+2)+(a+2)]\)
\(=a(a+1)(a+2)\)
Vì $a,a+1$ là hai số nguyên liên tiếp nên
\(a(a+1)\vdots 2\Rightarrow a(a+1)(a+2)\vdots 2\)
\(\Leftrightarrow a^3+3a^2+2a\vdots 2\) (1)
Mặt khác \(a,a+1,a+2\) là ba số nguyên liên tiếp nên tích của chúng chia hết cho $3$
\(\Leftrightarrow a(a+1)(a+2)\vdots 3\)
\(\Leftrightarrow a^3+3a^2+2a\vdots 3\) (2)
Từ (1)(2) kết hợp với $(2,3)$ nguyên tố cùng nhau suy ra \(a^3+3a^2+2a\vdots 6\)
\(\Rightarrow A=\frac{a^3+3a^2+2a}{6}\in\mathbb{Z}\). Ta có đpcm.
Đúng 0
Bình luận (0)
Cho \(A=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2019}\)
Chứng minh A ko phải là số tự nhiên
A=1/2+1/3+..+1/2019 < 1>
A= 1+1/2+1/3+..+1/2019 < 1>
A=1+1/2+1/3+..+1/2019 <1>
A=1+1/2+1/3+..+1/2019 <2018>
Vì 2018/2019 <1>
nên A=1/2+1/3+..+1/2019<1>
=> A=1/2+1/3+..+1/2019 không phải là số tự nhiên.
Đúng 0
Bình luận (1)
Cho \(A=1+\dfrac{1}{4}+\dfrac{1}{9}+...+\dfrac{1}{n^2}\) với n là số tự nhiên. Chứng minh rằng \(A< \dfrac{7}{4}\).