Tìm các số nguyên tố x sao cho giá trị của biểu thức A là số chính
phương : A = x2 - 6x + 6 .
H24
Những câu hỏi liên quan
Tìm các số nguyên tố x sao cho giá trị của biểu thức A là số chính
phương : A = x2 - 6x + 6 .
Giả sử:
x² + x + 6 = k² ( k nguyên dương)
=> 4x² + 4x + 24 = 4k² => 4x² + 4x + 24 = 4k²
=> -(2x+1)² + 4k² = 23 => -(2x+1)² + 4k² = 23
=>(-2k+2x+1)(2k+2x+1) = -23 =>(-2k+2x+1)(2k+2x+1) = -23
Do x, k đều nguyên và k nguyên dương nên 2x + 2k + 1 > 2x +1-2k do đó chỉ xảy ra các trường hợp
TH1: -2k+2x+1 = -1 và 2k+2x+1 = 23
=> x = 5 và k = 6
TH2: -2k+2x+1 = -23 và 2k + 2x +1= 1
=> x = - 6 và k = 6 (loại vì k∈N)
Vậy x = 5
Đúng 1
Bình luận (2)
Tìm các số nguyên tố x sao cho giá trị của biểu thức A là số chính
phương : A = x 2 - 6x + 6 .
Tìm các số nguyên tố x sao cho giá trị của biểu thức A là số chính
phương : A = x2 - 6x + 6 .
Tìm các số nguyên tố x sao cho giá trị của biểu thức A là số chính
phương : A = x2 - 6x + 6 .
Tìm các số nguyên tố x sao cho giá trị của biểu thức A là số chính
phương : A = x2 - 6x + 6 .
A là số chính phương, suy ra
\(x^2-6x+6=k^2\) \(\left(k\inℕ\right)\)
\(\Leftrightarrow\left(x-3\right)^2-3=k^2\Leftrightarrow\left(x-3\right)^2-k^2=3\Leftrightarrow\left(x-3-k\right)\left(x-3+k\right)=3\)
Vì \(x;k\inℕ\Rightarrow x-3-k< x-3+k\)nên ta có các trường hợp sau
\(\hept{\begin{cases}x-3-k=1\\x-3+k=3\end{cases}}\Leftrightarrow\hept{\begin{cases}x=5\left(tm\right)\\k=1\end{cases}}\)
\(\hept{\begin{cases}x-3-k=-3\\x-3+k=-1\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\left(ktm\right)\\k=1\end{cases}}}\)
Vậy x=5 thì giá trị biểu thức A là số chính phương
Tìm các số nguyên tố x sao cho giá trị của biểu thức A là số chính
phương : A = x2 - 6x + 6 .
A = x2 - 6x + 6
= x2 - 2.x.3 + 32 - 3
=(x - 3)2 - 3
Ta có: \(\left(x-3\right)^2\ge0\forall x\)=> (x - 3)2 - 3 < 0 =>A < 0 =>A không là số chính phương(vì số chính phương luôn lớnhơnhoặc bằng0)
=> \(x\in\varnothing\)
Vậy không có số nguyên tố x nào thỏa mãn đề bài
À mình nhần rồi sr các bạn
Bài 1
Cho biểu thức : A= (2x-1)(4x2+2x+1)-7(x3+1)
a) rút gọn biểu thúc a
B) tính giá trị biểu thức a tại x=-1/2
C) tìm các giá trị nguyên của x để A có giá trị là số nguyên tố
a: \(A=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)
\(=\left(2x\right)^3-1^3-7x^3-7\)
\(=8x^3-1-7x^3-7=x^3-8\)
b: Thay x=-1/2 vào A, ta được:
\(A=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)
Đúng 0
Bình luận (1)
Bài 1
Cho biểu thức : A= (2x-1)(4x2+2x+1)-7(x3+1)
a) rút gọn biểu thúc a
B) tính giá trị biểu thức a tại x=-1/2
C) tìm các giá trị nguyên của x để A có giá trị là số nguyên tố
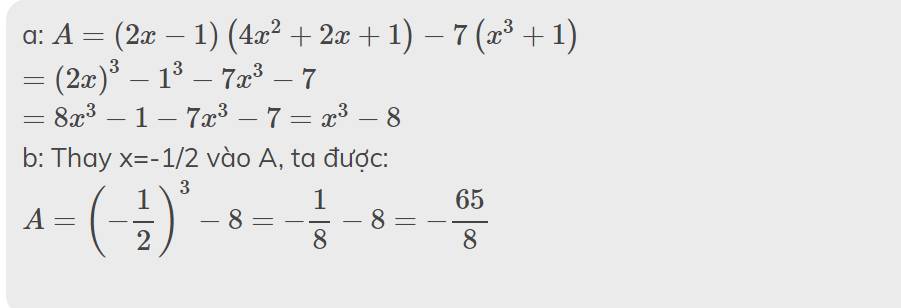
c: \(A=x^3-8=\left(x-2\right)\left(x^2+2x+4\right)\)
Để A là số nguyên tố thì x-2=1
=>x=3
Đúng 0
Bình luận (0)
Cho biểu thức A (x – 2)(x+4) Tìm số tự nhiên x để A có giá trị là số nguyên tố Tìm số nguyên x để biểu thức A có giá trị là số âmMình cần gấp lắm. Giúp mình với.
Đọc tiếp
Cho biểu thức A= (x – 2)(x+4)
Tìm số tự nhiên x để A có giá trị là số nguyên tố
Tìm số nguyên x để biểu thức A có giá trị là số âm
Mình cần gấp lắm. Giúp mình với.
Lời giải:
a. Để A là số nguyên tố thì 1 trong 2 thừa số $x-2, x+4$ có giá trị bằng 1 và số còn lại là số nguyên tố.
Mà $x-2< x+4$ nên $x-2=1$
$\Rightarrow x=3$
Thay vào $A$ thì $A=7$ là snt (thỏa mãn)
b. Để $A<0\Leftrightarrow (x-2)(x+4)<0$
Điều này xảy ra khi $x-2,x+4$ trái dấu. Mà $x-2< x+4$ nên:
$x-2<0< x+4$
$\Rightarrow -4< x< 2$
$x$ nguyên nên $x=-3,-2,-1,0,1$
Đúng 5
Bình luận (0)



