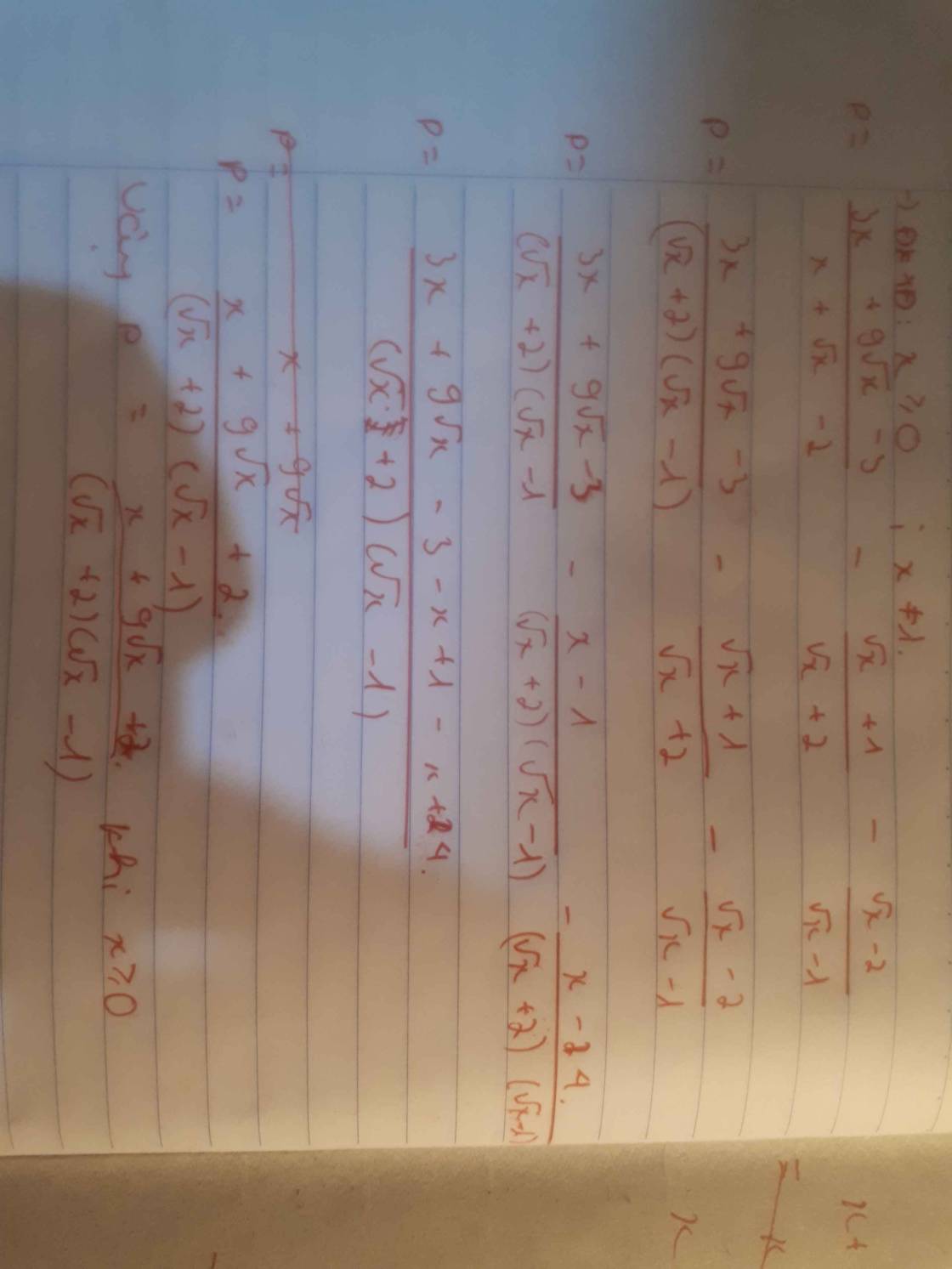Rút gọn biểu thức M=\(\sqrt[3]{3x-1+x\sqrt{8x-3}}\)+\(\sqrt[3]{3x-1-x\sqrt{8x-3}}\)
H24
Những câu hỏi liên quan
Rút gọn biểu thức sau:
a)M=\(3x-\sqrt[3]{27^3+27x^2+9x+1}\)
b)N=\(\sqrt[3]{8x^3+12x^2+6x+1}-\sqrt[3]{x^3}\)
a: Sửa đề: \(M=3x-\sqrt[3]{27x^3+27x^2+9x+1}\)
\(=3x-\sqrt[3]{\left(3x\right)^3+3\cdot\left(3x\right)^2\cdot1+3\cdot3x\cdot1^2+1^3}\)
\(=3x-\sqrt[3]{\left(3x+1\right)^3}\)
\(=3x-3x-1=-1\)
b: \(N=\sqrt[3]{8x^3+12x^2+6x+1}-\sqrt[3]{x^3}\)
\(=\sqrt[3]{\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot1+3\cdot2x\cdot1^2+1^3}-x\)
\(=\sqrt[3]{\left(2x+1\right)^3}-x\)
=2x+1-x
=x+1
Đúng 0
Bình luận (0)
rút gọn các biểu thức sau với x ≥ 0
a) \(2\sqrt{3x}-4\sqrt{3x}+27-3\sqrt{3x}\)
b) \(3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+28\)
\(a,=27-5\sqrt{3x}\\ b,=3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}+28=14\sqrt{2x}+28\)
Đúng 2
Bình luận (0)
RÚT GỌN A=\(\frac{\sqrt{x}+3}{6+5\sqrt{x}+6}:\left(\frac{8x}{4x\sqrt{x-8x}}-\frac{3\sqrt{x}}{3x-12}-\frac{1}{\sqrt{x}+2}\right)\)
Để \(\sqrt{x}\) xác định
\(\Leftrightarrow x\ge0\)
\(\Leftrightarrow-7x\le0\)
\(\Rightarrow\sqrt{-7x}\)không tồn tại
\(\Leftrightarrow\frac{8x}{4x\sqrt{x-8x}}\)không tồn tại
=> A không tồn tại
Rút gọn các biểu thức sau:
a) \(A=3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+30\), \(x\ge0\)
b) \(B=4\sqrt{\dfrac{25x}{4}}-\dfrac{8}{3}\sqrt{\dfrac{9x}{4}}-\dfrac{4}{3x}\sqrt{\dfrac{9x^3}{64}}\), \(x>0\)
c) \(C=\dfrac{y}{2}+\dfrac{3}{4}\sqrt{1+9y^2-6y}-\dfrac{3}{2}\), \(y\le\dfrac{1}{3}\)
a) Ta có: \(A=3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+30\)
\(=3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}+30\)
\(=14\sqrt{2x}+30\)
b) Ta có: \(B=4\sqrt{\dfrac{25x}{4}}-\dfrac{8}{3}\sqrt{\dfrac{9x}{4}}-\dfrac{4}{3x}\cdot\sqrt{\dfrac{9x^3}{64}}\)
\(=4\cdot\dfrac{5\sqrt{x}}{2}-\dfrac{8}{3}\cdot\dfrac{3\sqrt{x}}{2}-\dfrac{4}{3x}\cdot\dfrac{3x\sqrt{x}}{8}\)
\(=10\sqrt{x}-4\sqrt{x}-\dfrac{1}{2}\sqrt{x}\)
\(=\dfrac{11}{2}\sqrt{x}\)
c) Ta có: \(\dfrac{y}{2}+\dfrac{3}{4}\sqrt{9y^2-6y+1}-\dfrac{3}{2}\)
\(=\dfrac{1}{2}y+\dfrac{3}{4}\left(1-3y\right)-\dfrac{3}{2}\)
\(=\dfrac{1}{2}y+\dfrac{3}{4}-\dfrac{9}{4}y-\dfrac{3}{2}\)
\(=-\dfrac{7}{4}y-\dfrac{3}{4}\)
Đúng 2
Bình luận (0)
cho biểu thức \(P=\dfrac{x^2+3x}{x^2-8x+16}:\left(\dfrac{x+4}{x}+\dfrac{1}{x-4}+\dfrac{19-x^2}{x^2-4x}\right)\)
a) rút gọn P
b) tính giá trị của P tại \(x=\sqrt{4+2\sqrt{3}}-\sqrt{4-2\sqrt{3}}\)
a) \(P=\dfrac{x^2+3x}{x^2-8x+16}:\left(\dfrac{x+4}{x}+\dfrac{1}{x-4}+\dfrac{19-x^2}{x^2-4x}\right)\left(x\ne0,x\ne4\right)\)
\(=\dfrac{x^2+3x}{\left(x-4\right)^2}:\left(\dfrac{x+4}{x}+\dfrac{1}{x-4}+\dfrac{19-x^2}{x\left(x-4\right)}\right)\)
\(=\dfrac{x^2+3x}{\left(x-4\right)^2}:\dfrac{\left(x+4\right)\left(x-4\right)+x+19-x^2}{x\left(x-4\right)}\)
\(=\dfrac{x^2+3x}{\left(x-4\right)^2}:\dfrac{x+3}{x\left(x-4\right)}=\dfrac{x\left(x+3\right)}{\left(x-4\right)^2}.\dfrac{x\left(x-4\right)}{x+3}=\dfrac{x^2}{x-4}\)
b) \(x=\sqrt{4+2\sqrt{3}}-\sqrt{4-2\sqrt{3}}=\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=\sqrt{3}+1-\sqrt{3}+1=2\)
\(\Rightarrow P=\dfrac{2^2}{2-4}=-2\)
Đúng 1
Bình luận (0)
a)\(ĐKXĐ:\left\{{}\begin{matrix}x\left(x-4\right)\ne0\\\dfrac{x+4}{x}+\dfrac{1}{x-4}+\dfrac{19-x^2}{x^2-4x}\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne4\\x\ne0\\x\ne-3\end{matrix}\right.\)
\(P=\dfrac{x\left(x+3\right)}{\left(x-4\right)}:\left(\dfrac{x^2-16+x+19-x^2}{x\left(x-4\right)}\right)=\dfrac{x\left(x+3\right)}{\left(x-4\right)^2}.\left(\dfrac{x\left(x-4\right)}{x+3}\right)=\dfrac{x^2}{x-4}\)
b)\(x=\sqrt{4+2\sqrt{3}}-\sqrt{4-2\sqrt{3}}=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3+1}-\left(\sqrt{3}-1\right)=2\)
thay x=2 vào P ta có \(P=\dfrac{2^2}{2-4}=-2\)
Đúng 0
Bình luận (0)
Rút gọn các biểu thức sau với \(x\ge0:\)
a. \(2\sqrt{3x}-4\sqrt{3x}+27-3\sqrt{3x};\)
b. \(3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+28.\)
a)
Lưu ý. Các căn số bậc hai là những số thực. Do đó khó làm tính với căn số bậc hai, ta có thể vận dụng mọi quy tắc và mọi tính chất của các phép toàn trên số thực.
b) Dùng phép đưa thừa số ra ngoài dấu căn để có những căn thức giống nhau là .
ĐS:
Đúng 0
Bình luận (0)
a)
Lưu ý. Các căn số bậc hai là những số thực. Do đó khó làm tính với căn số bậc hai, ta có thể vận dụng mọi quy tắc và mọi tính chất của các phép toàn trên số thực.
b) Dùng phép đưa thừa số ra ngoài dấu căn để có những căn thức giống nhau là .
ĐS:
Đúng 0
Bình luận (0)
dựng hình thang ABCD (AB//CD),biết AB=AD=2cm,AC=AD 4cm
Đúng 0
Bình luận (0)
Rút gọn các biểu thức sau với x>= 0:
a)\(2\sqrt{3x}-4\sqrt{3x}+27-3\sqrt{3x}\)
b)\(3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+28\)
giải phương trình sau:
a) \(4x^2+\left(8x-4\right).\sqrt{x}-1=3x+2\sqrt{2x^2+5x-3}\)
b) \(8x^3-36x^2+\left(1-3x\right)\sqrt{3x-2}-3\sqrt{3x-2}+63x-32=0\)
c) \(2\sqrt[3]{3x-2}-3\sqrt{6-5x}+16=0\)
d) \(\sqrt[3]{x+6}-2\sqrt{x-1}=4-x^2\)
Rút gọn biểu thức P= \(\dfrac{3x+9\sqrt{x}-3}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}-\dfrac{\sqrt{x}-2}{\sqrt{x}-1}\)
Tìm x để P= 3.
Sửa đề: 3x+căn 9x-3
\(P=\dfrac{3x+3\sqrt{x}-3-x+1-x+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+3\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
P=3
=>căn x+1=3căn x-3
=>-2căn x=-4
=>x=4
Đúng 0
Bình luận (1)