Cho hình bình hành ABCDcó tọa độ ba đỉnh là: A(2 ; 2) , B(11 ; 2) ; D(-1 ; -3). Tọa độ đỉnh C là ?
NL
Những câu hỏi liên quan
Cho hình bình hành ABCD có tọa độ ba đỉnh là : A(3 ; -2) , B(14 ; -2) , D(0 ; -8) . Tính tọa độ C (... ; ...) ?
Cho ba điểm A (1;-2), B (2;3), C (-1;-2).
a) Tìm tọa độ điểm D đối xứng của A qua C.
b) Tìm tọa độ điểm E là đỉnh thứ tư của hình bình hành có 3 đỉnh là A, B, C.
c) Tìm tọa độ trọng tâm G của tam giác ABC
\(a,\Rightarrow C,A,D\) \(thẳng\) \(hàng\Rightarrow\overrightarrow{CA}+\overrightarrow{CD}=\overrightarrow{0}\Leftrightarrow\overrightarrow{CA}=\overrightarrow{DC}\)
\(D\left(x;y\right)\Rightarrow\overrightarrow{CA}=\overrightarrow{DC}\Leftrightarrow\left\{{}\begin{matrix}-1-x=2\\-2-y=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-2\end{matrix}\right.\)\(\Rightarrow D\left(-3;-2\right)\)
\(b,E\left(xo;yo\right)\Rightarrow\overrightarrow{AE}=\overrightarrow{BC}\)\(\Leftrightarrow\left\{{}\begin{matrix}xo-1=-3\\yo+2=-5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}xo=-2\\yo=-7\end{matrix}\right.\)\(\Rightarrow E\left(-2;-7\right)\)
\(c,\Rightarrow G\left(xG;yG\right)\Rightarrow\left\{{}\begin{matrix}xG=\dfrac{1+2-1}{3}=\dfrac{2}{3}\\yG=\dfrac{-2+3-2}{3}=-\dfrac{1}{3}\end{matrix}\right.\)\(\Rightarrow G\left(\dfrac{2}{3};-\dfrac{1}{3}\right)\)
Đúng 1
Bình luận (0)
1.Trong mặt phẳng tọa độ Oxy cho hình bình hành ABCD với A (- 6;1); B (2;2) C (1;5) tọa độ đỉnh D là:
A. (5;2)
B. (-7;4)
C. (5;4)
D. (7;-4)
2.Trong mặt phẳng tọa độ Oxy cho tam giác ABC với A (- 1;3); B (2;1) C (5;5) tọa độ đỉnh D là của hình bình hành ABCD:
A. (0;4)
B. (8;1)
C. (8;3)
D. (-8;3)
Hướng dẫn em cách làm với ạ. Em cảm ơn nhiều.
1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)
Đúng 1
Bình luận (1)
Ba đỉnh của một hình bình hành có tọa độ là (1;1;1), (2;3;4), (7;7;5). Diện tích của hình bình hành đó bằng A. 2
83
B.
83
C. 83 D.
83
2
Đọc tiếp
Ba đỉnh của một hình bình hành có tọa độ là (1;1;1), (2;3;4), (7;7;5). Diện tích của hình bình hành đó bằng
A. 2 83
B. 83
C. 83
D. 83 2
Đáp án A
Gọi 3 đỉnh theo thứ tự là A, B,C
![]()
![]()
Đúng 0
Bình luận (0)
Ba đỉnh của một hình bình hành có tọa độ là
1
;
1
;
1
,
2
;
3
;
4
,
7
;
7
;
5
.
Diện tích của...
Đọc tiếp
Ba đỉnh của một hình bình hành có tọa độ là 1 ; 1 ; 1 , 2 ; 3 ; 4 , 7 ; 7 ; 5 . Diện tích của hình bình hành đó bằng
A. 2 83
B. 83
C. 83
D. 83 2
Đáp án A
Gọi 3 đỉnh theo thứ tự là A, B,C
A B → = 1 ; 2 ; 3 , A C → = 6 ; 6 ; 4 S h b h = 2 S A B C = A B . A B . sin A = 2 83
Đúng 0
Bình luận (0)
cho hình bình hành có tọa độ một đỉnh là (4,-1) . Biết phương trình các đường thẳng chứa 2 cạnh là x-3y=0 và 2x+5y+6=0 . Tìm tọa độ 3 đỉnh conf lại của hình bình hành đó .
cho ba điểm A(-1,6); B(-4,4);C(1;1).tìm tọa độ đỉnh D của hình bình hành ABCD
Độ dài đoạn thẳng AB là: \(AB=\sqrt{\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2}=\sqrt{\left[-1-\left(-4\right)\right]^2+\left(6-4\right)^2}=\sqrt{9+4}=\sqrt{13}\)
Mà CD = AB (vì tứ giác ABCD là hình bình hành) \(\Rightarrow CD=\sqrt{13}\)
Tương tự, ta cũng tính được độ dài đoạn AD là \(\sqrt{34}\)
Như vậy, ta có \(\hept{\begin{cases}CD=\sqrt{13}=\sqrt{\left(x_C-x_D\right)^2+\left(y_C-y_D\right)^2}\\AD=\sqrt{34}=\sqrt{\left(x_A-x_D\right)^2+\left(y_A-y_D\right)^2}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\sqrt{\left(1-x_D\right)^2+\left(1-y_D\right)^2}=\sqrt{13}\\\sqrt{\left(-1-x_D\right)^2+\left(6-y_D\right)^2}=\sqrt{34}\end{cases}}\)
Tới đây bạn tự giải nhé.
Cho hình bình hành ABCD với
A
−
2
;
3
;
1
,
B
3
;
0
;
−
1
,
C
6
;
5
;
0
.
Tọa độ đỉnh D là A....
Đọc tiếp
Cho hình bình hành ABCD với A − 2 ; 3 ; 1 , B 3 ; 0 ; − 1 , C 6 ; 5 ; 0 . Tọa độ đỉnh D là
A. D(1;8;-2)
B. D(11;2;2)
C. D(1;8;2)
D. D(11;2;-2)
Chọn C.
Phương pháp:
ABCD là hình bình hành khi và chỉ khi A, B, C, D phân biệt, không thẳng hàng và
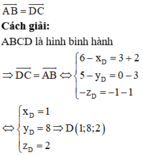
Đúng 0
Bình luận (0)
A(2 ; 4)B(15 ; 4)D(-1 ; -2)C(? ; ?)
Cho hình bình hành ABCDABCD có tọa độ ba đỉnh là: A(2 ; 4)A(2;4) , B(15 ; 4)B(15;4) ; D(-1 ; -2)D(−1;−2). Tọa độ đỉnh C là (( ; )).




