Giúp mình với ạ, mình cần gấp!!
Giải tam giác nhọn ABC biết góc B = 60o, AB = 3,0 và BC = 4,5.
Giúp mình với ạ, mình cầ rất gấp!!!
Giải tam giác ABC vuông tại A, biết
a) BC = 4,5 và góc C = 35o;
b) AB = 3,1 và bóc B = 65o.
a: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=55^0\)
Xét ΔABC vuông tại A có
\(AC=BC\cdot\sin55^0\)
\(\Leftrightarrow AC\simeq3.69\left(cm\right)\)
\(\Leftrightarrow AB\simeq2.58\left(cm\right)\)
Giúp mình với ạ, mình cần gấp!!!
Bài 1. Giải tam giác ABC vuông tại A, biết
a) AB = 2,7 và AC = 4,5
b) AC = 4,0 và BC = 4,8
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay \(BC=\dfrac{9\sqrt{34}}{10}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{5\sqrt{34}}{34}\)
\(\Leftrightarrow\widehat{B}\simeq59^0\)
\(\Leftrightarrow\widehat{C}=21^0\)
cho tam giác nhọn ABC có AB=15cm, AC=13cm, đường cao AH=12cm.Gọi M,N lần lượt là hình chiếu vuông góc của H xuống AB và AC
a/ tam giác AHN đồng dạng với tam giác ACH
b/ tính BC
c/ tam giác AMN đồng dạng với tam giác ACB
d/ tính MN
giúp mình với , mình cần gấp ạ
Bài làm
a) Vì AH vuông góc với BC
=> Tam giác AHC vuông ở H.
=> \(\widehat{HAC}+\widehat{C}=90^0\) (1)
Vì HN vuông góc với AC
=> Tam giác HNC vuông ở N
=> \(\widehat{NHC}+\widehat{C}=90^0\) (2)
Từ (1) và (2) => \(\widehat{HAC}=\widehat{NHC}\)
Xét tam giác AHN và tam giác ACH có:
\(\widehat{ANH}=\widehat{HNC}\left(=90^0\right)\)
\(\widehat{HAC}=\widehat{NHC}\)
=> Tam giác AHN ~ tam giác ACH ( g - g )
b) Xét tam giác AHB vuông ở H,
Theo định lí Thales có:
\(AB^2=AH^2+HB^2\)
Hay \(15^2=12^2+HB^2\)
\(\Rightarrow225=144+HB^2\)
\(\Rightarrow HB^2=81\)
\(\Rightarrow HB=9\left(cm\right)\)
Xét tam giác AHC vuông ở H có:
\(AC^2=AH^2+HC^2\)
hay \(13^2=12^2+HC^2\)
\(\Rightarrow169=144+HC^2\)
\(\Rightarrow HC^2=25\left(cm\right)\)
\(\Rightarrow HC=5\left(cm\right)\)
Ta có: HB + HC = BC
hay 9 + 5 = BC
=> BC = 14 ( cm )
Cho tam giác nhọn ABC. Vẽ AH vuông góc BC. Biết HB<HC. CMR: AB<AC.
Giúp mình với ạ. mình sẽ tim cho ạ
`@` `\text {Ans}`
`\downarrow`
Ta có: AH là đường vuông góc của `\Delta ABC`
`=>` AB, AC là đường xiên
`=> HB, HC` lần lượt là hình chiếu của AB, AC
`@` Theo định lý quan hệ giữa đường xiên và hình chiếu (Đường xiên có hình chiếu lớn hơn thì lớn hơn. Đường xiên có hình chiếu nhỏ hơn thì nhỏ hơn. Các đường xiên bằng nhau thì hình chiếu cũng bằng nhau.)
`=>` AB < AC.
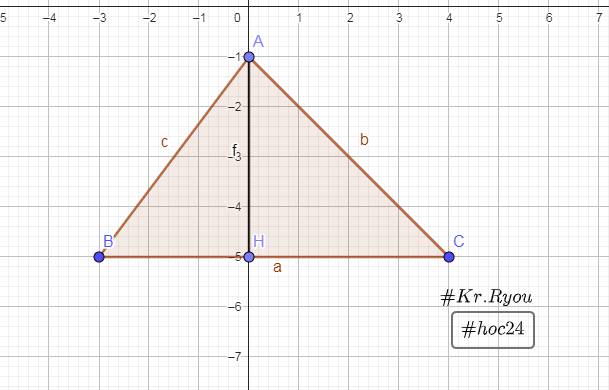
Vẽ tam giác ABC biết:
a)AB=3 cm;BC=5 cm;AC=4 cm.Đo và cho biết số đo của góc A
b)AB=6 cm;BC= 7 cm;AC= 8 cm
giúp mình với mình đang cần gấp ạ ai nhanh và đúng nhất mình sẽ tick
bạn dùng com-pa mà vẽ
kẻ đoạn bc= 5cho khẩu lộ com-pa là 3 vẽ đường tròn tâm bcho khẩu lộ com-pa là 4 vẽ đường tròn tâm chai đường tron cắt nhau ở đâu thì đó là điểm anối các điểm lại với nhau rồi tự đo góc nhécâu 2 cũng làm tương tựxin lỗi phiền bạn vẽ hộ ra và đo góc hộ mình đc ko mình k biết đo góc A còn vẽ mình biết r
tam giác ABC có AB=7cm;AC=5cm;BC=6cm.So sánh các góc của tam giác ABC giúp với ạ mình cần gấp:((((
Ta có AB > BC > AC -> ^C > ^A > ^B
tam giác ABC có AB=7cm;AC=5cm;BC=6cm
\(=>AB>BC>AC\)
\(=>\widehat{C}>\widehat{A}>\widehat{B}\)
Cho tam giác nhọn ABC, đường cao AD (D thuộc BC). Gọi M, N lần lượt là hình chiếu vuông góc của D trên AB, AC. Chứng minh rằng:
1. Hai tam giác AMN và ACB đồng dạng.
2. MN=AD.sin BAC
Giúp mình câu 2 với ạ, mình đang cần gấp. Mình cảm ơn ạ
Trong tam giác AMN, ta có:
MN = AN.sin(∠MAN) (định lí sin)
Vì MN là hình chiếu vuông góc của D lên AB và AC, nên AN = AD.cos(∠BAC) và AM = AD.cos(∠CAB). Thay vào công thức trên, ta có:
MN = AD.cos(∠CAB).sin(∠BAC)
Do đó, để chứng minh MN = AD.sin(BAC), ta cần chứng minh rằng:
cos(∠CAB).sin(∠BAC) = sin(∠BAC)
Áp dụng định lí sin, ta có:
cos(∠CAB).sin(∠BAC) = sin(∠BAC).cos(∠CAB)
Vì cos(∠CAB) = cos(90° - ∠BAC) = sin(∠BAC), nên:
sin(∠BAC).cos(∠CAB) = sin(∠BAC).sin(∠BAC) = sin^2(∠BAC)
Vậy, MN = AD.sin(BAC).
Như vậy, đã chứng minh hai điều kiện trên.
Cho tamtam g nhọn ABC có AB > AC, kẻ AH vuông góc với BC (H thuộc BC) AC là tia phân giác của góc HAC vuông góc với AC Chứng minh rằng
A) tam giác HAC =tam giác DAE
B) EC>HE.
C) Số sánh BAH và HAC
Giúp mình với mình đang cần gấp 🙂🙂
Tam giác ABC (A=90 độ) : AB<AC, phân giác BD kẻ đường thẳng qua D vuông góc với BC tại E
a) Chứng minh tam giác ABC cân
b) Chứng minh AD < DC
c) CF vuông góc BD tại F. Chứng minh AB, DE, CF đồng quy
giúp mình với mình cần gấp ạ