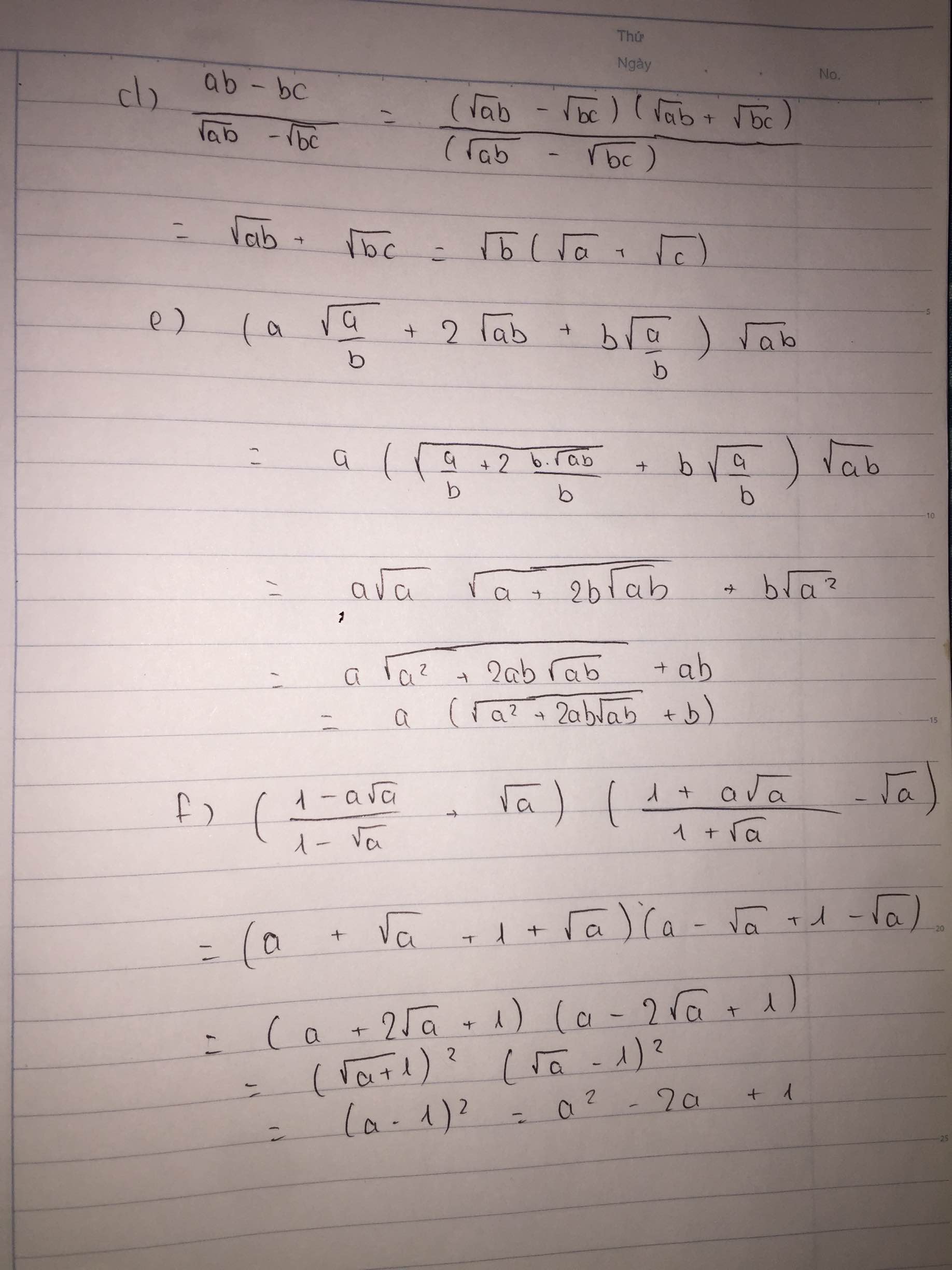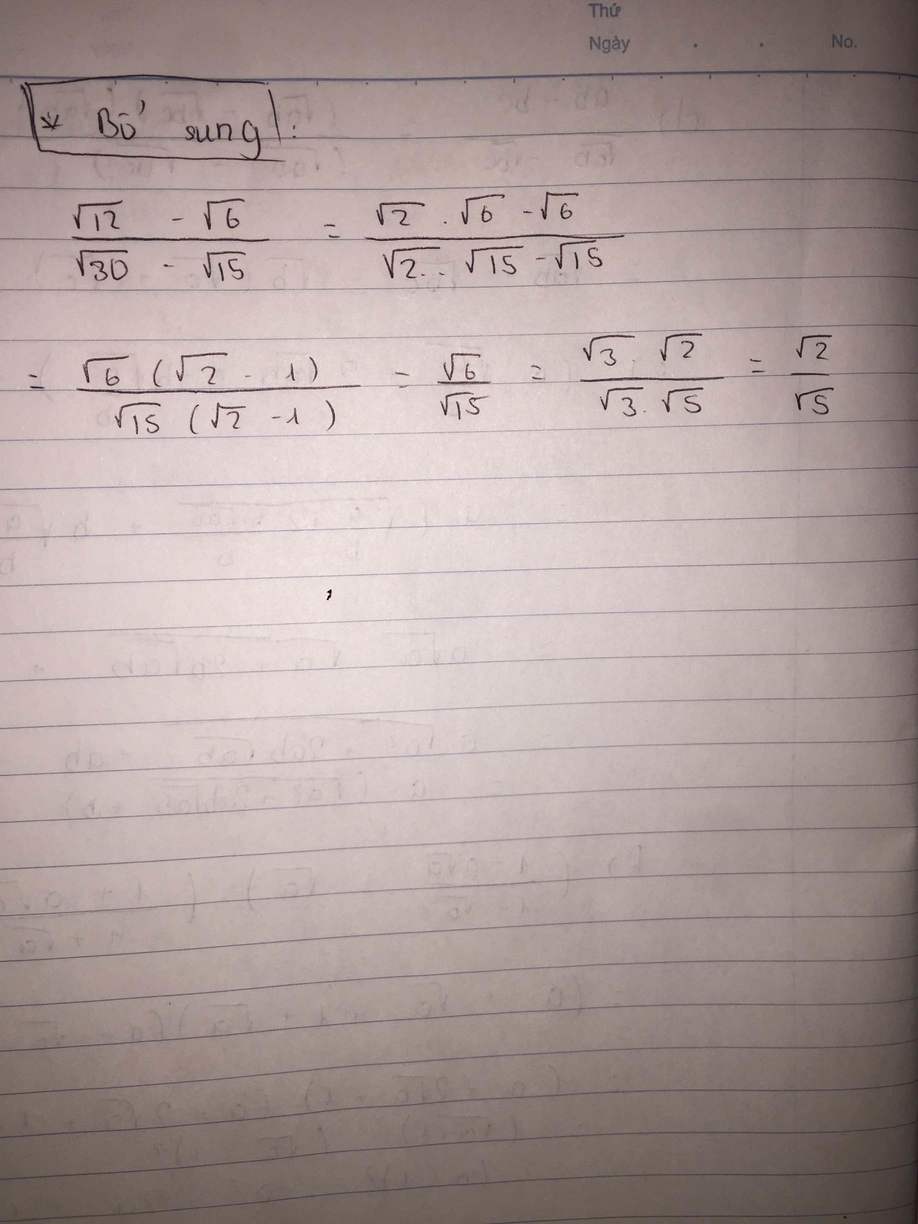Đây là bài tập hay đang kiểm tra đây em? :)

ĐKXĐ: \(x\ge0\)

Với \(x=0\) ko phải nghiệm

Với \(x>0\) chia 2 vế cho \(x\) ta được:

\(\dfrac{2x^2+1}{x}-2m=3\sqrt{\dfrac{2x^2+1}{x}}-4\)

Đặt \(\sqrt{\dfrac{2x^2+1}{x}}=t\ge\sqrt{2\sqrt{2}}=\sqrt[4]{8}\)

\(\Rightarrow2x^2-tx+1=0\) (1)

\(\Delta=t^2-8\Rightarrow\) ứng với mỗi giá trị  t thì:

- Nếu \(t>2\sqrt{2}\Rightarrow\left(1\right)\) có 2 nghiệm pb

- Nếu \(t=2\sqrt{2}\Rightarrow\left(1\right)\) có 1 nghiệm kép

- Nếu \(t< 2\sqrt{2}\) thì (1) vô nghiệm

Pt đã cho trở thành \(t^2-3t+4=2m\) (2)

Xét hàm \(f\left(t\right)=t^2-3t+4\) với \(t\ge\sqrt[4]{8}\)

\(a=1>0;-\dfrac{b}{2a}=\dfrac{3}{2}< \sqrt[4]{8}\Rightarrow f\left(t\right)\) đồng biến khi \(t\ge\sqrt[4]{8}\)

\(\Rightarrow y=2m\) cắt \(y=f\left(t\right)\) tại tối đa 1 điểm hay (2) có tối đa 1 nghiệm t

\(\Rightarrow\) Pt đã cho có 2 nghiệm pb khi và chỉ khi (2) có nghiệm thỏa mãn \(t>2\sqrt{2}\)

\(\Rightarrow2m>f\left(2\sqrt{2}\right)=12-6\sqrt{2}\Rightarrow m>6-3\sqrt{2}\)

Có 19 giá trị nguyên của m 

2b.

\(Q=\dfrac{cosx}{sinx}+\dfrac{sinx}{1+cosx}=\dfrac{cosx\left(1+cosx\right)+sin^2x}{sinx\left(1+cosx\right)}=\dfrac{cosx+cos^2x+sin^2x}{sinx\left(1+cosx\right)}=\dfrac{cosx+1}{sinx\left(1+cosx\right)}=\dfrac{1}{sinx}\)

4b.

\(\Delta\) có 1 vtpt là (3;-4)

Gọi d là đường thẳng qua M và vuông góc \(\Delta\Rightarrow d\) nhận (4;3) là 1 vtpt

Phương trình d:

\(4\left(x-4\right)+3\left(y+2\right)=0\Leftrightarrow4x+3y-10=0\)

H là giao điểm d và \(\Delta\) nên tọa độ thỏa mãn:

\(\left\{{}\begin{matrix}3x-4y+5=0\\4x+3y-10=0\end{matrix}\right.\) \(\Rightarrow H\left(1;2\right)\)

a: góc AED+góc AFD=180 độ

=>AEDF nội tiếp

=>góc AEF=góc ADF=góc C

=>góc FEB+góc FCB=180 độ

=>FEBC nội tiếp

b: Xét ΔGBE và ΔGFC có

góc GBE=góc GFC

góc G chung

=>ΔGBE đồng dạng với ΔGFC

=>GB/GF=GE/GC

=>GB*GC=GF*GE

tk:

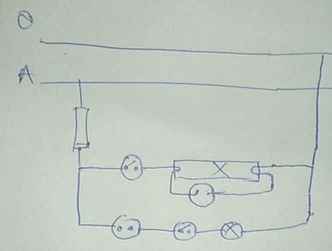
vẽ lại mạch ta có RAM//RMN//RNB

đặt theo thứ tự 3 R là a,b,c

ta có a+b+c=1 (1)

điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0

áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\)  \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)

\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)

dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)

từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)

vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )

em ơi chụp cả cái mạch điện a xem nào sao chụp nó bị mất r

Do vai trò của 3 biến là như nhau, không mất tính tổng quát giả sử \(x>y>z\)

Ta có: \(x-z=\left(x-y\right)+\left(y-z\right)\)

Đặt \(\left\{{}\begin{matrix}x-y=a>0\\y-z=b>0\end{matrix}\right.\)  

Do \(x;z\in\left[0;2\right]\Rightarrow x-z\le2\) hay \(a+b\le2\)

Ta có:

\(P=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{4}{a+b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\)

\(P\ge\dfrac{9}{\left(a+b\right)^2}\ge\dfrac{9}{2^2}=\dfrac{9}{4}\)

Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a=b\\a+b=2\\\end{matrix}\right.\) \(\Rightarrow a=b=1\) hay \(\left(x;y;z\right)=\left(0;1;2\right)\) và các hoán vị

\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)

\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)

\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)

\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)

\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)

\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)

\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)

\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)

\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)

\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)

\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)

\(=\left(a-1\right)^2=a^2-2a+1\)

a: Xét ΔABM và ΔACM có

AB=AC

AM chung

BM=CM

Do đó:ΔABM=ΔACM

b: ta có: ΔABC cân tại A

mà AM là đường trung tuyến

nên AM là đường cao

c: BC=6cm

nên BM=3cm

=>AM=4cm

d: Xét ΔABC cân tại A có AM là đường cao

nên AM là phân giác của góc BAC

Xét ΔABC có

AM là đường phân giác

BI là đường phân giác

AM cắt BI tại I

Do đó: CI là tia phân giác của góc ACB

a: Xét ΔABM và ΔACM có

AB=AC

AM chung

BM=CM

Do đó:ΔABM=ΔACM

b: ta có: ΔABC cân tại A

mà AM là đường trung tuyến

nên AM là đường cao

c: BC=6cm

nên BM=3cm

=>AM=4cm

d: Xét ΔABC cân tại A có AM là đường cao

nên AM là phân giác của góc BAC

Xét ΔABC có

AM là đường phân giác

BI là đường phân giác

AM cắt BI tại I

Do đó: CI là tia phân giác của góc ACB

a) Xét 2 tam giác ABM và tam giác ACM:

Có: góc ABM= góc ACM (tam giác ABC cân) ; BM=MC và AM chung

 ==>tam giác ABM=tam giác ACM
b)Trong một tam giác cân, đường trung trực ứng với cạnh đáy cũng đồng thời là đường phân giác
Xét tam giác ABC cân và có AM là trung trực (M là tđ BC)

==> AM là đường cao Tam giác ABC

==> AM vuông góc BC

c)Có M là trung điểm BC

==> BM=MC=1/2 BC

Mà BC =6cm

==> BM=3cm

Áp dụng định lý Pitago trong tam giác ABM : Góc AMB=90 độ

==> AM^2+BM^2=AB^2
       AM^2+3^2=5^2
==> AM =4cm

d) Xét tam giác IMB và tam giác IMC : góc IMC=Góc IMB(=90 độ)

IM chung;BM=MC(gt)

==> Tam Giác IMB=Tam giác IMC (c.g.c)

==> góc IBM=góc ICM                        
Mà góc ABM=Góc ACM (gt)

==> góc ABI+IBM=góc ACI+ICM

mà góc IBM=góc ICM  

==> góc ABI= góc ACI

từ đó ==> góc ACM=ICM

==> CI là phân giác góc C

Bài của chị chỉ dùng tham khảo thôi nha ,có chỗ nào không hiểu thì nhắn lại nha!

Chúc em học tốt *\(^o^)/*