giải phương trình:
\(\sin3x+3\sin2x-\sin x=\cos2x+3\cos x\)
giải các phương trình : a) \(\sin x+\sin2x+\sin3x=\cos x+\cos2x+\cos3x\) ; b) \(\sin x=\sqrt{2}\sin5x-\cos x\) ; c) \(\frac{1}{\sin2x}+\frac{1}{\cos2x}=\frac{2}{\sin4x}\) ; d)
\(\sin x+\cos x=\frac{\cos2x}{1-\sin2x}\)
giải các phương trình : a) \(\sin x+\sin2x+\sin3x=\cos x+\cos2x+\cos3x\) ; b) \(\sin x=\sqrt{2}\sin5x-\cos x\) ; c) \(\frac{1}{\sin2x}+\frac{1}{\cos2x}=\frac{2}{\sin4x}\) ; d)
\(\sin x+\cos x=\frac{\cos2x}{1-\sin2x}\)
giải phương trình: \(\sin2x+3\cos2x+8\sin x+14\cos x+11=0\)
Giải các phương trình sau:
1. tan2x+3= (1+√2 sin x)(tan x+ √2 cos x)
2. (1- cos x. cos2x )/ sin2x - 1/ cos x= 4 sin2x - sin x-1
3. sin3x + 2 cos3x+ cos2x - 2sin2x - 2sinx-1=0
1,Giải phương trình:
a,\(cos^3x+sin^3x=cos2x\)
b,\(cos^3x+sin^3x=2sin2x+sinx+cosx\)
c,\(2cos^3x=sin3x\)
d,\(cos^2x-\sqrt{3}sin2x=1+sin^2x\)
e,\(cos^3x+sin^3x=2\left(cos^5x+sin^5x\right)\)
a, (sinx + cosx)(1 - sinx . cosx) = (cosx - sinx)(cosx + sinx)
⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\cosx-sinx=1-sinx.cosx\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\cosx+sinx.cosx-1-sinx=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\\left(cosx-1\right)\left(sinx+1\right)=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}sin\left(x+\dfrac{\pi}{4}\right)=0\\cosx=1\\sinx=-1\end{matrix}\right.\)
b, (sinx + cosx)(1 - sinx . cosx) = 2sin2x + sinx + cosx
⇔ (sinx + cosx)(1 - sinx.cosx - 1) = 2sin2x
⇔ (sinx + cosx).(- sinx . cosx) = 2sin2x
⇔ 4sin2x + (sinx + cosx) . sin2x = 0
⇔ \(\left[{}\begin{matrix}sin2x=0\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+4=0\end{matrix}\right.\)
⇔ sin2x = 0
c, 2cos3x = sin3x
⇔ 2cos3x = 3sinx - 4sin3x
⇔ 4sin3x + 2cos3x - 3sinx(sin2x + cos2x) = 0
⇔ sin3x + 2cos3x - 3sinx.cos2x = 0
Xét cosx = 0 : thay vào phương trình ta được sinx = 0. Không có cung x nào có cả cos và sin = 0 nên cosx = 0 không thỏa mãn phương trình
Xét cosx ≠ 0 chia cả 2 vế cho cos3x ta được :
tan3x + 2 - 3tanx = 0
⇔ \(\left[{}\begin{matrix}tanx=1\\tanx=-2\end{matrix}\right.\)
d, cos2x - \(\sqrt{3}sin2x\) = 1 + sin2x
⇔ cos2x - sin2x - \(\sqrt{3}sin2x\) = 1
⇔ cos2x - \(\sqrt{3}sin2x\) = 1
⇔ \(2cos\left(2x+\dfrac{\pi}{3}\right)=1\)
⇔ \(cos\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}=cos\dfrac{\pi}{3}\)
e, cos3x + sin3x = 2cos5x + 2sin5x
⇔ cos3x (1 - 2cos2x) + sin3x (1 - 2sin2x) = 0
⇔ cos3x . (- cos2x) + sin3x . cos2x = 0
⇔ \(\left[{}\begin{matrix}sin^3x=cos^3x\\cos2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}sinx=cosx\\cos2x=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\cos2x=0\end{matrix}\right.\)
Giải các phương trình sau :
a) \(\cos x-\sqrt{3}\sin x=\sqrt{2}\)
b) \(3\sin3x-4\cos3x=5\)
c) \(2\sin x+2\cos x-\sqrt{2}=0\)
d) \(5\cos2x+12\sin2x-13=0\)
a) cosx - √3sinx = √2 ⇔ cosx - tan![]() sinx = √2
sinx = √2
⇔ cos![]() cosx - sin
cosx - sin![]() sinx = √2cos
sinx = √2cos![]() ⇔ cos(x +
⇔ cos(x + ![]() ) =
) = ![]()
⇔ 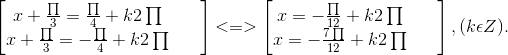
b) 3sin3x - 4cos3x = 5 ⇔ ![]() sin3x -
sin3x - ![]() cos3x = 1.
cos3x = 1.
Đặt α = arccos![]() thì phương trình trở thành
thì phương trình trở thành
cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α = ![]() + k2π
+ k2π
⇔ x = ![]() , k ∈ Z (trong đó α = arccos
, k ∈ Z (trong đó α = arccos![]() ).
).
c) Ta có sinx + cosx = √2cos(x - ![]() ) nên phương trình tương đương với
) nên phương trình tương đương với
2√2cos(x - ![]() ) - √2 = 0 ⇔ cos(x -
) - √2 = 0 ⇔ cos(x - ![]() ) =
) = ![]()
⇔ 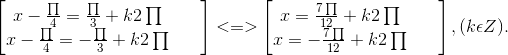
d) 5cos2x + 12sin2x -13 = 0 ⇔ ![]()
Đặt α = arccos![]() thì phương trình trở thành
thì phương trình trở thành
cosαcos2x + sinαsin2x = 1 ⇔ cos(2x - α) = 1
⇔ x = ![]() + kπ, k ∈ Z (trong đó α = arccos
+ kπ, k ∈ Z (trong đó α = arccos![]() ).
).
a/\(\sin3x+\cos2x=1+2\sin x\cos2x\)
b/\(\sin^3x+\cos^3x=2\left(\sin^5x+\cos^5x\right)\)
c/\(\dfrac{\tan x}{\sin x}-\dfrac{\sin x}{\cos x}=\dfrac{\sqrt{2}}{2}\)
d/\(\dfrac{\cos x\left(\cos x+2\sin x\right)+3\sin x\left(\sin x+\sqrt{2}\right)}{\sin2x-1}=1\)
e/\(\sin^2x+\sin^23x-2\cos^22x=0\)
f/\(\dfrac{\tan x-\sin x}{\sin^3x}=\dfrac{1}{\cos x}\)
g/\(\sin2x\left(\cos x+\tan2x\right)=4\cos^2x\)
h/\(\sin^2x+\sin^23x=\cos^2x+\cos^23x\)
k/\(4\sin2x=\dfrac{\cos^2x-\sin^2x}{\cos^6x+\sin^6x}\)
mọi người giải giúp em với em đang cần gấp ạ
giải phương trình: \(\dfrac{5\left(\sqrt{3}\sin x+\cos x\right)-\sqrt{3}\cos2x+\sin2x-6}{\cot x-1}=0\)
Giai các pt sau
1. \(\sqrt{3}\cos5x-2\sin3x.\cos2x-\sin x=0\)
4. \(\sin3x+\cos3x-\sin x+\cos x=\sqrt{2}\cos2x\)
6. \(\sin x+\cos x.\sin2x+\sqrt{3}\cos3x=2\left(\cos4x+\sin x^3\right)\)