1) Cho tam giác ABC, B = 60o, BC = 8cm; AB + AC = 12cm. Tính độ dài cạnh AB.
2) Cho đa thức bậc bốn f(x) có hệ số bậc cao nhất bằng 1 và f(1) = 10, f(2) = 20 và f(3) = 30. Tính f(10) + f(-6)
Làm được đến đâu thì làm nhé. Ai nhanh và đúng thì mình sẽ tick và add friends nhé. Thanks. Please help me!!!
DM
Những câu hỏi liên quan
Cho tam giác ABC, góc \(\widehat{B} \) = 60o, BC = 8cm, AB + AC = 12cm. Tính AB
Dựng \(AH\) vuông góc \(BC\). Đặt \(AB=x\Rightarrow AH=x.\sin60^0=\dfrac{x\sqrt{3}}{2};BH=x\cos60^0=\dfrac{x}{2}\)
\(\Rightarrow HC=BC-BH=8-\dfrac{x}{2};AC=12-x\)
Tam giác \(AHC\) vuông tại \(H\Rightarrow AC^2=AH^2+HC^2\Rightarrow\left(12-x\right)^2=\dfrac{3x^2}{4}+\left(8-\dfrac{x}{2}\right)^2\)
Giải phương trình trên ta được \(x=5\).
Vậy \(AB=5cm\).
Đúng 3
Bình luận (0)
. Cho tam giác ABC có Â = 60o , trực tâm H. Gọi M là điểm đối xứng với H qua BC.
a) CM : tam giác BHC+ tam giác BMC
b) Tính BMC ̂
cho tam giác abc có góc b =60o; ab=7cm; bc=15cm;vẽ ah vuông góc với bc(h thuộc bc). Lấy điểm m trên hc sao hm=hb
a)so sánh góc bac và góc acb
b)cm tam giác abm là tam giác đều
tam giác abc có phải là tam giác vuông không? vì sao
a) Xét ΔABC có
BA<BC(gt)
mà góc đối diện với cạnh BA là \(\widehat{ACB}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{BAC}>\widehat{ACB}\)(Quan hệ giữa cạnh và góc đối diện trong tam giác)
b) Xét ΔABH vuông tại H và ΔAMH vuông tại H có
HB=HM(gt)
AH chung
Do đó: ΔABH=ΔAMH(hai cạnh góc vuông)
Suy ra: BA=MA(hai cạnh tương ứng)
Xét ΔBAM có BA=MA(cmt)
nên ΔBAM cân tại A(Định nghĩa tam giác cân)
Xét ΔBAM cân tại A có \(\widehat{B}=60^0\)(gt)
nên ΔBAM đều(Dấu hiệu nhận biết tam giác đều)
Đúng 1
Bình luận (0)
Cho tam giác ABC có góc A = 60o, BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác đó
Áp dụng định lý Sin trong tam giác ABC ta có:
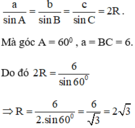
Vậy bán kính đường tròn ngoại tiếp tam giác bằng 2√3.
Đúng 0
Bình luận (0)
Bài 4. Cho tam giác ABC có góc A bằng 60o , đường cao BM và CN cắt nhau tại H. Nối AH cắt BC tại K. BiếtAC 8cm .a) Tính AN, NC và số đo các góc ABM và BHC.b) Chứng minh rằng AK ^ BC, MBC CAK .c) Gọi I là trung điểm của BC, Chứng minh rằng tam giác MIN đều.
Đọc tiếp
Bài 4. Cho tam giác ABC có góc A bằng 60o , đường cao BM và CN cắt nhau tại H. Nối AH cắt BC tại K. BiếtAC = 8cm .
a) Tính AN, NC và số đo các góc ABM và BHC.
b) Chứng minh rằng AK ^ BC, MBC = CAK .
c) Gọi I là trung điểm của BC, Chứng minh rằng tam giác MIN đều.
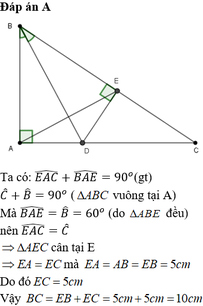
Cho tam giác ABC vuông tại A, có B ^ = 60 o , AB=5cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại E
Tính độ dài cạnh BC
A. 10cm
B. 5cm
C. 6cm
D. 8cm
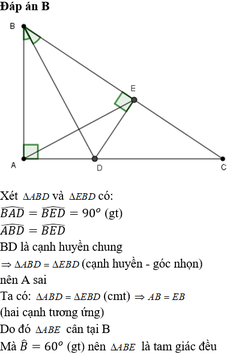
Bài 11. Cho tam giác ABC vuông tại A, có B̂ = 60o. Trên cạnh BC lấy điểm D sao cho BA=BD.
Tia phân giác của góc B cắt AC tại I.
a) Chứng minh: Tam giác BAD đều.
b) Chứng minh: Tam giác IBC cân.
c) Chứng minh: D là trung điểm của BC.
CAN GAP GAP
Cho tam giác ABC có A = 80o, B = 60o, C = 40o. Kẻ phân giác BD của tam giác.
Chứng minh rằng AB + AD = BC.
Trên BC lấy điểm E sao cho \(AB=BE\)
Dễ dàng chứng minh được \(\Delta ABD=\Delta EBD\left(c.g.c\right)\)
Do đó \(\widehat{BAC}=\widehat{BED}=80^0\)
Mà \(\widehat{BED}\) là góc ngoài tam giác DEC
\(\Rightarrow\widehat{BED}=\widehat{EDC}+\widehat{BCA}\\ \Rightarrow80^0=\widehat{EDC}+40^0\\ \Rightarrow\widehat{EDC}=40^0\Rightarrow\widehat{EDC}=\widehat{ECD}\left(=40^0\right)\\ \Rightarrow\Delta EDC.cân.tại.E\Rightarrow DE=EC\)
Vậy \(AB+AD=BE+EC=BC\)
Đúng 3
Bình luận (0)
Câu 6: Cho tam giác ABC vuông tại A, có B = 60o và AB = 5cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại E.
a/ Chứng minh:tam giác ABD = tam giác EBD.
b/ Chứng minh: tam giácABE là tam giác đều.
c/ Tính độ dài cạnh BC.
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên BA=BE
hay ΔBAE cân tại B
mà \(\widehat{ABE}=60^0\)
nên ΔBAE đều
Đúng 4
Bình luận (0)
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
\(\stackrel\frown{ABD}=\stackrel\frown{EBD}\)
\(BD\left(chung\right)\)
=> ΔABD=ΔEBD(c.h-gn)
:Ta có: ΔABD=ΔEBD(cmt)
nên BA=BE
=> ΔBAE cân tại B
mà \(\widehat{ABE}=60^o\)
=> ΔBAE đều(t/c tam giác cân)
Đúng 2
Bình luận (0)
TK
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
ˆABD=ˆEBDABD^=EBD^
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên BA=BE
hay ΔBAE cân tại B
mà ˆABE=600ABE^=600
nên ΔBAE đều
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, có
B
^
60
o
, AB5cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại EChọn câu đúng A.
∆
A
B
D
∆
B
E
D
B.
∆
A
B
E
là tam giác đều C.
∆
A
B
E
là tam giác vuông cân D. Cả A,B,C đều sai
Đọc tiếp
Cho tam giác ABC vuông tại A, có B ^ = 60 o , AB=5cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại E
Chọn câu đúng
A. ∆ A B D = ∆ B E D
B. ∆ A B E là tam giác đều
C. ∆ A B E là tam giác vuông cân
D. Cả A,B,C đều sai