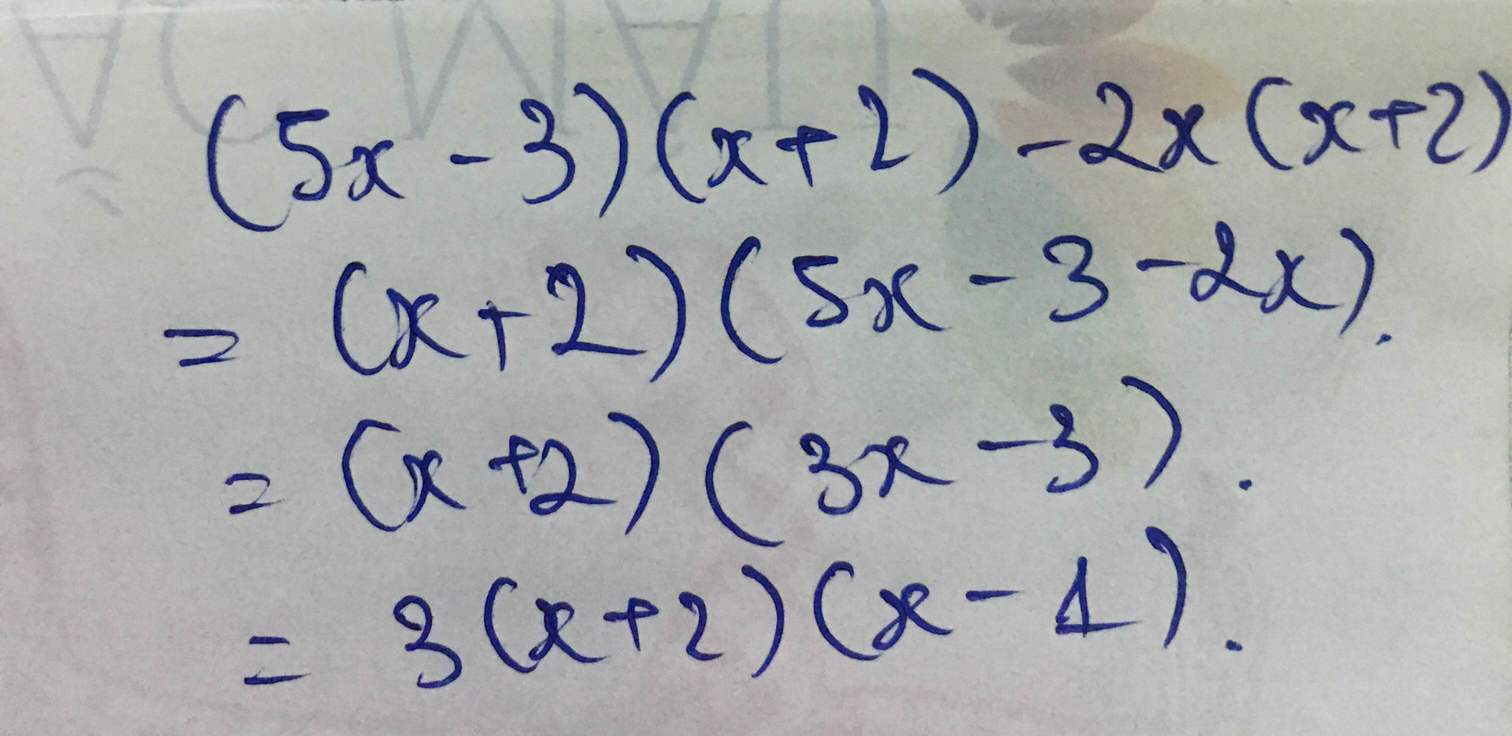Phân tích đa thức thành nhân tử: x^2+ 5x-2
DB
Những câu hỏi liên quan
Phân tích đa thức thành nhân tử (x^2+5x)^2-2(x^2+5x)-24
\(\left(x^2+5x\right)^2-2\left(x^2+5x\right)-24\\ =\left[\left(x^2+5x\right)^2-6\left(x^2+5x\right)\right]+\left[4\left(x^2+5x\right)-24\right]\\ =\left(x^2+5x\right)\left(x^2+5x-6\right)+4\left(x^2+5x-6\right)\\ =\left(x^2+5x-6\right)\left(x^2+5x+4\right)\\ =\left(x^2-x+6x-6\right)\left(x^2+4x+x+4\right)\\ =\left[x\left(x-1\right)+6\left(x-1\right)\right]+\left[x\left(x+4\right)+\left(x+4\right)\right]\\ =\left(x-1\right)\left(x+1\right)\left(x+4\right)\left(x+6\right)\)
Đúng 0
Bình luận (0)
(x2+5x)2−2(x2+5x)−24=[(x2+5x)2−6(x2+5x)]+[4(x2+5x)−24]=(x2+5x)(x2+5x−6)+4(x2+5x−6)=(x2+5x−6)(x2+5x+4)=(x2−x+6x−6)(x2+4x+x+4)=[x(x−1)+6(x−1)]+[x(x+4)+(x+4)]=(x−1)(x+1)(x+4)(x+6)
Đúng 1
Bình luận (0)
phân tích đa thức thành nhân tử x^3-5x^2+ 5x+ 1
\(x^3+5x^2+5x+1\)
\(=\left(x+1\right)\left(x^2+x+1\right)+5x\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+6x+1\right)\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử: (x^2+5x)^2+1õ^2+5x+24
x^2 - 5x - 1 phân tích đa thức thành nhân tử
\(=x^2-5x+\dfrac{25}{4}-\dfrac{29}{4}\)
\(=\left(x-\dfrac{5}{2}\right)^2-\dfrac{29}{4}\)
\(=\left(x-\dfrac{5}{2}-\dfrac{\sqrt{29}}{2}\right)\left(x-\dfrac{5}{2}+\dfrac{\sqrt{29}}{2}\right)\)
Đúng 0
Bình luận (0)
PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ BẰNG PHƯƠNG PHÁP ĐẶT NHÂN TỬ CHUNG
10)(5x-3)(x+2)-2x(x+2)
\(=\left(x+2\right)\left(5x-3-2x\right)\)
Đúng 1
Bình luận (1)
Phân tích đa thức thành nhân tử : x^2 - y^2 - 5x + 5y
\(=\left(x-y\right)\left(x+y\right)-5\left(x-y\right)=\left(x-y\right)\left(x+y-5\right)\)
Đúng 0
Bình luận (0)
\(=\left(x-y\right)\left(x+y\right)-5\left(x-y\right)=\left(x+y-5\right)\left(x-y\right)\)
Đúng 0
Bình luận (0)
\(x^2-y^2-5x+5y=\left(x+y\right)\left(x-y\right)-5\left(x-y\right)=\left(x-y\right)\left(x+y-5\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
phân tích đa thức thành nhân tử (thêm bớt cùng một hạng tử):
x^3 - 2x - 4
phân tích đa thức thành nhân tử (đặt biến phụ):
x^4 + 2x^3 + 5x^2 + 4x - 12
#)Giải :
\(x^3-2x-4\)
\(=x^3+2x^2-2x^2+2x-4x-4\)
\(=x^3+2x^2+2x-2x^2-4x-4\)
\(=x\left(x^2+2x+2\right)-2\left(x^2+2x+2\right)\)
\(=\left(x-2\right)\left(x^2+2x+2\right)\)
\(x^4+2x^3+5x^2+4x-12\)
\(=x^4+x^3+6x^2+x^3+x^2+6x-2x^2-2x-12\)
\(=x^2\left(x^2+x+6\right)+x\left(x^2+x+6\right)-2\left(x^2+x+6\right)\)
\(=\left(x^2+x+6\right)\left(x^2+x-2\right)\)
\(=\left(x^2+x+6\right)\left(x-1\right)\left(x+2\right)\)
Đúng 1
Bình luận (0)
Câu 1.
Đoán được nghiệm là 2.Ta giải như sau:
\(x^3-2x-4\)
\(=x^3-2x^2+2x^2-4x+2x-4\)
\(=x^2\left(x-2\right)+2x\left(x-2\right)+2\left(x-2\right)\)
\(=\left(x-2\right)\left(x^2+2x+2\right)\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử x^3 - 5x^2 + 5x - 5
Bài 1: Phân tích đa thức sau thànBài 1: Phân tích đa thức sau thành nhân tử a) x 2 – xy + x – y b) x 2 + 5x + 6 c) 2xy - x 2 - y 2 +16h nhân tử a) x 2 – xy + x – y b) x 2 + 5x + 6 c) 2xy - x 2 - y 2 +16
a) \(x^2-xy+x-y\)
\(=x\left(x-y\right)+\left(x-y\right)\)
\(=\left(x+1\right)\left(x-y\right)\)
b) \(x^2+5x+6\)
\(=x^2+2x+3x+6\)
\(=x\left(x+2\right)+3\left(x+2\right)\)
\(=\left(x+3\right)\left(x+2\right)\)
\(2xy-x^2-y^2+16\)
\(=16-\left(x-y\right)^2\)
\(=\left(4-x+y\right)\left(4+x-y\right)\)
Xem thêm câu trả lời