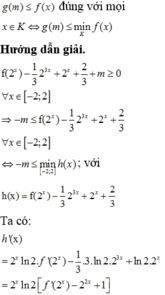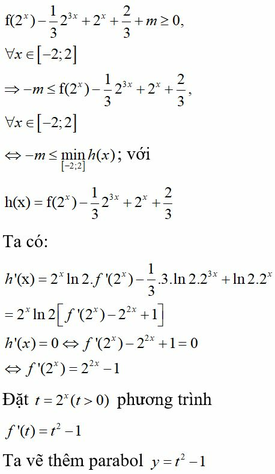Cho hàm số ✓x+m-2 + ✓2x -m =0. Tìm m để phương trình xác định với mọi x>1.
NT
Những câu hỏi liên quan
cho hàm số : y = √x−m+√2x−m−1x−m+2x−m−1 . tìm m để hàm số đã cho xác định trên tập số D và chứa mọi x > 0
Cho hàm số y = (3 – m)x2a) Tìm điều kiện của m để hàm số trên được xác định.b) Xác định m để hàm số đồng biến với mọi x < 0.c) Xác định m để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0.
a, ĐKXĐ để hàm được xác định : \(3-m\ne0\)
\(\Leftrightarrow m\ne3\)
b, - Với x < 0 để hàm số đồng biến thì : \(3-m< 0\)
\(\Leftrightarrow m>3\)
Vậy ...
c, - Để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0
\(\Leftrightarrow a>0\)
\(\Leftrightarrow3-m>0\)
\(\Leftrightarrow m< 3\)
Vậy ...
Đúng 2
Bình luận (0)
a) Để hàm số \(y=\left(3-m\right)x^2\) được xác định thì \(3-m\ne0\)
hay \(m\ne3\)
b) Để hàm số \(y=\left(3-m\right)x^2\) đồng biến với mọi x<0 thì \(3-m< 0\)
\(\Leftrightarrow m>3\)
c) Để y=0 là giá trị nhỏ nhất của hàm số tại x=0 thì 3-m>0
hay m<3
Đúng 2
Bình luận (0)
Cho hàm số yf(x) có đạo hàm liên tục trên R, đồ thị hàm số yf(x) như hình vẽ bên dưới. Cho bất phương trình
f
(
2
x
)
-
1
3
2
3
x
+
2
x
+
2
3
+
m
≥
0
; với m là tham số thực. Tìm điều kiện cần và đủ để bất...
Đọc tiếp
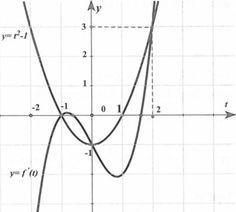
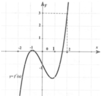
Cho hàm số y=f(x) có đạo hàm liên tục trên R, đồ thị hàm số y=f'(x) như hình vẽ bên dưới.
Cho bất phương trình
f
(
2
x
)
-
1
3
2
3
x
+
2
x
+
2
3
+
m
≥
0
; với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình
f
(
2
x
)
-
1
3
2
3
x
+
2
x
+
2
3
+
m
≥
0
đúng với mọi
x
∈
-
2
;
2
![]()
![]()
![]()
![]()
![]()
Giá trị của m để hàm số `y=\sqrt{x-m}+\sqrt{2x-m+1}` xác định với mọi `x>0`
Cho hàm số y (m - 1)x + m (d)a) Xác định m để hàm số trên là hàm số bậc nhâtb) Tìm m để hàm số trên là hàm số bậc nhất đồng biến, nghịch biến.c) Xác định m để đường thẳng ( d ): c1) Song song với đường thẳng có phương trình x - 2y 1. c2) Cắt trục hoành tại điểm A có hoành độ x 2. c3) Cắt đường thẳng (d): y 2x - 3 tại điểm nằm trên trục tung.
Đọc tiếp
Cho hàm số y = (m - 1)x + m (d)
a) Xác định m để hàm số trên là hàm số bậc nhât
b) Tìm m để hàm số trên là hàm số bậc nhất đồng biến, nghịch biến.
c) Xác định m để đường thẳng ( d ):
c1) Song song với đường thẳng có phương trình x - 2y = 1.
c2) Cắt trục hoành tại điểm A có hoành độ x = 2.
c3) Cắt đường thẳng (d'): y = 2x - 3 tại điểm nằm trên trục tung.
b: Để hàm số đồng biến thì m-1>0
hay m>1
Đúng 0
Bình luận (2)
Cho hàm số F(x) = (m + 1)x2 - 2mx + m - 2 (m là tham số). a) Tìm m để phương trình f(x) = 0 có hai nghiệm trái dấu? b) Tìm m để bất phương trình f(x) < 0 có một nghiệm đúng với mọi x.
Với thì PT có nghiệm (chọn)
Với thì là đa thức bậc 2 ẩn
có nghiệm khi mà
Tóm lại để có nghiệm thì
Cho hàm số y f (x) xác định, liên tục trên đoạn [-1;4]. Hàm số y f’(x) có đồ thị trên đoạn [-1;4] như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số thực m để bất phương trình
f
x
-
m
≥
0
nghiệm đúng với mọi x thuộc đoạn
3
2
;
10
3
A.
m
≤...
Đọc tiếp
Cho hàm số y = f (x) xác định, liên tục trên đoạn [-1;4]. Hàm số y = f’(x) có đồ thị trên đoạn [-1;4] như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số thực m để bất phương trình f x - m ≥ 0 nghiệm đúng với mọi x thuộc đoạn 3 2 ; 10 3
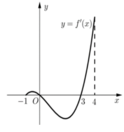
A. m ≤ f 3
B. m ≥ f 4
C. m ≤ f 3 2
D. m ≥ f 10 3
Cho hàm số yf(x)có đạo hàm liên tục trên
ℝ
, đồ thị hàm số yf’(x) như hình vẽ bên dưới.Cho bất phương trình
f
2
x
-
1
3
.
2
3
x
+
2
x
+
2
3
+
m
≥
0
với m là tham số thực. Tìm điều k...
Đọc tiếp
Cho hàm số y=f(x)có đạo hàm liên tục trên ℝ , đồ thị hàm số y=f’(x) như hình vẽ bên dưới.
Cho bất phương trình f 2 x - 1 3 . 2 3 x + 2 x + 2 3 + m ≥ 0 với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình f 2 x - 1 3 . 2 3 x + 2 x + 2 3 + m ≥ 0 đúng với mọi x ∈ - 2 ; 2
A. m ≥ - f 2
B. m ≥ - f 1 - 4 3
C. m ≤ - f 4 + 50 3
D. m ≤ - f 1 2 - 9 8
Cho phương trình :x^2-2left(m-1right)x+m^2-3m0a) Xác định m để phương trình có 2 nghiệm phân biệtb) Xác định m để phương trình có đúng 1 nghiệm âmc) Xác định m để phương trình có 1 nghiệm bằng 0. Tìm nghiệm còn lạid) Tìm hệ thức liên hệ giữa 2 nghiệm x1, x2 của phương trình không phụ thuộc và me) Xác định m để phương trình có 2 nghiệm thỏa mãn x1^2+x2^28
Đọc tiếp
Cho phương trình :
\(x^2-2\left(m-1\right)x+m^2-3m=0\)
a) Xác định m để phương trình có 2 nghiệm phân biệt
b) Xác định m để phương trình có đúng 1 nghiệm âm
c) Xác định m để phương trình có 1 nghiệm bằng 0. Tìm nghiệm còn lại
d) Tìm hệ thức liên hệ giữa 2 nghiệm x1, x2 của phương trình không phụ thuộc và m
e) Xác định m để phương trình có 2 nghiệm thỏa mãn \(x1^2+x2^2=8\)
x2-2(m-1)x+m2-3m=0
△'=[-(m-1)]2-1(m2-3m)=(m-1)2-(m2-3m)=m2-2m+1-m2+3m= m+1
áp dụng hệ thức Vi-ét ta được
x1+x2=2(m-1) (1)
x1*x2=m2-3m (2)
a) để PT có 2 nghiệm phân biệt khi m+1>0 <=> m>-1
b) để PT có duy nhất một nghiệm âm thì x1*x2 <0
Đúng 0
Bình luận (0)
e) Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)=2m-2\\x_1x_2=m^2-3m\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=8\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=8\)
\(\Leftrightarrow\left(2m-2\right)^2-2\cdot\left(m^2-3m\right)-8=0\)
\(\Leftrightarrow4m^2-8m+4-2m^2+6m-8=0\)
\(\Leftrightarrow2m^2-2m-4=0\)(1)
\(\Delta=\left(-2\right)^2-4\cdot2\cdot\left(-4\right)=4+32=36\)
Vì \(\Delta>0\) nên phương trình (1) có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{2-\sqrt{36}}{4}=\dfrac{2-6}{4}=-1\\m_2=\dfrac{2+\sqrt{36}}{4}=\dfrac{2+6}{4}=2\end{matrix}\right.\)
Vậy: Để phương trình có hai nghiệm phân biệt thỏa mãn \(x_1^2+x_2^2=8\) thì \(m\in\left\{-1;2\right\}\)
Đúng 1
Bình luận (0)
Giải và biện luận các phương trình sau (với m là tham số):
a) mx – x – m + 2 = 0
\(b) m^2x + 3mx – m^2 + 9 = 0 \)
\(c) m^3x – m^2 - 4 = 4m(x – 1)\)
2) Cho phương trình ẩn x: . Hãy xác định các giá trị của k để phương trình trên có nghiệm x = 2.
\(mx-x-m+2=0\)
\(x\left(m-1\right)=m-2\)
Nếu m=1 ⇒ \(0x=-1\) (vô nghiệm)
Nếu m≠1 ⇒ \(x=\dfrac{m-2}{m-1}\)
Vậy ...
Đúng 2
Bình luận (0)