Cho ΔABC nhọn; M,N lần lượt là trung điểm của AB và AC.Gọi AH là đường cao (HϵBC). Đoản thẳng MN cắt AH tại K.
a) C/m tg MNCB là hình thang
b) C/m tg KNCH là hình thang
c) Tg KHBM là hình thang vuông
Cho ΔABC nhọn nội tiếp (O;12),AB=8;AC=15.Khi đó độ dài đường cao AH của ΔABC là
A.5 B.10 C.7 D.3
Cho ΔABC nhọn nội tiếp (O) và AB<AC.Vẽ đường cao CD của ΔABC và đường kính AM.Hạ CE⊥AM tại E , H là trực tâm của ΔABC.Chứng minh DE.BC=DC.BM
cho ΔABC nhọn,hai đườngcao bd và ce
biết Å=60σ,Sabc=120 cm2.tính Sade
XétΔABD vuông tại D và ΔACE vuông tại E có
góc BAD chung
Do đó: ΔABD\(\sim\)ΔACE
Suy ra: AD/AE=AB/AC
hay AD/AB=AE/AC
Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
Do đó; ΔADE\(\sim\)ΔABC
Suy ra: \(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2=\dfrac{1}{4}\)
hay \(S_{ADE}=30\left(cm^2\right)\)
* Cho ΔABC vuông tại A, biết AC= 12cm, BC=15cm
a. Giải tam giác ABC
b. Tính độ dài đường cao AH, đường phân giác AD của ΔABC
* Cho ΔABC có 3 góc nhọn, kẻ đường cao AH.
a. CM: sinA+cos A>1
b. CM: BC=AH. (cotgB+cotgC)
c. Biết AH=6cm, góc B=\(60^0\), góc C=\(45^0\). Tính diện tích ΔABC
Bài 2:
b: \(AH\cdot\left(\cot\widehat{B}+\cot\widehat{C}\right)\)
\(=AH\cdot\left(\dfrac{BH}{AH}+\dfrac{CH}{AH}\right)\)
\(=AH\cdot\dfrac{BC}{AH}=BC\)
Cho ΔABC nhọn nội tiếp đường tròn (O) có H là trực tâm của ΔABC. Gọi R là điểm đối xứng của O qua BC. Chứng minh rằng R là tâm đường tròn ngoại tiếp ΔBHC.
Giúp mình với ạ!!!
Cho tam giác nhọn ABC có 3 đường cao AB, BE, CF. Biết AD=BE=CF
Chứng minh rằng ΔABC đều
Xét ΔAFC vuông tại F và ΔAEB vuông tại E có
CF=BE
góc ACF=gócABE
=>ΔAFC=ΔAEB
=>AC=AB
Xét ΔCEB vuông tại E và ΔCDA vuông tại D có
EB=DA
góc C chung
=>ΔCEB=ΔCDA
=>CB=CA=AB
=>ΔABC đều
cho ΔABC có 3 góc nhọn (ab<ac),các đường cao ak,bd,ce cắt nhau tại h.gọi m,n lần lượt là giao điểm của de với ah và bc.CMR;
a) ΔABD đồng dạng ΔACE
b) CA.CD=CB.Ck
c) ΔKDC đồng dạng ΔABc
a, Xét tam giác ABD và tam giác ACE
^A _ chung
^ADB = ^AEC = 900
Vậy tam giác ABD ~ tam giác ACE (g.g)
b, Xét tam giác CBD và tam giác CAK ta có
^C _ chung
^CDB = ^CKA = 900
Vậy tam giác CDB ~ tam giác CKA (g.g)
\(\dfrac{CD}{CK}=\dfrac{CB}{CA}\Rightarrow CD.CA=CB.CK\)
c, Xét tam giác KDC và tam giác ABC
^C _ chung
\(\dfrac{DC}{BC}=\dfrac{KC}{AC}\)( tỉ lệ thức tỉ số đồng dạng )
Vậy tam giác KDC ~ tam giác ABC (c.g.c)
Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. Chọn khẳng định đúng?
A. AD.AE = AB.AF
B. AD.AE = AB.AG = AC.AF
C. AD.AE = AC.GA
D. AD.AE = AB.AF = AC.AG
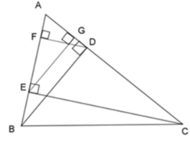
Từ câu trước ta có: A E A B = A G A D => AE.AD = AB.AG (1)
Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)
=> => AF.AC = AE.AD (2)
Từ (1) và (2) ta có: AD.AE = AB.AG = AC.AF
Đáp án: B
Cho ΔABC nhọn. Các đường cao AH và BD cắt nhau tại E.
a, Chứng minh: ΔAHC ~ ΔBDC
Vẽ hộ mình hình nữa nha
Xét ΔAHC vuông tại H và ΔBDC vuông tại D có
góc C chung
Do đó: ΔAHC\(\sim\)ΔBDC