cho hàm số y=f(x)= (2m-3)x+m-5
Tìm m để f(1) > f(2) .
a) Để điểm A(m;2m+1) thuộc đồ thị hàm số (1) thì:
2m+1=3m+5 <=> m=-4
b) Ta có:
\(f\left(\dfrac{-1}{2}\right)+f\left(3\right)=3.\dfrac{-1}{2}+5+3.3+5\\ =\dfrac{35}{2}\)
Cho hàm số f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y=f(|x|) có 5 cực trị
A. - 10 < m < 5 4
B. - 2 < m < 5
C. - 2 < m < 5 4
D. 5 4 < m < 2
a) (1- x2). ( 4x+5/x-1 - 9/x-1)
b. x2 + xy - 2x - 2y
Câu 5. Cho hàm số: y = (2m+1)x - 3
a. Với m=3. Tính f (-3); f(0)
b. Tìm m để điểm A(2; 3) thuộc đồ thị hàm số.
c. Vẽ đồ thị hàm số với m= 1
d. Tìm điều kiện để hàm số là hàm bậc nhất.
e. Tìm m để hàm số song song với đường thẳng y= 5x+1
Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
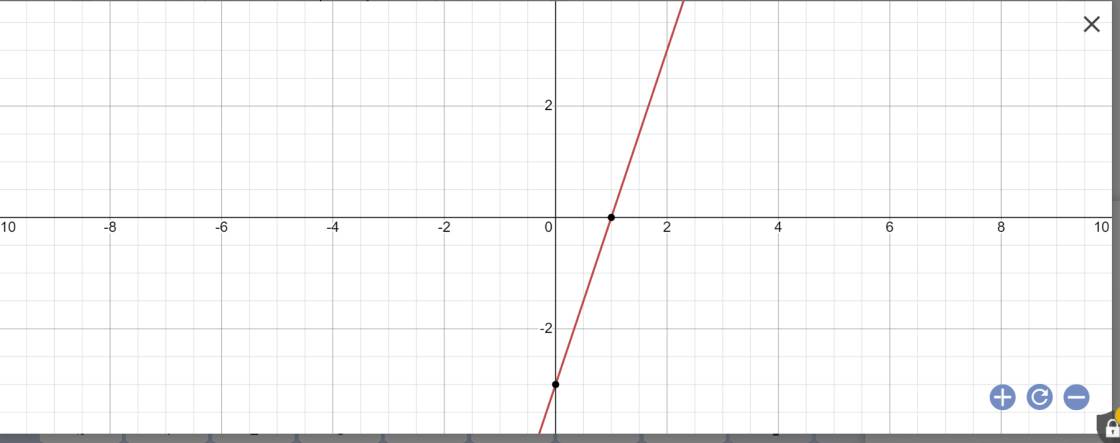
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2
Cho hàm số y = f ( x ) = x 3 - ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tất cả các giá trị của tham số m để hàm số y=f(|x|) có 5 điểm cực trị
A. 5 4 < m ≤ 2
B. - 2 < m < 5 4
C. - 5 4 < m < 2
D. 5 4 < m < 2
1.tìm m để phương trình \(x^2+\dfrac{1}{x^2}-2m\left(x+\dfrac{1}{x}\right)+1+2m=0\left(x\ne0\right)\) có nghiệm
2. cho hàm số y=f(x)=\(x^2-4x+3\)
tìmcác giá trị nguyên của m để
\(f^2\left(\left|x\right|\right)+\left(m-2\right)f\left(\left|x\right|\right)+m-3=0\) có 6 nghiệm phân biệt
\(1.x^2+\dfrac{1}{x^2}-2m\left(x+\dfrac{1}{x}\right)+1+2m=0\left(1\right)\)\(đặt:x^2+\dfrac{1}{x^2}=t\)
\(x>0\Rightarrow t\ge2\sqrt{x^2.\dfrac{1}{x^2}}=2\)
\(x< 0\Rightarrow-t=-x^2+\dfrac{1}{\left(-x^2\right)}\ge2\Rightarrow t\le-2\)
\(\Rightarrow t\in(-\infty;-2]\cup[2;+\infty)\left(2\right)\)
\(\Rightarrow\left(1\right)\Leftrightarrow t^2-2mt+2m-1=0\)
\(\Leftrightarrow\left(t-1\right)\left(t-2m+1\right)=0\Leftrightarrow\left[{}\begin{matrix}t=1\notin\left(2\right)\\t=2m-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2m-1\le-2\\2m-1\ge2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m\le-\dfrac{1}{2}\\m\ge\dfrac{3}{4}\end{matrix}\right.\)
\(2.\) \(f^2\left(\left|x\right|\right)+\left(m-2\right)f\left(\left|x\right|\right)+m-3=0\left(1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}f\left(\left|x\right|\right)=-1\\f\left(\left|x\right|\right)=3-m\end{matrix}\right.\)
\(dựa\) \(vào\) \(đồ\) \(thị\) \(f\left(\left|x\right|\right)\) \(\Rightarrow f\left(\left|x\right|\right)=-1\) \(có\) \(2nghiem\) \(pb\)
\(\left(1\right)có\) \(6\) \(ngo\) \(pb\Leftrightarrow\left\{{}\begin{matrix}-1< 3-m< 3\\3-m\ne-1\\\end{matrix}\right.\)\(\Leftrightarrow0< m< 4\)
\(\Rightarrow m=\left\{1;2;3\right\}\)
Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình vẽ dưới đây
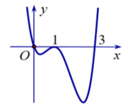
Tìm m để hàm số y = f( x 2 -2m) có ba điểm cực trị
A. m ∈ (- 3 2 ;0]
B. m ∈ (3;+ ∞ )
C. m ∈ [0; 3 2 ]
D. m ∈ (- ∞ ;0)
Chọn A.
Theo đồ thị ta có: f'(x) > 0 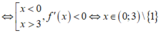
Ta có: ![]()
Cho y' = 0
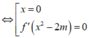
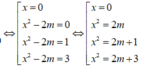
Để hàm số có 3 điểm cực trị thì phương trình y' = 0 phải có 3 nghiệm bội lẻ
Ta thấy x = 0 là một nghiệm bội lẻ
Dựa vào đồ thị của y = f'(x) ta thấy x = 1 là nghiệm bội lẻ (không đổi dấu), do đó ta không xét trường hợp ![]()
Suy ra để hàm số có 3 điểm cực trị thì
TH1: x 2 = 2m có 2 nghiệm phân biệt khác 0 và x 2 = 2m + 3 vô nghiệm hoặc có nghiệm kép bằng 0
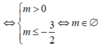
TH2. x 2 = 2m + 3 có 2 nghiệm phân biệt khác 0 và x 2 = 2m vô nghiệm hoặc có nghiệm kép bằng 0
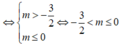
Vậy hàm số của 3 điểm cực trị khi 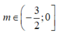
Cho hàm số y = f(x). Hàm số y = f’(x) có đồ thị như hình vẽ dưới đây:
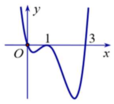 Tìm m để hàm số y = f(x2 – 2m) có ba điểm cực trị.
Tìm m để hàm số y = f(x2 – 2m) có ba điểm cực trị.
A. m ∈ ( - 3 2 ; 0 ]
B. m ∈ 3 ; + ∞
C. m ∈ 0 ; 3 2
D. m ∈ - ∞ ; 0
cho hàm số y= f(x)=(m-3)x + m-2 a)tìm m để hàm số trên là hàm số đồng biến b) tìm m biết f(-1)=1
a: Để hàm số đồng biến thì m-3>0
hay m>3
b: Thay x=-1 và y=1 vào (d), ta được:
-m+3+m-2=1
hay 1=1(đúng)
Cho hàm số y = f(x) = -x3 + (2m – 1)x2 – (2 – m)x – 2. Tìm m để đồ thị hàm số có cực đại và cực tiểu?
A. m ∈ (-1; +∞)
B. m ∈ (-1; 5/4)
C. m ∈ (-∞; -1)
D. m ∈ (-∞; -1) ∪ (5/4; +∞)
Đáp án D.
y = -x3 + (2m – 1)x2 – (2 – m)x – 2
TXĐ: D = R
y' = -3x2 + 2(2m – 1) – 2 + m
Đồ thị hàm số có cực đại và cực tiểu <=> Pt y’ = 0 có hai nghiệm phân biệt
<=> Δ’ = (2m – 1)2 + 3(-2 + m) > 0 <=> 4m2 – m – 5 > 0 <=> m ∈ (-∞; -1) ∪ (5/4; +∞)
cho hàm số y = f(x)=(2m-1)*x
a Tìm m biết đồ thị hàm số đi qua A(1;-3)
b. Tìm m biết f(2)=5
mình đang rất gấp ai làm nhanh đúng mình tick cho .