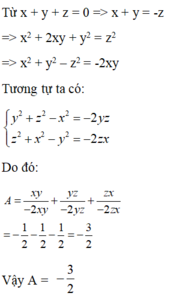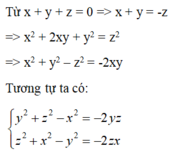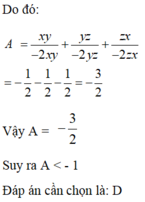Cho x,y,z≥0, thỏa mãn: 12x+10y+15z≤60. Tìm GTLN của T=x2+y2+z2 - 4x - 4y - z
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
AJ
Những câu hỏi liên quan
Cho x, y. z là các số thực không âm thỏa mãn \(12x+10y+15z\le60\). Tìm GTLN của \(P=x^2+y^2+z^2-4x-4y-z\)
Xét \(5P-\left(12x+10y+15z\right)=5x^2-32x+5y^2-30y+5z^2-20z.\)
\(=5x\left(x-6,4\right)+5y\left(y-6\right)+5z\left(z-4\right).\)(1)
Mà \(x,y,z\ge0\)nên từ \(12x+10y+15z\le60\)suy ra \(\hept{\begin{cases}12x\le60\\10y\le60\\15z\le60\end{cases}\Leftrightarrow\hept{\begin{cases}x\le5\\y\le6\\z\le4\end{cases}\Rightarrow}}\hept{\begin{cases}x-6,4< 0\\y-6\le0\\z-4\le0\end{cases}\Rightarrow\hept{\begin{cases}x\left(x-6,4\right)\le0\\y\left(y-6\right)\le0\\z\left(z-4\right)\le0\end{cases}.}}\)(2)
Từ (1) và (2) suy ra \(5P-\left(12x+10y+15z\right)\le0\)
\(\Rightarrow P\le\frac{12x+10y+15z}{5}\le\frac{60}{5}=12.\)
Vậy GTLN của P=12, Dấu '=' xảy ra khi \(\hept{\begin{cases}x\left(x-6,4\right)=y\left(y-6\right)=z\left(z-4\right)=0\\12x+10y+15z=60\end{cases}\Leftrightarrow\orbr{\begin{cases}x=y=0;z=4\\x=z=0;y=6\end{cases}.}}\)
Đúng 1
Bình luận (0)
Các số thực a,b,c,x,y,z thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
+
4
c
+
4
0
và
x
2
+
y
2
+
z
2
-
4
x
+
4
y
+
4...
Đọc tiếp
Các số thực a,b,c,x,y,z thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 c + 4 = 0 và x 2 + y 2 + z 2 - 4 x + 4 y + 4 = 0 . Tìm GTLN của S = a - x 2 + b - y 2 + z - c 2 .
![]()
![]()
![]()
![]()
mọi người ơi cho mình hỏi bài này tí.
cho x,y,z \(\ge\)0 thỏa mãn 12x+10y+15z\(\le\)60
Tìm max T=\(x^2+y^2+z^2-4x-4y-z\)
cho x, y, z ≥ 0 thỏa mãn x + y + z =6. Tìm GTNN và GTLN của
A = x2 + y2 + z2
Bạn tham khảo lời giải tại đây:
cho \(x,y,z\ge0\) thỏa mãn \(x y z=6\). tìm GTLN và GTNN của biểu thức \(A=x^2 y^2 z^2\) - Hoc24
Đúng 0
Bình luận (0)
cho x,y,z>0 thỏa mãn: x2+yz+z2=1-\(\dfrac{3x^2}{z}\).
Tìm GTNN và GTLN của P= x+y+z
Cho x; y; z ≠ 0 thỏa mãn x + y + z 0. Tính giá trị biểu thức: A
x
y
x
2
+
y
2
−
z
2
+
y
z
y
2
+...
Đọc tiếp
Cho x; y; z ≠ 0 thỏa mãn x + y + z = 0. Tính giá trị biểu thức: A = x y x 2 + y 2 − z 2 + y z y 2 + z 2 − x 2 + z x z 2 + x 2 − y 2
A. A = 1 2
B. A = - 1 2
C. A = - 3 2
D. A = 3 2
cho x y z là các số thực dương thỏa mãn x + y + z = 3.Tìm GTLN của A= xy/căn(z2+3) + yz/căn(x2+3) + zx/căn(y2+3)
Cho x; y; z ≠ 0 thỏa mãn x + y + z 0. Chọn câu đúng về biểu thức
A
x
y
x
2
+
y
2
−
z
2
+
y
z
y
2...
Đọc tiếp
Cho x; y; z ≠ 0 thỏa mãn x + y + z = 0. Chọn câu đúng về biểu thức A = x y x 2 + y 2 − z 2 + y z y 2 + z 2 − x 2 + z x z 2 + x 2 − y 2
A. A < -2
B.0 < A < 1
C. A > 0
D. A < -1
cho x y z và 1/x+1/y+1/z=2016. Tìm GTLN của P=(x+y/x2+y2)+(y+z/y2+z2)+(z+x/z2+x2)
Xem chi tiết
Ta có : \(x^2+y^2\ge2xy\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge\left(x+y\right)^2\)
\(\Leftrightarrow x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\)
Áp dụng vào bài toán có :
\(P\le\frac{x+y}{\frac{\left(x+y\right)^2}{2}}+\frac{y+z}{\frac{\left(y+z\right)^2}{2}}+\frac{z+x}{\frac{\left(z+x\right)^2}{2}}\) \(=\frac{2}{x+y}+\frac{2}{y+z}+\frac{2}{z+x}=\frac{1}{2}\left(\frac{4}{x+y}+\frac{4}{y+z}+\frac{4}{z+x}\right)\)
Áp dụng BĐT Svacxo ta có :
\(\frac{4}{x+y}\le\frac{1}{x}+\frac{1}{y}\), \(\frac{4}{y+z}\le\frac{1}{y}+\frac{1}{z}\), \(\frac{4}{z+x}\le\frac{1}{z}+\frac{1}{x}\)
Do đó : \(P\le\frac{1}{2}\left[2.\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\right]=2016\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=z=\frac{1}{672}\)
P/s : Dấu "=" không chắc lắm :))
thanks bạn mình hiểu sương sương rồi:))