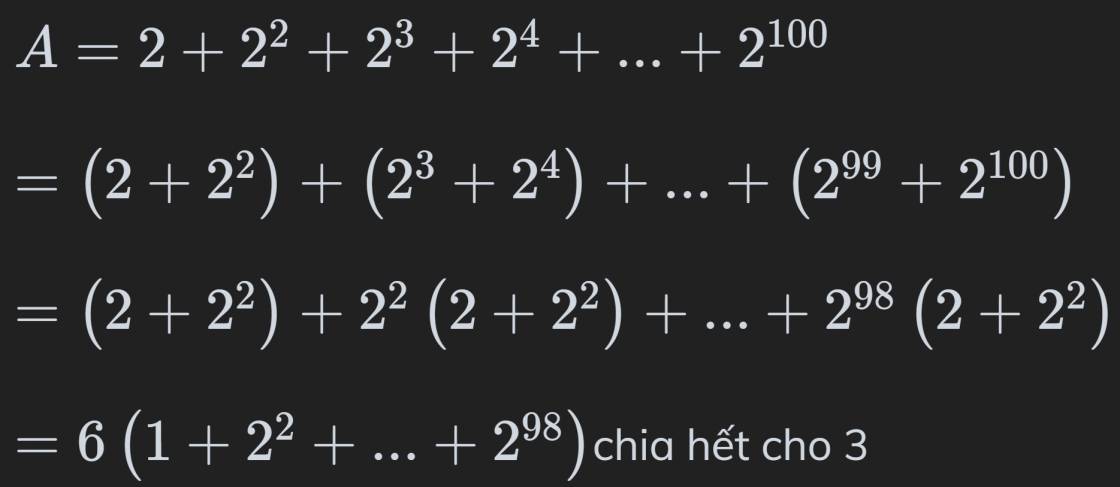A=5+52+53+54+.......+519+520.Hãy chứng minh A chia hết cho 30
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
ND
Những câu hỏi liên quan
Chứng tỏ: C = 5 +52+53+...+519+520 chia hết cho 13
\(C=\left(5+5^2+5^3+5^4\right)+\left(5^5+5^6+5^7+5^8\right)...+\left(5^{17}+5^{18}+5^{19}+5^{20}\right)\\ C=5\left(1+5+5^2+5^3\right)+5^5\left(1+5+5^2+5^3\right)...+5^{17}\left(1+5+5^2+5^3\right)\\ C=5\cdot156+5^5\cdot156+...+5^{17}\cdot156\\ C=156\left(5+5^5+...+5^{17}\right)\\ C=12\cdot13\left(5+5^5+...+5^{17}\right)⋮17\)
Đúng 0
Bình luận (0)
(5 +53)+(52+54)...+(518+520)
5(1+52)+52(1+52)+...+518(1+52)
(1+52)(5+52+...+518)
26(5+52+...+518)⋮13
vậy (5 +53)+(52+54)...+(518+520)⋮13
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho C=5+52+53+54+...+520 chứng minh rằng:
a)C chia hết cho 5 b) C chia hết cho 6 c) C chia hết cho 13
\(a,C=5+5^2+5^3+5^4+\cdot\cdot\cdot+5^{20}\)
\(=5\left(1+5+5^2+\cdot\cdot\cdot+5^{19}\right)\)
Ta thấy: \(5\left(1+5+5^2+\cdot\cdot\cdot+5^{19}\right)⋮5\)
nên \(C⋮5\)
\(b,C=5+5^2+5^3+5^4\cdot\cdot\cdot+5^{20}\)
\(=\left(5+5^2\right)+\left(5^3+5^4\right)+\cdot\cdot\cdot+\left(5^{19}+5^{20}\right)\)
\(=5\left(1+5\right)+5^3\left(1+5\right)+\cdot\cdot\cdot+5^{19}\left(1+5\right)\)
\(=5\cdot6+5^3\cdot6+\cdot\cdot\cdot+5^{19}\cdot6\)
\(=6\cdot\left(5+5^3+\cdot\cdot\cdot+5^{19}\right)\)
Ta thấy: \(6\cdot\left(5+5^3+\cdot\cdot\cdot+5^{19}\right)⋮6\)
nên \(C⋮6\)
\(c,C=5+5^2+5^3+5^4+\cdot\cdot\cdot+5^{20}\)
\(=\left(5+5^3\right)+\left(5^2+5^4\right)+\cdot\cdot\cdot+\left(5^{17}+5^{19}\right)+\left(5^{18}+5^{20}\right)\)
\(=5\left(1+5^2\right)+5^2\left(1+5^2\right)+\cdot\cdot\cdot+5^{17}\cdot\left(1+5^2\right)+5^{18}\left(1+5^2\right)\)
\(=5\cdot26+5^2\cdot26+\cdot\cdot\cdot+5^{17}\cdot26+5^{18}\cdot26\)
\(=26\cdot\left(5+5^2+\cdot\cdot\cdot+5^{17}+5^{18}\right)\)
Ta thấy: \(26\cdot\left(5+5^2+\cdot\cdot\cdot+5^{17}+5^{18}\right)⋮13\)
nên \(C⋮13\)
#\(Toru\)
Đúng 3
Bình luận (0)
a, ta có
C = 5 + 5^2 + 5^3 + 5^4 + ... + 5^20
=> C = 5 . ( 1 + 5 + 5^2 + 5^3 + ... + 5^19 )
=> C chia hết cho 5
b,
C = 5 + 5^2 + 5^3 + 5^4 + ... + 5^20
=> C = 5 . ( 1 + 5 ) + 5^3 . ( 1 + 5 ) + ... + 5^19 . ( 1 + 5 )
=> C = 5 . 6 + 5^3 . 6 + ... + 5^19 . 6
=> C = 6 . ( 5 + 5^3 + ... + 5^19 )
=> C chia hết cho 6
c,
C = 5 + 5^2 + 5^3 + ... + 5^20
=> C = (5 + 5^2 + 5^3 + 5^4 ) + ... + (5^17 + 5^18 + 5^19 + 5^20 )
=> C = 5 . ( 1 + 5 + 5^2 + 5^3 ) + ... + 5^17 . ( 1+ 5 + 5^2 +5^3)
=> C = 5 . 156 + 5^5 . 156 + ...+ 5^17 . 156
=> C = 5 . 12 . 13 + 5^5 . 12 . 13 + ... + 5^17 . 12 . 13
=> C = 13 . ( 5 . 12 + 5^5 . 12 + ... + 5^17 . 12 )
=> C chia hết cho 13
C = 5 + 5^2 + 5^3 + 5^4 + ... + 5^20
=> C = 5 . ( 1 + 5 + 5^2 + 5^3 + ... + 5^19 )
=> C chia hết cho 5
b,
C = 5 + 5^2 + 5^3 + 5^4 + ... + 5^20
=> C = 5 . ( 1 + 5 ) + 5^3 . ( 1 + 5 ) + ... + 5^19 . ( 1 + 5 )
=> C = 5 . 6 + 5^3 . 6 + ... + 5^19 . 6
=> C = 6 . ( 5 + 5^3 + ... + 5^19 )
=> C chia hết cho 6
c,
C = 5 + 5^2 + 5^3 + ... + 5^20
=> C = (5 + 5^2 + 5^3 + 5^4 ) + ... + (5^17 + 5^18 + 5^19 + 5^20 )
=> C = 5 . ( 1 + 5 + 5^2 + 5^3 ) + ... + 5^17 . ( 1+ 5 + 5^2 +5^3)
=> C = 5 . 156 + 5^5 . 156 + ...+ 5^17 . 156
=> C = 5 . 12 . 13 + 5^5 . 12 . 13 + ... + 5^17 . 12 . 13
=> C = 13 . ( 5 . 12 + 5^5 . 12 + ... + 5^17 . 12 )
=> C chia hết cho 13
Đúng 1
Bình luận (0)
a) Chứng minh: B = 31 + 32 + 33 + 34 + … + 32010 chia hết cho 4.
b) Chứng minh: C = 51 + 52 + 53 + 54 + … + 52010 chia hết cho 31.
c) Cho S=17+52+53+54+ ... +52010 . Tìm số dư khi chia S cho 31.
\(B=3+3^2+3^3+3^4+...+3^{2009}+3^{2010}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{2009}\left(1+3\right)\)
\(=4.\left(3+3^3+...+3^{2009}\right)\)
⇒ \(B\) ⋮ 4
Đúng 3
Bình luận (0)
b: \(C=5\left(1+5+5^2\right)+...+5^{2008}\left(1+5+5^2\right)=31\cdot\left(5+...+5^{2008}\right)⋮31\)
Đúng 2
Bình luận (0)
B= 5 +52+53+...+520 chia hết cho 30
Cứu tôi với :<
\(B=5+5^2+5^3+...+5^{20}\\ B=\left(5+5^2\right)+5^2\left(5+5^{\text{2}}\right)+.....+5^{18}\left(5+5^2\right)\\ B=30+5^2\cdot30+...+5^{18}\cdot30\\ B=30\left(1+5^2+...+5^{18}\right)\\ =>30\left(1+5^2+...+5^{18}\right)⋮30\\ CMR:B⋮30\)
Đúng 2
Bình luận (0)
Ba bạn Lan Thu Cúc mặc ba cái áo màu trắng vàng Hồng và cài 3 cái nơ cùng màu trắng và Hồng biết rằng
chỉ có bạn Lan là có màu áo và màu nơ giống nhau B màu áo và màu nơ của Thu đều không phải làm trắng C Cúc cài nơ màu hồng Hãy xác định xem bạn nào mặc màu gì và cái nơ màu gì
Đúng 0
Bình luận (0)
chứng minh A = 52+53+54+...+52021 chia hết cho 6
\(A=\left(5^2+5^3\right)+\left(5^4+5^5\right)+...+\left(5^{2020}+5^{2021}\right)\\ =5^2.\left(1+5\right)+5^4.\left(1+5\right)+...+5^{2020}.\left(1+5\right)\\ =5^2.6+5^4.6+...+5^{2020}.6\\ =6.\left(5^2+5^4+...+5^{2020}\right)⋮6\)
Đúng 4
Bình luận (0)
Cho M = 51 + 52 + 53 ... + 519 + 520 + 521
Chứng minh M là bội của 31
Giúp e nha mọi người ![]()
M = 51 + 52 + 53 + ... + 519 + 520 + 521
M = (51 + 52 + 53) + (54 + 55 + 56 ) + ... + (519 + 520 + 521)
M = 5( 1 + 5 + 52) + 54(1 + 5 + 52) + ... + 519(1 + 5 + 52)
M = 5.31 + 54.31 + ... + 519.31
M = 31(5 + 54 + ... + 519) ⋮ 31 (ĐPCM)
Đúng 0
Bình luận (0)
a. Chứng minh A=21+22+23+24+...+2100 chia hết cho 3
b. Chứng minh B=31+32+33+34+...+299chia hết cho 13
c. Chứng minh C=51+52+53+54+...+5105 chia hết cho 6 và 31
Câu 1 : 1+52+53+54+...+5404:31
Câu 2 : a ) Chứng minh : Trong 3 Số tự nhiên liên tiếp có một số chia hết cho 3
b ) Chứng minh : Trong 5 Số tự nhiên liên tiếp có một số chia hết cho 5
Câu 1 : 1+52+53+54+...+5404:31
Câu 2 : a ) Chứng minh : Trong 3 Số tự nhiên liên tiếp có một số chia hết cho 3
b ) Chứng minh : Trong 5 Số tự nhiên liên tiếp có một số chia hết cho 5
Chứng minh rằng C = 5 + 5 2 + 5 3 + ... + 5 8 chia hết cho 30
Sơ đồ con đường |
Lời giải chi tiết |
|
Ta có: C = 5 + 5 2 + 5 3 + ... + 5 8 = 5 + 5 2 + 5 3 + 5 4 + 5 5 + 5 6 + 5 7 + 5 8 = 30 + 5 2 5 + 5 2 + 5 4 5 + 5 2 + 5 6 5 + 5 2 = 30 + 5 2 5 + 5 2 + 5 4 5 + 5 2 + 5 6 5 + 5 2 = 30 + 5 2 .30 + 5 4 .30 + 5 6 .30 = 30. 1 + 5 2 + 5 4 + 5 6 Áp dụng tính chất chia hết của một tích ta có: 30 ⋮ 30 ⇒ 30. 1 + 5 2 + 5 4 + 5 6 ⋮ 30 ⇒ C = 30. 1 + 5 2 + 5 4 + 5 6 ⋮ 30 |
Đúng 1
Bình luận (0)