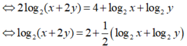Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
BB
Những câu hỏi liên quan
Cho x; y 0 và x2 + 4y2 12xy . Khẳng định nào sau đây là khẳng định đúng? A. log2
x
+
2
y
4
log2x-log2y B. log2(x+2y)2+
1
2
(log2x+log2y) C. log2(x + 2y) log2x+log2y+1 D. 4log2( x + 2y) log2x + log2y.
Đọc tiếp
Cho x; y > 0 và x2 + 4y2 = 12xy . Khẳng định nào sau đây là khẳng định đúng?
A. log2 x + 2 y 4 =log2x-log2y
B. log2(x+2y)=2+ 1 2 (log2x+log2y)
C. log2(x + 2y) = log2x+log2y+1
D. 4log2( x + 2y) = log2x + log2y.
Chọn B.
Vì x2 + 4y2 = 12xy nên (x + 2y)2 = 16xy hay log2( x + 2y) 2= log216xy
Do đó: 2log2(x + 2y) = 4 + log2x + log2y
Vậy ![]()
Đúng 0
Bình luận (0)
Cho
x
;
y
0
v
à
x
2
+
4
y
2
12
x
y
.
Khẳng định nào sau đây là khẳng định đúng ? A.
log
2
x
+
2
y
4...
Đọc tiếp
Cho x ; y > 0 v à x 2 + 4 y 2 = 12 x y . Khẳng định nào sau đây là khẳng định đúng ?
A. log 2 x + 2 y 4 = log 2 x - log 2 y
B. log 2 x + 2 y = 2 + 1 2 log 2 x + log 2 y
C. log 2 x + 2 y = log 2 x + log 2 y + 1
D. 4 log 2 x + 2 y = log 2 x + log 2 y
4. Tìm giá trị lớn nhất của các biểu thức a. A = 5 – 8x – x2 b. B = 5 – x2 + 2x – 4y2 – 4y 5. a. Cho a2 + b2 + c2 = ab + bc + ca chứng minh rằng a = b = c b. Tìm a, b, c biết a2 – 2a + b2 + 4b + 4c2 – 4c + 6 = 0 6. Chứng minh rằng: a. x2 + xy + y2 + 1 > 0 với mọi x, y b. x2 + 4y2 + z2 – 2x – 6z + 8y + 15 > 0 Với mọi x, y, z 7. Chứng minh rằng: x2 + 5y2 + 2x – 4xy – 10y + 14 > 0 với mọi x, y.
tìm x;y
a) 4x2+13y+12xy−18y−4x+104x2+13y+12xy−18y−4x+10
b) 4x2+12xy+9y2+4y2−18y−4x+104x2+12xy+9y2+4y2−18y−4x+10
c) (2x+3y)2−2(2x+3y)+1+4y2−12y+9(2x+3y)2−2(2x+3y)+1+4y2−12y+9
d) (2x+3y−1)+(2y−3)2=0
Biểu thức nào dưới đây là bình phương của hiệu x - 2y:
A. x2 + 2xy + 4y2.
B. x2 – 2xy + 4y2 .
C. x2 – 4xy + 4y2 .
D. x2 + 4xy + 4y2
6. Chứng minh rằng:
a. x2 + xy + y2 + 1 > 0 với mọi x, y
b. x2 + 4y2 + z2 - 2x - 6z + 8y + 15 > 0 Với mọi x, y, z
(ai lm giúp với ạ iem cảm ơn nhìu
a) \(x^2+xy+y^2+1\)
\(=x^2+xy+\dfrac{y^2}{4}-\dfrac{y^2}{4}+y^2+1\)
\(=\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1\)
mà \(\left\{{}\begin{matrix}\left(x+\dfrac{y}{2}\right)^2\ge0,\forall x;y\\\dfrac{3y^2}{4}\ge0,\forall x;y\end{matrix}\right.\)
\(\Rightarrow\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1>0,\forall x;y\)
\(\Rightarrow dpcm\)
Đúng 2
Bình luận (0)
b) \(...=x^2-2x+1+4\left(y^2+2y+1\right)+z^2-6z+9+1\)
\(=\left(x-1\right)^2+4\left(y^{ }+1\right)^2+\left(z-3\right)^2+1>0,\forall x.y\)
\(\Rightarrow dpcm\)
Đúng 1
Bình luận (0)
b.
$x^2+4y^2+z^2-2x-6z+8y+15=(x^2-2x+1)+(4y^2+8y+4)+(z^2-6z+9)+1$
$=(x-1)^2+(2y+2)^2+(z-3)^2+1\geq 0+0+0+1>0$ với mọi $x,y,z$
Ta có đpcm.
Đúng 1
Bình luận (0)
Bài 1: Viết biểu thức sau dưới dạng tổng hoặc hiệu 2 bình phương
a) 9x2 + 25 - 12xy + 5y2 - 10y
b) 13x2 + 4x + 12xy + 4y2 + 1
c) x2 + 20 + 9y2 + 8x - 12
a/ x3y2 - xy2 b/ 2x3y2 + 4x2y2 + 2xy2
c/ 3x3y - 12x2y + 12xy d/ 6x3y + 12x2y2 + 6xy3
e/ x2(x – y) + y2(y – x) f/ 9x2(x – 2 ) – 4y2(x - 2)
Giúp mình với đang cần gấp
\(a,x^3y^2-xy^2=xy^2\left(x^2-1\right)=xy^2\left(x-1\right)\left(x+1\right)\\ b,2x^3y^2+4x^2y^2+2xy^2=2xy^2\left(x^2+2x+1\right)=2xy^2\left(x+1\right)^2\\ c,3x^3y-12x^2y+12xy=2xy\left(x^2-4x+4\right)=2xy\left(x-2\right)^2\\ d,6x^3y+12x^2y^2+6xy^3=6xy\left(x^2+2xy+y^2\right)=6xy\left(x+y\right)^2\\ e,x^2\left(x-y\right)+y^2\left(y-x\right)=\left(x^2-y^2\right)\left(x-y\right)=\left(x-y\right)^2\left(x+y\right)\\ f,9x^2\left(x-2\right)-4y^2\left(x-2\right)=\left(9x^2-4y^2\right)\left(x-2\right)=\left(3x-2y\right)\left(3x+2y\right)\left(x-2\right)\)
Tick plz
Đúng 2
Bình luận (0)
a: \(x^3y^2-xy^2=xy^2\left(x^2-1\right)=xy^2\left(x-1\right)\left(x+1\right)\)
b: \(2x^3y^2+4x^2y^2+2xy^2=2xy^2\left(x^2+2x+1\right)=2xy^2\cdot\left(x+1\right)^2\)
c: \(3x^3y-12x^2y+12xy=3xy\left(x^2-4x+4\right)=3xy\cdot\left(x-2\right)^2\)
d: \(6x^3y+12x^2y^2+6xy^3=6xy\left(x^2+2xy+y^2\right)=6xy\cdot\left(x+y\right)^2\)
e: \(x^2\left(x-y\right)+y^2\left(y-x\right)=\left(x-y\right)^2\cdot\left(x+y\right)\)
f: \(9x^2\left(x-2\right)-4y^2\left(x-2\right)=\left(x-2\right)\left(3x-2y\right)\left(3x+2y\right)\)
Đúng 0
Bình luận (0)
11,18y2 - 12xy + 2x2 12,(x2+x)2 + 3(x2+x) + 213,5x2 - 10xy + 5y2 - 20z2 14,x3 - 9x + 2x2 - 1815,x2 - 2x - 4y2 - 4y16,a2 + 2ab + b2 - 2a - 2b + 117,x3 - x + 3x2 y + 3xy2 + y3 - y 18,x3 + y3 + z3 - 3xyz19,x2 + 4x - 520,2x2 - 6x - 821,x2 - 10xy + 9y222,5xz - 5xy - x2 + 2xy - y223,(x2 + x + 1) ( x2 + x + 2) - 1224,(x+1) (x+2) (x+3) (x+4) - 2425,x3 + 2x2 - 2x - 12
Đọc tiếp
11,18y2 - 12xy + 2x2
12,(x2+x)2 + 3(x2+x) + 2
13,5x2 - 10xy + 5y2 - 20z2
14,x3 - 9x + 2x2 - 18
15,x2 - 2x - 4y2 - 4y
16,a2 + 2ab + b2 - 2a - 2b + 1
17,x3 - x + 3x2 y + 3xy2 + y3 - y
18,x3 + y3 + z3 - 3xyz
19,x2 + 4x - 5
20,2x2 - 6x - 8
21,x2 - 10xy + 9y2
22,5xz - 5xy - x2 + 2xy - y2
23,(x2 + x + 1) ( x2 + x + 2) - 12
24,(x+1) (x+2) (x+3) (x+4) - 24
25,x3 + 2x2 - 2x - 12
11: \(2x^2-12xy+18y^2\)
\(=2\left(x^2-6xy+9y^2\right)\)
\(=2\left(x-3y\right)^2\)
12: \(\left(x^2+x\right)^2+3\left(x^2+x\right)+2\)
\(=\left(x^2+x+2\right)\left(x^2+x+1\right)\)
Đúng 1
Bình luận (0)