\(\sqrt{x-2\sqrt{ }x-1}\) Tìm đk để biểu thức xđ
B2
Những câu hỏi liên quan
Tìm đk để các biểu thức sau có nghĩa:
1. \(\sqrt{3x^{2}-x+2}\)
2. \((\dfrac{1}{\sqrt{x}-1}+\dfrac{2}{2-\sqrt{x}}): \dfrac{x}{\sqrt{2x+1}}\)
1: ĐKXĐ: 3x^2-x+2>=0
=>x thuộc R
2: ĐKXĐ: x>=0 và căn x-1<>0 và 2-căn x<>0 và 2x+1>0 và x<>0
=>x>0 và x<>1 và x<>4
Đúng 0
Bình luận (0)
Cho biểu thức
P=\(\dfrac{2\sqrt{x}}{\sqrt{x}+m}+\dfrac{\sqrt{x}}{\sqrt{x}-m}-\dfrac{m^2}{4x-4m^2}\)
a) Rút gọn
b) Tính x theo m để P=0
c) Xđ các g.trị của m để x tìm đc ở câu b t/m đk x>1
a) điều kiện : \(x\ge0;x\ne m^2\)
ta có : \(P=\dfrac{2\sqrt{x}}{\sqrt{x}+m}+\dfrac{\sqrt{x}}{\sqrt{x}-m}-\dfrac{m^2}{4x-4m^2}\)
\(\Leftrightarrow P=\dfrac{2\sqrt{x}}{\sqrt{x}+m}+\dfrac{\sqrt{x}}{\sqrt{x}-m}-\dfrac{m^2}{4\left(\sqrt{x}+m\right)\left(\sqrt{x}-m\right)}\) \(\Leftrightarrow P=\dfrac{2\sqrt{x}\left(\sqrt{x}-m\right)+\sqrt{x}\left(\sqrt{x}+m\right)-m^2}{4\left(\sqrt{x}+m\right)\left(\sqrt{x}-m\right)}\) \(\Leftrightarrow P=\dfrac{3x-\sqrt{x}m-m^2}{4\left(\sqrt{x}+m\right)\left(\sqrt{x}-m\right)}\)b) ta có : \(P=0\Leftrightarrow3x-m\sqrt{x}-m^2\)
ta có : \(\Delta=\left(m^2\right)-3.4\left(-m^2\right)=13m^2\ge0\)
th1: \(m=0\) \(\Rightarrow\) phương trình có nghiệm duy nhất : \(\sqrt{x}=\dfrac{m}{6}\Leftrightarrow x=\dfrac{m^2}{36}\)
th2: \(m\ne0\) \(\Rightarrow\) phương trình có 2 nghiệm phân biệt : \(\left\{{}\begin{matrix}\sqrt{x}=\dfrac{m+\sqrt{13m^2}}{6}\\\sqrt{x}=\dfrac{m-\sqrt{13m^2}}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{14m^2+2\sqrt{13}m^2}{36}\\x=\dfrac{14m^2-2\sqrt{13}m^2}{36}\end{matrix}\right.\)
c) để \(x>1\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2>36\\14m^2+2\sqrt{13}m^2>36\\14m^2-2\sqrt{13}m^2>36\end{matrix}\right.\)
\(\Rightarrow m^2>36\Leftrightarrow\left[{}\begin{matrix}m>6\\m< -6\end{matrix}\right.\)
Đúng 0
Bình luận (2)
mk sữa lại nha .
a) điều kiện : \(x\ge0;x\ne m^2\)
ta có : \(P=\dfrac{2\sqrt{x}}{\sqrt{x}+m}+\dfrac{\sqrt{x}}{\sqrt{x}-m}-\dfrac{m^2}{4x-4m^2}\)
\(\Leftrightarrow P=\dfrac{2\sqrt{x}}{\sqrt{x}+m}+\dfrac{\sqrt{x}}{\sqrt{x}-m}-\dfrac{m^2}{4\left(\sqrt{x}+m\right)\left(\sqrt{x}-m\right)}\) \(\Leftrightarrow P=\dfrac{8\sqrt{x}\left(\sqrt{x}-m\right)+4\sqrt{x}\left(\sqrt{x}+m\right)-m^2}{4\left(\sqrt{x}+m\right)\left(\sqrt{x}-m\right)}\) \(\Leftrightarrow P=\dfrac{12x-4\sqrt{x}m-m^2}{4\left(\sqrt{x}+m\right)\left(\sqrt{x}-m\right)}\)b) ta có : \(P=0\Leftrightarrow12x-4m\sqrt{x}-m^2\)
ta có : \(\Delta'=\left(2m\right)^2-12\left(-m^2\right)=16m^2\ge0\)
th1: \(m=0\) \(\Rightarrow\) phương trình có nghiệm duy nhất : \(\sqrt{x}=\dfrac{2m}{12}=0\Leftrightarrow x=0\)
th2: \(m\ne0\) \(\Rightarrow\) phương trình có 2 nghiệm phân biệt : \(\left\{{}\begin{matrix}\sqrt{x}=\dfrac{2m+\sqrt{16m^2}}{12}\\\sqrt{x}=\dfrac{2m-\sqrt{16m^2}}{12}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{6m}{36}=\dfrac{m}{6}\\x=\dfrac{-2m}{36}=-\dfrac{m}{18}\end{matrix}\right.\)
c) để \(x>1\) \(\Leftrightarrow\left\{{}\begin{matrix}6m>36\\-2m>36\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>6\\m< -18\end{matrix}\right.\Rightarrow m\in\varnothing\)
vậy không có giá trị của \(m\)
Đúng 0
Bình luận (0)
Cho biểu thức Aleft(frac{xsqrt{x}-1}{x-sqrt{x}}-frac{xsqrt{x}+1}{x+sqrt{x}}right):left(1-frac{3-sqrt{x}}{sqrt{x}+1}right)
1) Tìm ĐK XĐ của biểu thức A.
2) Rút gọn A.
3) Tính giá trị của biểu thức A khi frac{1}{6-2sqrt{5}}
4) So sánh A với 1
5) 5) Tìm giá trị của x để giá trị biểu thức A bằng -3.
4) Tìm giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
6) Tìm giá trị của x để giá trị biểu thức A nhỏ hơn -1.
7)Tìm giá trị của x để A 2
Đọc tiếp
Cho biểu thức A=\(\left(\frac{x\sqrt{x}-1}{x-\sqrt{x}}-\frac{x\sqrt{x}+1}{x+\sqrt{x}}\right):\left(1-\frac{3-\sqrt{x}}{\sqrt{x}+1}\right)\)
1) Tìm ĐK XĐ của biểu thức A.
2) Rút gọn A.
3) Tính giá trị của biểu thức A khi \(\frac{1}{6-2\sqrt{5}}\)
4) So sánh A với 1
5) 5) Tìm giá trị của x để giá trị biểu thức A bằng -3.
4) Tìm giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
6) Tìm giá trị của x để giá trị biểu thức A nhỏ hơn -1.
7)Tìm giá trị của x để A < 2
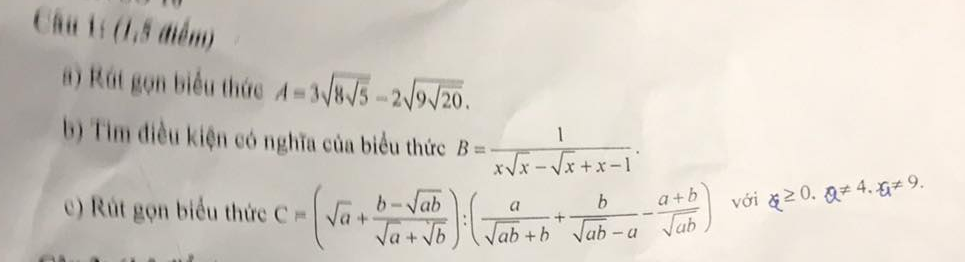
c1
a. rút gọn biểu thức
\(A=3\sqrt{8\sqrt{5}}-2\sqrt{9\sqrt{20}}\)
b. tìm đk có nghĩa của biểu thức
\(B=\dfrac{1}{x\sqrt{x}-\sqrt{x}+x-1}\)
`#Hưng`
\(a,3\sqrt{8\sqrt{5}}-2\sqrt{9\sqrt{20}}\\ =\sqrt{9.8\sqrt{5}}-\sqrt{4.9\sqrt{20}}\\ =\sqrt{72\sqrt{5}}-\sqrt{36\sqrt{20}}\\ =\sqrt{\sqrt{5184.5}}-\sqrt{\sqrt{1296.20}}\\ =\sqrt{\sqrt{25920}}-\sqrt{\sqrt{25920}}\\ =0\)
\(b,ĐKXĐ:x\sqrt{x}-\sqrt{x}+x-1\ne0\\ \Rightarrow\sqrt{x}\left(x-1\right)+\left(x-1\right)\ne0\\ \Rightarrow\left(x-1\right)\left(\sqrt{x}+1\right)\ne0\\ \Rightarrow x-1\ne0\left(vì.\sqrt{x}+1>0\right)\\ \Rightarrow x\ne1\)
Đúng 1
Bình luận (1)
Tìm đk tham số của m để tập xđ hàm số \(f\left(x\right)=\sqrt{x-m}+\sqrt{10-x}\) là một đoạn trên trục số
Hàm số xác định khi:
\(\left\{{}\begin{matrix}x-m\ge0\\10-x\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge m\\x\le10\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi \(m< 10\)
Đúng 0
Bình luận (0)
cho biểu thức A= (\(\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}.\dfrac{\sqrt{x}-2}{\sqrt{x}}\))
a. tìm đk xác định và rút gọn A
b. tìm tất cả giá trị của x để A>\(\dfrac{1}{2}\)
c. tìm tất cả các giá trị để B=\(\dfrac{7}{3}A\),đạt giá trị nguyên
d. tìm tất cả các giá trị để A nhỏ nhất.
CHO BIỂU THỨC:
A=\(\left(\frac{3+\sqrt{x}}{x+\sqrt{x}+1}-\frac{\sqrt{x}-3}{x\sqrt{x}+1}\right).\frac{x^2+x\sqrt{x}-\sqrt{x}-1}{\sqrt{x}}\)
a, tìm điều kiện đối với biến x để A xđ
b, rút gọn
1/ cho biểu thức A =\(\dfrac{x-3}{\sqrt{x-1}-\sqrt{2}}\)
a.tìm đk để A xác định
b. rút gọn A
c. tính giá trị để A= 4(2-\(\sqrt{3}\))
d. tìm tất cả các giá trị để A nhỏ nhất.
\(a,ĐK:x\ne3;x\ge1\\ b,A=\dfrac{\left(\sqrt{x-1}+\sqrt{2}\right)\left(\sqrt{x-1}-\sqrt{2}\right)}{\sqrt{x-1}-\sqrt{2}}=\sqrt{x-1}+\sqrt{2}\\ b,A=4\left(2-\sqrt{3}\right)\\ \Leftrightarrow\sqrt{x-1}+\sqrt{2}=8-4\sqrt{3}\\ \Leftrightarrow\sqrt{x-1}=8-4\sqrt{3}-\sqrt{2}\\ \Leftrightarrow x-1=\left(8-4\sqrt{3}-\sqrt{2}\right)^2\\ \Leftrightarrow x=\left(8-4\sqrt{3}-\sqrt{2}\right)^2+1=...\\ d,A=\sqrt{x-1}+\sqrt{2}\ge\sqrt{2}\\ A_{min}=\sqrt{2}\Leftrightarrow x-1=0\Leftrightarrow x=1\)
Đúng 0
Bình luận (1)
Tìm ĐK để căn thức xác định:
a) \(\sqrt{x-9}+\sqrt{6-x}\)
b) \(\sqrt{\dfrac{-1}{x^2}}\)
a. không có ĐK, vì muốn a đc xác định cần \(\sqrt{x-9}\) và \(\sqrt{6-x}\) \(\ge0\)
mà điều kiện để \(\sqrt{x-9}\) và \(\sqrt{6-x}\ge0\) là \(9\le x\le6\)
Dễ thấy không có số nào tương thích với x
Đúng 1
Bình luận (0)





