39.Tìm m để phương trình y=(3sinx-4cosx)\(^2\)-6sinx+8cosx\(\ge\)2m-1 đúng với x\(\in\)R
DT
Những câu hỏi liên quan
Tìm m để các bất phương trình sau đúng với mọi x: (3sinx – 4cosx)2 – 6sinx + 8cosx ≥ 2m - 1 A. m 1 B. m 1 C. m 2 D. m ≤ 0
Đọc tiếp
Tìm m để các bất phương trình sau đúng với mọi x:
(3sinx – 4cosx)2 – 6sinx + 8cosx ≥ 2m - 1
A. m = 1
B. m > 1
C. m > 2
D. m ≤ 0
Đáp án D
Đặt t = 3sin x - 4cos x => -5 ≤ t ≤ 5 (dùng bất đẳng thức bunhiacopxki)
Ta có: y = (3sin x – 4cos x)2 – 6sin x + 8cos x
= t2 – 2t = (t – 2)2 -1
Do -5 ≤ t ≤ 5 => 0 ≤ (t – 2)2 ≤ 36 => min y = -1
Suy ra yêu cầu bài toán -1 ≥ 2m - 1 ⇔ m ≤ 0.
Đúng 0
Bình luận (0)
Tìm m để các bất phương trình
(
3
sin
x
-
4
cos
x
)
2
-
6
sin
x
+
8
cos
x
≥
2
m
-
1
đúng với mọi
x
∈
ℝ
A. m 0 B.
m
≤
0...
Đọc tiếp
Tìm m để các bất phương trình ( 3 sin x - 4 cos x ) 2 - 6 sin x + 8 cos x ≥ 2 m - 1 đúng với mọi x ∈ ℝ
A. m> 0
B. m ≤ 0
C. m < 0
D. m ≤ 1
Xét hàm số y= ( 3sinx – 4cosx )2 – 6sinx + 8cosx
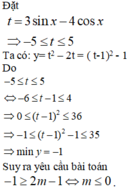
Đáp án B
Đúng 0
Bình luận (0)
tìm m để bất pt \(\left(3sinx-4cosx\right)^2-6sinx+8cosx\ge2m-1\) có nghiệm đúng với mọi x thuộc R
đặt \(3sinx-4cosx=t\) đk \(-5\le t\le5\) pt trên trở thành \(t^2-2t\ge2m-1\)
\(\left(t-1\right)^2\ge2m\Leftrightarrow m\le0\)
Đúng 0
Bình luận (2)
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\sqrt{8cosx-6sinx-\left(3sinx-4cosx\right)^2-2m}\) có tập xác định là R
Hàm xác định trên R khi và chỉ khi:
\(8cosx-6sinx-\left(3sinx-4cosx\right)^2-2m\ge0;\forall x\) (1)
Đặt \(3sinx-4cosx=t\)
\(\Rightarrow t^2=\left(3sinx-4cosx\right)^2\le\left(3^2+\left(-4\right)^2\right)\left(sin^2x+cos^2x\right)=25\)
\(\Rightarrow-5\le t\le5\)
(1) tương đương:
\(-2t-t^2-2m\ge0;\forall t\in\left[-5;5\right]\)
\(\Leftrightarrow2m\le-t^2-2t;\forall t\in\left[-5;5\right]\)
\(\Leftrightarrow2m\le\min\limits_{t\in\left[-5;5\right]}\left(-t^2-2t\right)\)
Xét hàm \(f\left(t\right)=-t^2-2t\) trên \(\left[-5;5\right]\)
\(-\dfrac{b}{2a}=-1\) ; \(f\left(-5\right)=-15\) ; \(f\left(-1\right)=1\) ; \(f\left(5\right)=-35\)
\(\Rightarrow2m\le-35\Rightarrow m\le-\dfrac{35}{2}\)
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để hàm số sau chỉ nhận giá trị dương : y (3sinx - 4cosx)2 - 6sinx + 8cosx + 2m - 1 A. m 1 B. m 1 C. m 2 D. m 1
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số sau chỉ nhận giá trị dương :
y = (3sinx - 4cosx)2 - 6sinx + 8cosx + 2m - 1
A. m = 1
B. m > 1
C. m > 2
D. m < 1
Đáp án B
Đặt t = 3sin x - 4 cos x => -5 ≤ t ≤ 5
Ta có: y = t2 – 2t + 2m – 1 = (t – 1)2 + 2m - 2
Với mọi t ta có (t – 1)2 ≥ 0 nên y ≥ 2m - 2 => min y = 2m - 2
Hàm số chỉ nhận giá trị dương ⇔ y > 0 ∀x ∈ R ⇔ min y > 0
⇔ 2m - 2 > 0 ⇔ m > 1

Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số \(m\le2019\) để bất phương trình : \(\left(3sinx-4cosx\right)^2-6sinx+8cosx\le2m-1\) đúng với mọi \(x\in R\)
A. 2012
B. 2014
C. 2018
D. 2016
Trình bày bài làm chi tiết rồi mới chọn đáp án nha các bạn .
\(\Leftrightarrow\left(3sinx-4cosx\right)^2-2\left(3sinx-4cosx\right)\le2m-1\)
Đặt \(3sinx-4cosx=5\left(\frac{3}{5}sinx-\frac{4}{5}cosx\right)=5sin\left(x-a\right)=t\)
\(\Rightarrow-5\le t\le5\)
BPT trở thành: \(t^2-2t+1\le2m\)
\(\Leftrightarrow\left(t-1\right)^2\le2m\)
Để pt nghiệm đúng với mọi x thì \(2m\ge\max\limits_{\left[-5;5\right]}\left(t-1\right)^2\)
Mà \(\left(t-1\right)^2\le\left(-5-1\right)^2=36\)
\(\Rightarrow2m\ge36\Rightarrow m\ge18\)
Có \(2019-18+1=2002\) giá trị
Không đáp án nào đúng
Tìm điều kiện của m để phương trình
3
sin
x
+
4
cos
x
m
có nghiệm.
Đọc tiếp
Tìm điều kiện của m để phương trình 3 sin x + 4 cos x = m có nghiệm.
![]()
![]()
![]()
![]()
Hình bên là đồ thị của hàm số
y
x
3
-
3
x
Sử dụng đồ thị đã cho, tìm tát cả các giá trị thực của tham số m để bất phương trình
8
sin
3
-
6
sin...
Đọc tiếp
Hình bên là đồ thị của hàm số y = x 3 - 3 x Sử dụng đồ thị đã cho, tìm tát cả các giá trị thực của tham số m để bất phương trình 8 sin 3 - 6 sin x ≤ m nghiệm đúng với mọi x thuộc R
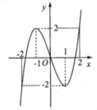
A.![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án A
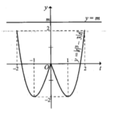
Đặt ![]()
Yều cẩu bào toán trở thành: Tìm m để bất phương trình ![]() nghiệm đúng với mọi
nghiệm đúng với mọi ![]()
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kết quả thỏa mãn yêu cầu bài toán là ![]()
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đồ thị như hình bên dưới.Có bao nhiêu giá trị nguyên của tham số m để phương trình f(3sinx + 4cosx) f(m) có nghiệm? A. 10 B. 14. C. 9 D. 11.
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình bên dưới.
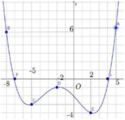
Có bao nhiêu giá trị nguyên của tham số m để phương trình f(3sinx + 4cosx) = f(m) có nghiệm?
A. 10
B. 14.
C. 9
D. 11.



