Xét sự biến thiên và vẽ đồ thị của các hàm số sau:
a.y= x2 - 2x
b.y= -\(\frac{1}{2}\) x2 +2x -2
Xét sự biến thiên của hàm số
\(a.y=-2x^2+x+1\\ b.y=\sqrt{2-x}\\ c.y=\sqrt{2x-x^2}\)
a. Với $x_1, x_2\in\mathbb{R}$ thỏa $x_1\neq x_2$ thì:
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{-2(x_1^2-x_2^2)+(x_1-x_2)}{x_1-x_2}=1-2(x_1+x_2)\)
Với $x_1,x_2> \frac{1}{4}$ thì $A< 0$ nên hàm số nghịch biến trên $(\frac{1}{4}; +\infty)$
Với $x_1,x_2< \frac{1}{4}$ thì $A>0$ nên hàm số đồng biến trên $(-\infty; \frac{1}{4})$
b. TXĐ: $D=(-\infty; 2]$
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{\sqrt{2-x_1}-\sqrt{2-x_2}}{x_1-x_2}=\frac{-1}{\sqrt{2-x_1}+\sqrt{2-x_2}}< 0\)
Vậy hàm số nghịch biến trên tập xác định $(-\infty;2]$
c. TXĐ: $D=[0;2]$
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{\sqrt{2x_1-x_1^2}-\sqrt{2x_2-x_2^2}}{x_1-x_2}=\frac{2-(x_1+x_2)}{\sqrt{2x_1-x_1^2}+\sqrt{2x_2-x_2^2}}\)
Nếu $x_1,x_2\in (1;2)$ thì $A<0$ nên hàm số nghịch biến trên $(1;2)$
Nếu $x_1,x_2\in (0;1)$ thì $A>0$ nên hàm số nghịch biến trên $(0;1)$
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = x2 - 2x - 1
Hàm số y = x2 – 2x – 1 có a = 1 > 0 ; b = –2 ; c = –1:
+ Tập xác định D = R.
+ Nghịch biến trên (–∞ ; 1) ; đồng biến trên (1 ; + ∞).
Bảng biến thiên:
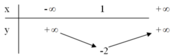
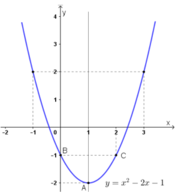
+ Đồ thị hàm số là parabol có:
Đỉnh A(1 ; –2)
Trục đối xứng là đường thẳng x = 1.
Giao điểm với Oy tại B(0 ; –1). Điểm đối xứng với B qua đường thẳng x = 1 là C(2 ; –1).
Đi qua các điểm (3 ; 2) và (–1 ; 2).
đồ thị hàm số y=-2x+1 song song với đồ thị hàm số nào sau đây? A.y=-x+2 B.y=x-2 C.y=2x+1 D.y=-2x+5
Xét sự biến thiên và vẽ đồ thị của các hàm số sau:
a) y=x2-2x
c) y=2x2+6x+3
Xét chiều biến thiên và vẽ đồ thị của các hàm số: y = √x2
Hàm số 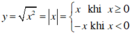 có :
có :
+ Tập xác định D = R.
+ Trên (–∞; 0), hàm số y = –x nghịch biến.
Trên (0 ; +∞), hàm số y = x đồng biến.
Bảng biến thiên :
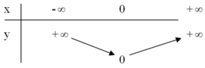
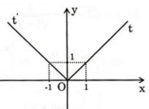
+ Đồ thị hàm số gồm hai phần:
Phần thứ nhất: Nửa đường thẳng y = –x giữ lại phần bên trái trục tung.
Phần thứ hai: Nửa đường thẳng y = x giữ lại phần bên phải trục tung.
Cho hàm số y = 2 x 4 − 4 x 2 (1). Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1).
Tập xác định: D = R
y′=0 ⇔ 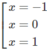
Hàm số đồng biến trên mỗi khoảng (-1; 0) và (1; + ∞ )
Hàm số nghịch biến trên mỗi khoảng (− ∞ ; −1); (0; 1)
Hàm số đạt cực đại tại x = 0; y CĐ = 0
Hàm số đạt cực tiểu tại x = 1 hoặc x = -1; y CT = −2
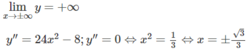
Đồ thị có hai điểm uốn:
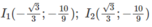
Bảng biến thiên:
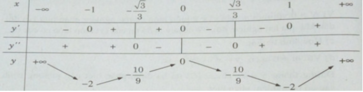
Đồ thị:
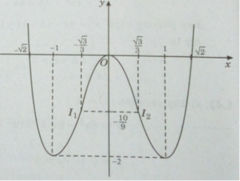
Đồ thị cắt trục hoành tại
Xét chiều biến thiên và vẽ đồ thị của các hàm số: y = 4 - 2x
Hàm số y = 4 – 2x có:
+ Tập xác định D = R
+ Có a = –2 < 0 nên hàm số nghịch biến trên R.
+ Tại x = 0 thì y = 4 ⇒ A(0 ; 4) thuộc đồ thị hàm số.
Tại x = 2 thì y = 0 ⇒ B(2; 0) thuộc đồ thị hàm số.
Vậy đồ thị hàm số là đường thẳng đi qua hai điểm A(0 ; 4) và B(2; 0).
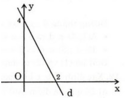
Xét sự biến thiên và vẽ đồ thị của các hàm số sau:
a) y=x2-2x
c) y=2x2+6x+3
Cho P: y=ax2+bx+1. Tìm a,b để:
(P) đi qua B(-1;6) và có tung độ đỉnh là -3.
Bài 2:
Ta có: \(\dfrac{-\text{Δ}}{4a}=-3\)
\(\Leftrightarrow-\text{Δ}=-12a\)
\(\Leftrightarrow b^2-4a=12a\)
\(\Leftrightarrow b^2-16a=0\left(1\right)\)
Thay x=-1 và y=6 vào (P), ta được:
\(a\cdot\left(-1\right)^2+b\left(-1\right)+1=6\)
\(\Leftrightarrow a-b=5\)
\(\Leftrightarrow a=b+5\)(2)
Thay (2) vào (1), ta được:
\(b^2-16\left(b+5\right)=0\)
\(\Leftrightarrow b^2-16b+64-144=0\)
\(\Leftrightarrow\left(b-8\right)^2=144\)
\(\Leftrightarrow\left[{}\begin{matrix}b=20\\b=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=25\\a=1\end{matrix}\right.\)
xét sự biến thiên và vẽ đò thị hàm số sau y=-\( \left| {2x-1} \right|\)