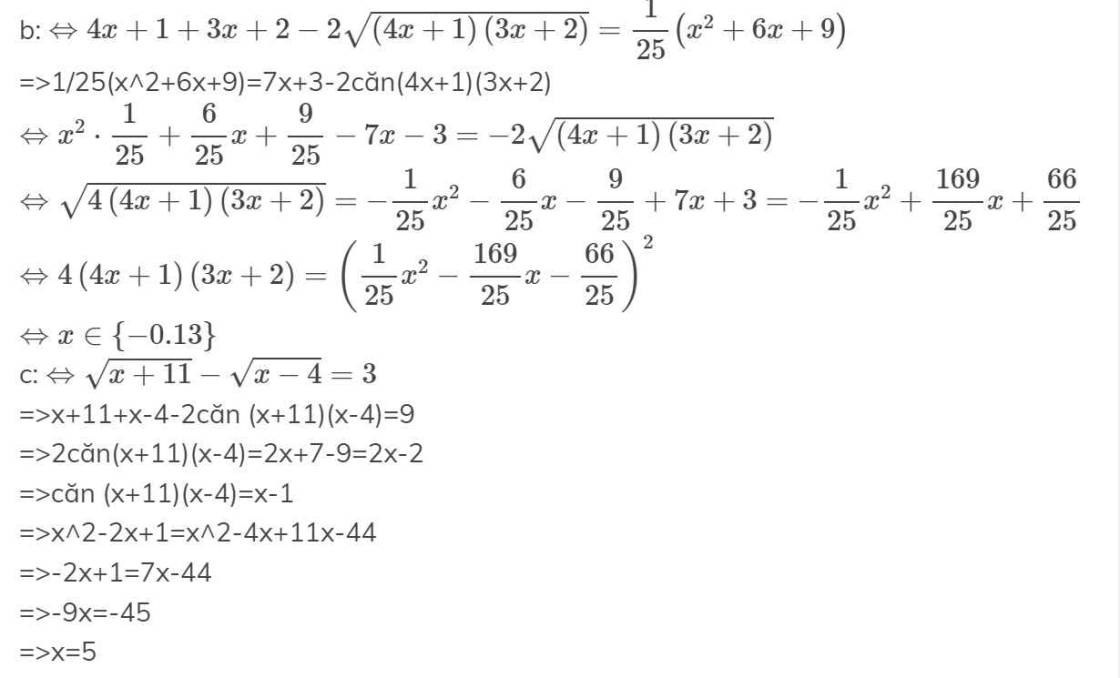\(E=\sqrt{499}vaF=\sqrt{1995}-\sqrt{1994}+...+\sqrt{3}-\sqrt{2}+\sqrt[]{1}\)
VK
Những câu hỏi liên quan
cmr: \(\sqrt{1993\sqrt{1994\sqrt{1995\sqrt{....\sqrt{2501}}}}}<1994\)
tui ko bít làm
mới hok lớp 7 làm được chết liền
Đúng 0
Bình luận (0)
So sánh các số sau: \(\sqrt{1993}+\sqrt{1995}\) và \(2.\sqrt{1994}\)
So sánh các số sau: \(\sqrt{1993}+\sqrt{1995}\) và 2.\(\sqrt{1994}\)
Lời giải:
\((\sqrt{1993}+\sqrt{1995})^2=1993+1995+2.\sqrt{1993.1995}=3988+2\sqrt{(1994-1)(1994+1)}\)
\(=3988+2\sqrt{1994^2-1}< 3988+2\sqrt{1994^2}=3988+2.1994=7976\)
\(\Rightarrow \sqrt{1993}+\sqrt{1995}< \sqrt{7976}\) hay $\sqrt{1993}+\sqrt{1995}< 2\sqrt{1994}$
1.a.Cho biểu thức Mdfrac{left(x-1right).sqrt{3}}{sqrt{x^2-x+1}}.Tính giá trị của biểu thức khi x2+sqrt{3}
b.Cho a,b,c là các số dương và dfrac{a}{b}dfrac{c}{d}.Hãy trục căn thức khỏi mẫu số của biểu thức sau
dfrac{1}{sqrt{a}+sqrt{b}+sqrt{c}+sqrt{d}}
c.Tính tổng Sdfrac{1}{sqrt{1}+sqrt{2}}+dfrac{1}{sqrt{2}+sqrt{3}}+...+dfrac{1}{sqrt{1994}+sqrt{1995}}
Từ đó suy ra rằng Adfrac{1}{sqrt{1}}+dfrac{1}{sqrt{2}}+...+dfrac{1}{sqrt{1994}}86
d.Cho tleft|xright|.sqrt{4-x^2}.Tìm GTLN của t là giá trị tươn...
Đọc tiếp
1.a.Cho biểu thức \(M=\dfrac{\left(x-1\right).\sqrt{3}}{\sqrt{x^2-x+1}}\).Tính giá trị của biểu thức khi \(x=2+\sqrt{3}\)
b.Cho a,b,c là các số dương và \(\dfrac{a}{b}=\dfrac{c}{d}\).Hãy trục căn thức khỏi mẫu số của biểu thức sau
\(\dfrac{1}{\sqrt{a}+\sqrt{b}+\sqrt{c}+\sqrt{d}}\)
c.Tính tổng S=\(\dfrac{1}{\sqrt{1}+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{1994}+\sqrt{1995}}\)
Từ đó suy ra rằng A=\(\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}+...+\dfrac{1}{\sqrt{1994}}>86\)
d.Cho \(t=\left|x\right|.\sqrt{4-x^2}\).Tìm GTLN của t là giá trị tương ứng của x
a: \(=\dfrac{\left(2+\sqrt{3}-1\right)\cdot\sqrt{3}}{\sqrt{7+4\sqrt{3}-2-\sqrt{3}+1}}\)
\(=\dfrac{\left(\sqrt{3}+1\right)\cdot\sqrt{3}}{\sqrt{6+3\sqrt{3}}}=\left(\sqrt{3}+1\right)\cdot\sqrt{\dfrac{1}{2\sqrt{3}+3}}\)
\(=\left(\sqrt{3}+1\right)\cdot\sqrt{\dfrac{\sqrt{3}\left(2-\sqrt{3}\right)}{3}}\)
\(=\left(\sqrt{3}+1\right)\cdot\sqrt{\dfrac{2-\sqrt{3}}{\sqrt{3}}}\)
\(=\sqrt{\dfrac{\left(2-\sqrt{3}\right)\left(4+2\sqrt{3}\right)}{\sqrt{3}}}\)
\(=\sqrt{\dfrac{8-6}{\sqrt{3}}}=\sqrt{\dfrac{2\sqrt{3}}{3}}\)
c: \(=-1+\sqrt{2}-\sqrt{2}+\sqrt{3}+...-\sqrt{1994}+\sqrt{1995}\)
\(=\sqrt{1995}-1\)
Đúng 0
Bình luận (0)
1. Tìm GTLN, GTNN của hàm số: \(y=3\sqrt{x-1}+4\sqrt{5-x}\)
2. Tìm GTLN của biểu thức. \(A=\sqrt{\left(x-1994\right)^2}+\sqrt{\left(x+1995\right)^2}\)
3. Tìm GTNN của biểu thức: \(B=\dfrac{3}{2+\sqrt{2x-x^2+7}}\)
4. Tìm GTNN của: \(C=\dfrac{5-3x}{\sqrt{1-x^2}}\)
Câu 1:
Tìm max:
Áp dụng BĐT Bunhiacopxky ta có:
\(y^2=(3\sqrt{x-1}+4\sqrt{5-x})^2\leq (3^2+4^2)(x-1+5-x)\)
\(\Rightarrow y^2\leq 100\Rightarrow y\leq 10\)
Vậy \(y_{\max}=10\)
Dấu đẳng thức xảy ra khi \(\frac{\sqrt{x-1}}{3}=\frac{\sqrt{5-x}}{4}\Leftrightarrow x=\frac{61}{25}\)
Tìm min:
Ta có bổ đề sau: Với $a,b\geq 0$ thì \(\sqrt{a}+\sqrt{b}\geq \sqrt{a+b}\)
Chứng minh:
\(\sqrt{a}+\sqrt{b}\geq \sqrt{a+b}\)
\(\Leftrightarrow (\sqrt{a}+\sqrt{b})^2\geq a+b\)
\(\Leftrightarrow \sqrt{ab}\geq 0\) (luôn đúng).
Dấu "=" xảy ra khi $ab=0$
--------------------
Áp dụng bổ đề trên vào bài toán ta có:
\(\sqrt{x-1}+\sqrt{5-x}\geq \sqrt{(x-1)+(5-x)}=2\)
\(\sqrt{5-x}\geq 0\)
\(\Rightarrow y=3(\sqrt{x-1}+\sqrt{5-x})+\sqrt{5-x}\geq 3.2+0=6\)
Vậy $y_{\min}=6$
Dấu "=" xảy ra khi \(\left\{\begin{matrix} (x-1)(5-x)=0\\ 5-x=0\end{matrix}\right.\Leftrightarrow x=5\)
Đúng 0
Bình luận (0)
Bài 2:
\(A=\sqrt{(x-1994)^2}+\sqrt{(x+1995)^2}=|x-1994|+|x+1995|\)
Áp dụng BĐT dạng \(|a|+|b|\geq |a+b|\) ta có:
\(A=|x-1994|+|x+1995|=|1994-x|+|x+1995|\geq |1994-x+x+1995|=3989\)
Vậy \(A_{\min}=3989\)
Đẳng thức xảy ra khi \((1994-x)(x+1995)\geq 0\Leftrightarrow -1995\leq x\leq 1994\)
Đúng 0
Bình luận (0)
Bài 3:
Ta thấy:
\(2x-x^2+7=8-(x^2-2x+1)=8-(x-1)^2\leq 8, \forall x\in\mathbb{R}\)
\(\Rightarrow 2+\sqrt{2x-x^2+7}\leq 2+\sqrt{8}=2+2\sqrt{2}\)
\(\Rightarrow B=\frac{3}{2+\sqrt{2x-x^2+7}}\geq \frac{3}{2+2\sqrt{2}}\)
Vậy GTNN của $B$ là \(\frac{3}{2+2\sqrt{2}}\).
Đẳng thức xảy ra tại \((x-1)^2=0\Leftrightarrow x=1\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh
1 + \(\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}\) + ... + \(\dfrac{1}{\sqrt{1994}}\) < \(2\dfrac{1}{\sqrt{1994}}\)
Bài 1 : Cho biểu thức A left(1+frac{sqrt{a}}{a+1}right):left(frac{1}{sqrt{a}-1}-frac{2sqrt{a}}{asqrt{a}+sqrt{a}-a-1}right)a/ Rút gọn Ab/ Tìm a để A 1c/ Tính các giá trị của A nếu a 1995 - 2sqrt{1994}Bài 2 : Cho M frac{3x+sqrt{9x}-3}{x+sqrt{x}-2}-frac{sqrt{x}+1}{sqrt{x}+2}+frac{sqrt{x}-2}{1-sqrt{x}}a/ Rút gọn Mb/ Tim các giá trị của x inZ sao cho MinZ
Đọc tiếp
Bài 1 : Cho biểu thức A = \(\left(1+\frac{\sqrt{a}}{a+1}\right):\left(\frac{1}{\sqrt{a}-1}-\frac{2\sqrt{a}}{a\sqrt{a}+\sqrt{a}-a-1}\right)\)
a/ Rút gọn A
b/ Tìm a để A > 1
c/ Tính các giá trị của A nếu a = 1995 - \(2\sqrt{1994}\)
Bài 2 : Cho M = \(\frac{3x+\sqrt{9x}-3}{x+\sqrt{x}-2}-\frac{\sqrt{x}+1}{\sqrt{x}+2}+\frac{\sqrt{x}-2}{1-\sqrt{x}}\)
a/ Rút gọn M
b/ Tim các giá trị của x \(\in\)Z sao cho M\(\in\)Z
tính \(\frac{1}{\sqrt{6}+\sqrt{5}}+\frac{1}{\sqrt{7}+\sqrt{6}}+\frac{1}{\sqrt{8}+\sqrt{7}}+...+\frac{1}{\sqrt{500}+\sqrt{499}}\)
Giải phương trình
a) \(x^4+\sqrt{x^2+1995}=1995\)
b) \(\sqrt{4x+1}-\sqrt{3x+2}=\dfrac{x+3}{5}\)
c) \(\sqrt{x-4}-\sqrt{x+11}=-3\)