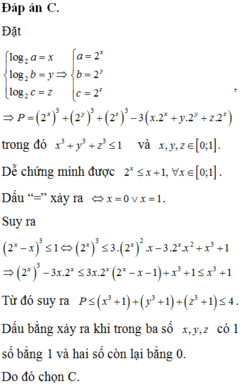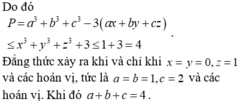Cho a,b,c là các số thuộc đoạn [1;2].Chứng minh rằng:(a+b+c)(1a+1b+1c)≤10
BT
Những câu hỏi liên quan
Cho a,b,c là các số thực thuộc đoạn [0,1 ] .Chứng minh:
\(a\left(b-1\right)+b\left(1-c\right)+c\left(1-a\right)\le1\)
\(a\left(b-1\right)+b\left(1-c\right)+c\left(1-a\right)\le1\\ \Leftrightarrow-abc+ab+bc+ca-a-b-c+1\le2-abc\\ \Leftrightarrow\left(1-a\right)\left(1-b\right)\left(1-c\right)\le2-abc\)
lại có \(abc\le1\) nên \(2-abc\ge1\)
ta chứng minh \(\left(1-a\right)\left(1-b\right)\left(1-c\right)\le1\)
luôn đúng do \(0\le a;b;c\le1\)
vậy bđt dc cm
tick mik nhaaaaa.mik ms l9 thui
Đúng 2
Bình luận (0)
Cho a,b,c là các số thực thuộc đoạn [1,2 ].Chứng minh rằng:
\(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\le10\)
Không mất tính tổng quát, giả sử \(a\ge b\ge c\).
Khi đó: \(\left(a-b\right)\left(b-c\right)\ge0\)
\(\Leftrightarrow ab+bc\ge ac+b^2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{c}+1\ge\dfrac{a}{b}+\dfrac{b}{c}\\\dfrac{c}{a}+1\ge\dfrac{c}{b}+\dfrac{b}{a}\end{matrix}\right.\)
\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}+\dfrac{b}{a}+\dfrac{c}{b}+\dfrac{a}{c}\le2+2\left(\dfrac{a}{c}+\dfrac{c}{a}\right)\)
Vì \(1\le c\le a\le2\Rightarrow\left(\dfrac{a}{c}-2\right)\left(\dfrac{2a}{c}-1\right)\le0\)
\(\Leftrightarrow\dfrac{a}{c}+\dfrac{c}{a}\le\dfrac{5}{2}\)
\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}+\dfrac{b}{a}+\dfrac{c}{b}+\dfrac{a}{c}\le7\)
\(\Leftrightarrow\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\le10\)
Đẳng thức xảy ra khi \(a=b=2;c=1\) và các hoán vị.
Đúng 2
Bình luận (0)
giúp mình với: cho a,b,c là các số thực thuộc đoạn [0;1]. tìm GTLN của biểu thức P=a(1-b)+b(1-c)+c(1-a)
Cho a,b,c là các số thực thuộc đoạn [1;2] thỏa mãn
log
2
3
a
+
log
2
3
b
+
log
2
3
c
≤
1
. Khi biểu thức
P
a
3
+
b
3
+
c
3
-
(...
Đọc tiếp
Cho a,b,c là các số thực thuộc đoạn [1;2] thỏa mãn log 2 3 a + log 2 3 b + log 2 3 c ≤ 1 . Khi biểu thức P = a 3 + b 3 + c 3 - ( log 2 a a + log 2 b b + log 2 c c ) đạt giá trị lớn nhất thì giá trị của tổng a + b + c là:
A. 3
B. 3 . 2 1 3 3
C. 4
D. 6
Cho
a
,
b
,
c
là các số thực thuộc đoạn
1
;
2
thỏa mãn
log
2
3
a
+
log
2
3
b
+
log
2
3
c
≤
1.
Khi biểu thức
P
a...
Đọc tiếp
Cho a , b , c là các số thực thuộc đoạn 1 ; 2 thỏa mãn log 2 3 a + log 2 3 b + log 2 3 c ≤ 1. Khi biểu thức P = a 3 + b 3 + c 3 − 3 log 2 a a + log 2 b b + log 2 c c đạt giá trị lớn nhất thì giá trị của tổng a + b + c là:
A. 2
B. 3.2 1 3 3
C. 4
D. 6
Đáp án C
Nhận xét, với x ∈ 1 ; 2 thì f x = x − log 2 x ≤ 0 . Thật vậy, xét f ' x = x ln 2 − 1 x ln 2
→ f ' x = 0 ⇔ x = 1 ln 2 ⇒ max 1 ; 2 f x = max f 1 , f 1 ln 2 , f 2 = 0
Từ đây suy ra x − 1 ≤ log 2 x ⇒ log 2 3 x ≥ x − 1 3 với 1 ; 2 ⇒ 1 ≥ a − 1 3 + b − 1 3 + c − 1 3
Mặt khác cũng có x 3 − 3 x log 2 x ≤ x 3 − 3 x 1 − x = x 3 − 3 x 2 + 3 x với 1 ; 2
⇒ P − 3 ≤ x − 1 3 + y − 1 3 + z − 1 3 = 1 ⇒ P ≤ 4
Đúng 0
Bình luận (0)
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn . Khi biểu thức đạt giá trị lớn nhất thì giá trị của tổng a+b+c là A. 3 B.
3
.
2
1
3
3
C. 4 D. 6
Đọc tiếp
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn 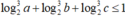 . Khi biểu thức
. Khi biểu thức ![]()
đạt giá trị lớn nhất thì giá trị của tổng a+b+c là
A. 3
B. 3 . 2 1 3 3
C. 4
D. 6
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn
log
2
3
a
+
log
2
3
b
+
log
2
3
c
≤
1
. Khi biểu thức P a3 + b3 + c3 - 3(log2aa + log2bb + log2cc) đạt giá trị lớn nhất thì gi...
Đọc tiếp
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn log 2 3 a + log 2 3 b + log 2 3 c ≤ 1 . Khi biểu thức P = a3 + b3 + c3 - 3(log2aa + log2bb + log2cc) đạt giá trị lớn nhất thì giá trị của tổng a + b + c là:
A. 2
B. 3 . 2 1 3 3
C. 4
D. 6
Đáp án C
Nhận xét, với x ∈ [1;2] thì f(x) = x - log2x ≤ 0. Thật vậy, xét f ' ( x ) = x ln 2 - 1 x ln 2

Từ đây suy ra
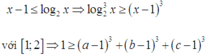
Mặt khác cũng có
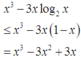
với [1;2]
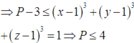
Đúng 0
Bình luận (0)
Cho các số thực a,b,c thuộc đoạn [0;1]. Tìm Max
\(P=\dfrac{a}{b+c+1}+\dfrac{b}{a+c+1}+\dfrac{c}{a+b+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)\)
Không mất tính tổng quát, giả sử \(a\ge b\ge c\)
\(\Rightarrow P\le\dfrac{a}{b+c+1}+\dfrac{b}{b+c+1}+\dfrac{c}{b+c+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)\)
\(\Rightarrow P\le\dfrac{a+b+c}{b+c+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)=\dfrac{a-1}{b+c+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)+1\)
\(\Rightarrow P\le\left(1-a\right)\left[\left(1-b\right)\left(1-c\right)-\dfrac{1}{b+c+1}\right]+1\le\left(1-a\right)\left[\left(1-b\right)\left(1-c\right)-\dfrac{1}{bc+b+c+1}\right]+1\)
\(\Rightarrow P\le\left(1-a\right)\left[\left(1-b\right)\left(1-c\right)-\dfrac{1}{\left(1+b\right)\left(1+c\right)}\right]+1\)
\(\Rightarrow P\le\left(1-a\right)\left(\dfrac{\left(1-b^2\right)\left(1-c^2\right)-1}{\left(1+b\right)\left(1+c\right)}\right)+1\)
Do \(a;b;c\le1\Rightarrow\left\{{}\begin{matrix}1-a\ge0\\\left(1-b^2\right)\left(1-c^2\right)\le1\\\end{matrix}\right.\) \(\Rightarrow\left(1-a\right)\left[\dfrac{\left(1-b^2\right)\left(1-c^2\right)-1}{\left(1+b\right)\left(1+c\right)}\right]\le0\)
\(\Rightarrow P\le1\)
\(P_{max}=1\) khi \(\left(a;b;c\right)=\left(0;0;0\right);\left(1;1;1\right);\left(0;1;1\right);\left(0;0;1\right)\) và các hoán vị
Đúng 2
Bình luận (0)
Cho số phức z=1+i. Gọi S là tập hợp tất cả các điểm biểu diễn số phức w=a+bz+cz2 với a,b,c là các tham số thực thuộc đoạn [0;1]. Tính diện tích hình S?