Vì O là tâm của ngũ giác abcde nên O cũng là trọng tâm của ngũ giác nên vecto oa+ob+oc+od+oe=0

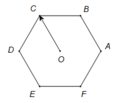
Các vecto cùng phương  O C →  với  có điểm đầu và điểm cuối là các đỉnh của lục giác

: .

Chọn C.

Chọn C.

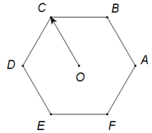
Các vecto cùng phương với  có điểm đầu và điểm cuối là các đỉnh của lục giác : 

Vì ABCDEG là lục giác đều nên:

Các đường chéo chính bằng nhau và cắt nhau tại O, tạo nên các tam giác đều.

Do vậy, các cạnh OA = OB = OC = OD = OE = OG và bằng nửa độ dài đường chéo chính.

\(T=\left|\overrightarrow{DF}\right|=\left|\overrightarrow{DE}+\overrightarrow{EF}\right|\Rightarrow T^2=DE^2+EF^2+\overrightarrow{DE}.\overrightarrow{EF}\)

\(=a^2+a^2+a.a.cos60^0=3a^2\)

\(\Rightarrow\left|\overrightarrow{DF}\right|=a\sqrt{3}\)

\(AC=FD\Rightarrow\left|\overrightarrow{AC}\right|=a\sqrt{3}\)

\(P=\left|\overrightarrow{AI}\right|=\left|\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AC}\right|\Rightarrow P^2=\dfrac{1}{4}\left(AD^2+AC^2+2\overrightarrow{AD}.\overrightarrow{AC}\right)\)

\(=\dfrac{1}{4}\left(4a^2+3a^2+2.2a.a\sqrt{3}.cos30^0\right)=\dfrac{11}{2}a^2\)

\(\Rightarrow\left|\overrightarrow{AI}\right|=\dfrac{a\sqrt{22}}{2}\)

O là trung điểm của của ABCDEG nên KHI VÀ CHỈ KHI các cạnh nối O đều bằng nhau

sorry bạn, mình lớp 7 nên cách trình bày hơi khác