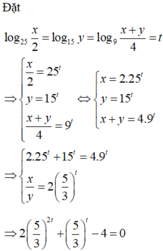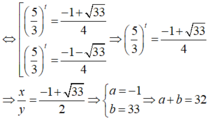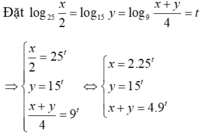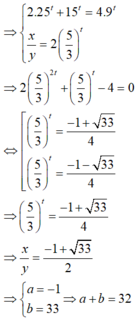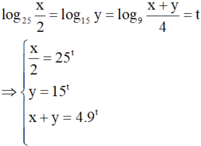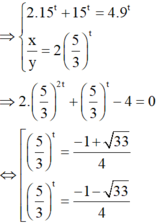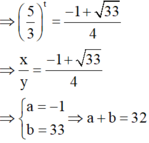Cho các số dương a,b<1 thoả mãn a+b = căn 1-a mũ 2+ caen 1-b mũ 2
KP
Những câu hỏi liên quan
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
9
x
+
y
4
và
x
y
-
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = - a + b 2 với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 32
Đáp án D
Đặt log 25 x 2 = log 15 y = log 9 x + y 4 = t ⇒ x 2 = 25 t y = 15 t x + y = 4 . 9 t
⇒ 2 . 15 t + 15 t = 4 . 9 t x y = 2 5 3 t ⇒ 2 . 5 3 2 t + 5 3 t - 4 = 0 ⇔ [ 5 3 t = - 1 + 33 4 5 3 t = - 1 - 33 4
⇒ 5 3 t = - 1 + 33 4 ⇒ x y = - 1 + 33 4 ⇒ a = - 1 b = 33 ⇒ a + b = 32 .
Đúng 0
Bình luận (0)
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
9
x
+
y
4
và
x
y
−
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = − a + b 2 , với a, b là các số nguyên dương. Tính a+b
A. 14
B. 3
C. 21
D. 32
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
19
x
+
y
4
và
x
y
-
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 19 x + y 4 và x y = - a + b 2 với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 34
Cho các số nguyên dương a,b,c thỏa \(a+b+c=abc\).
Tìm a,b,c nếu a,b,c là các số nguyên dương.
Trả lời
a+b+c=abc (1)
Vì a,b,c có vai trò như nhau
Giả sử \(a\le b\le c\)
\(\Rightarrow a+b+c\le3c\)
\(\Rightarrow a+b\le3\)( nếu \(c\ne0\))
\(\Rightarrow\orbr{\begin{cases}a\ne1;b=2\\a=1;b=3\end{cases}}\)
- Nếu a=1; b=2
=> c=3 (Chọn)
- Nếu a=1; b=3
=>c=2 (loại)
Vậy (a;b;c)\(\in\left\{\left(1;2;3\right);\left(1;3;2\right);\left(2;1;3\right);\left(2;3;1\right);\left(3;1;2\right);\left(3;2;1\right)\right\}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
9
x
+
y
4
và
x
y
-
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = - a + b 2 , với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 32
cho a b c là các số nguyên dương thỏa mãn c + 1/b = a + b/a chứng minh ab là lập phương của 1 số nguyên dương
Gọi \(d=gcd\left(a;b\right)\) khi đó \(a=dm;b=dn\) với \(\left(m;n\right)=1\)
Ta có:
\(c+\frac{1}{b}=a+\frac{b}{a}\Leftrightarrow c=\frac{b}{a}+a-\frac{1}{b}=\frac{dn}{dm}+dm-\frac{1}{dn}\)
\(=\frac{n}{m}+dm-\frac{1}{dn}=\frac{dn^2+d^2m^2n-m}{dmn}\)
Khi đó \(dn^2+d^2m^2n-m⋮dmn\Rightarrow m⋮n\) mà \(\left(m;n\right)=1\Rightarrow n=1\Rightarrow m=d\)
Khi đó \(ab=dm\cdot dn=d^3\) là lập phương số nguyên dương
Tìm số nhỏ nhất trong các số nguyên dương là bội của 2007 và có 4 CS cuối là 2008 (1)
Xét a , b là các số nguyên dương sao cho a + 1 và b + 2007 chia hết cho 6 . CMR : ( 4n + a + b ) chia hết cho 6 (2)
Cho a, b, c là các số nguyên dương thỏa mãn:
a + b + c > 0; ab + bc + ca; abc > 0
Chứng minh rằng cả 3 số đều là các số nguyên dương.
Câu 1: Cho a,b là các số dương thỏa mãn a+b2016. Tìm giá trị lớn nhất của biểu thức Paba.10082 b,2016 c.20162 d.4.20162Câu 2: Cho a,b là các số dương thỏa mãn ab16 và đặt Pdfrac{a+b}{2}. Khẳng định nào sau đây là đúng a.P≥4 b.P≥8 c.dfrac{17}{2} d.5Câu 3: Cho a, b là các số dương. Tìm giá trị nhỏ nhất của biểu thức Pdfrac{a}{b}+dfrac{b}{a}a.2 b.0 c.1 d.-2Câu 4: Tìm mệnh đề đúng a. a2-a+10,∀a ...
Đọc tiếp
Câu 1: Cho a,b là các số dương thỏa mãn a+b=2016. Tìm giá trị lớn nhất của biểu thức P=ab
a.10082 b,2016 c.20162 d.4.20162
Câu 2: Cho a,b là các số dương thỏa mãn ab=16 và đặt P=\(\dfrac{a+b}{2}\). Khẳng định nào sau đây là đúng
a.P≥4 b.P≥8 c.\(\dfrac{17}{2}\) d.5
Câu 3: Cho a, b là các số dương. Tìm giá trị nhỏ nhất của biểu thức P=\(\dfrac{a}{b}+\dfrac{b}{a}\)
a.2 b.0 c.1 d.-2
Câu 4: Tìm mệnh đề đúng
a. a2-a+1>0,∀a b. a2+2a+1>0,∀a c.a2-a≥0, ∀a d.a2-2a-1≥0,∀a
giúp em với ạ
c1:áp dụng bđt AM-GM:
\(a+b\ge2\sqrt{ab}\Rightarrow ab\le\left(\dfrac{a+b}{2}\right)^2=1008^2\)
=> đáp án A
c2: tương tự c1 . đáp án b
Đúng 0
Bình luận (0)
3.
\(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{ab}{ab}}=2\)
Đáp án A
4.
\(a^2-a+1=\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) ;\(\forall a\)
Đáp án A
Đúng 0
Bình luận (0)
- Tích đúng hoặc sai vào các câu sau:
1.Tập hợp số nguyên bao gồm các số nguyên âm và các số nguyên dương
2.Tổng của hai số nguyên âm là một số nguyên dương
3.Tích của ba số nguyên âm và hai số nguyên dương là 1 số nguyên âm
4.Nếu a < thì /a/ = -a
5.Cho a thuộc N thì (-a) là số nguyên âm
6.Cho a,b thuộc Z,nếu /a/ = /b/ thì a=b
câu 5 đúng các câu còn lại sai bạn nhé
Đúng 0
Bình luận (0)
Xem thêm câu trả lời