a/

\(\Rightarrow3=4m.2-m-5\Leftrightarrow m=\dfrac{8}{5}\)

b/

Tọa độ A là \(A\left(x_0;y_0\right)\)

\(\Rightarrow y_0=4mx_0-m-5\forall m\)

\(\Leftrightarrow\left(4x_0-1\right)m-\left(y_0+5\right)=0\forall m\)

\(\Leftrightarrow\left\{{}\begin{matrix}4x_0-1=0\\y_0+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=\dfrac{1}{4}\\y_0=-5\end{matrix}\right.\)

=> d1 luân đi qua điểm A cố định \(A\left(\dfrac{1}{4};-5\right)\forall m\)

Tọa độ B là \(B\left(x_1;y_1\right)\)

\(\Rightarrow y_1=\left(3m^2+1\right)x_1+m^2-4\forall m\)

\(\Leftrightarrow3m^2x_1+x_1+m^2-4-y_1=0\forall m\)

\(\Leftrightarrow\left(3x_1+1\right)m^2+x_1-y_1-4=0\forall m\)

\(\Leftrightarrow\left\{{}\begin{matrix}3x_1+1=0\\x_1-y_1-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{3}\\y_1=-\dfrac{13}{3}\end{matrix}\right.\)

=> d2 luân đi qua điểm B cố định \(B\left(-\dfrac{1}{3};-\dfrac{13}{3}\right)\)

d/ d1//d2 khi

\(\left\{{}\begin{matrix}4m=3m^2+1\\-m-5\ne m^2-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m_1=1\\m_2=\dfrac{1}{3}\end{matrix}\right.\\m^2+m+1\ne0\end{matrix}\right.\)

Ta có \(m^2+m+1>0\forall m\)

\(\Rightarrow\left[{}\begin{matrix}m_1=1\\m_2=\dfrac{1}{3}\end{matrix}\right.\)

e/

\(\Rightarrow4mx-\left(m+5\right)=\left(3m^2+1\right)x+m^2-4\) tìm m để phương trình có nghiệm

Tìm giao

\(\Rightarrow4mx-\left(m+5\right)=\left(3m^2+1\right)x+m^2-4\) khi m=2

Thay m=2 tìm x rồi thay vào d1 hoặc d2 để tìm y

\(a,\Leftrightarrow\left\{{}\begin{matrix}2-m>0\\m-4>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m>4\end{matrix}\right.\Leftrightarrow m\in\varnothing\\ b,\Leftrightarrow2-m=m-4\Leftrightarrow m=3\\ c,\Leftrightarrow2-m\ne m-4\Leftrightarrow m\ne3\)

2:

a: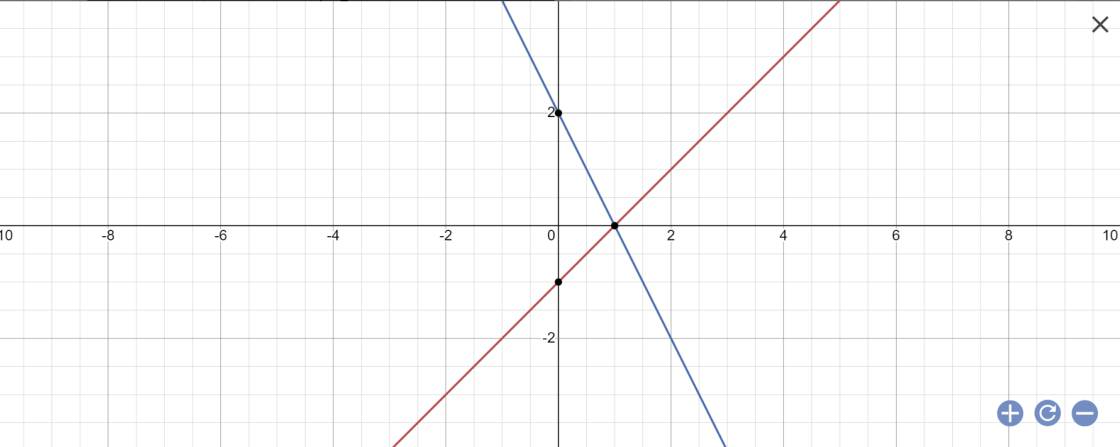 

b: Tọa độ giao điểm là nghiệm của hệ:

x-1=-2x+2 và y=x-1

=>3x=3 và y=x-1

=>x=1 và y=1-1=0

1:

a: Thay x=-1 và y=0 vào (d), ta được:

m+1=0

=>m=-1

c: tọa độ giao điểm là:

2x-2=-x+4 và y=2x-2

=>3x=6 và y=2x-2

=>x=2 và y=4-2=2

Thay x=2 và y=2 vào (d), ta được:

m-2=2

=>m=4

a: Để d1//d2 thì \(\left\{{}\begin{matrix}3m^2+1-4m=0\\-m-5< >m^2-9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(3m-1\right)\left(m-1\right)=0\\m^2-9+m+5< >0\end{matrix}\right.\)

=>m=1/3 hoặc m=1

b: Để hai đường cắt nhau thì (3m-1)(m-1)<>0

hay \(m\notin\left\{\dfrac{1}{3};1\right\}\)

\(\left(d_1\right)\text{//}\left(d_2\right)\Leftrightarrow\left\{{}\begin{matrix}m-3=-2m\\m^2-6\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=1\\m\ne\pm3\end{matrix}\right.\Leftrightarrow m=1\\ \left(d_1\right)\cap\left(d_2\right)\text{ tại 1 điểm trên Oy}\\ \Leftrightarrow\left\{{}\begin{matrix}y=\left(m-3\right)\cdot0+m^2-6\\y=-2m\cdot0+3=3\end{matrix}\right.\Leftrightarrow m^2-6=3\\ \Leftrightarrow\left[{}\begin{matrix}m=3\\m=-3\end{matrix}\right.\\ \left(d_1\right)\equiv\left(d_2\right)\Leftrightarrow\left\{{}\begin{matrix}m-3=-2m\\m^2-6=3\end{matrix}\right.\Leftrightarrow m\in\varnothing\)