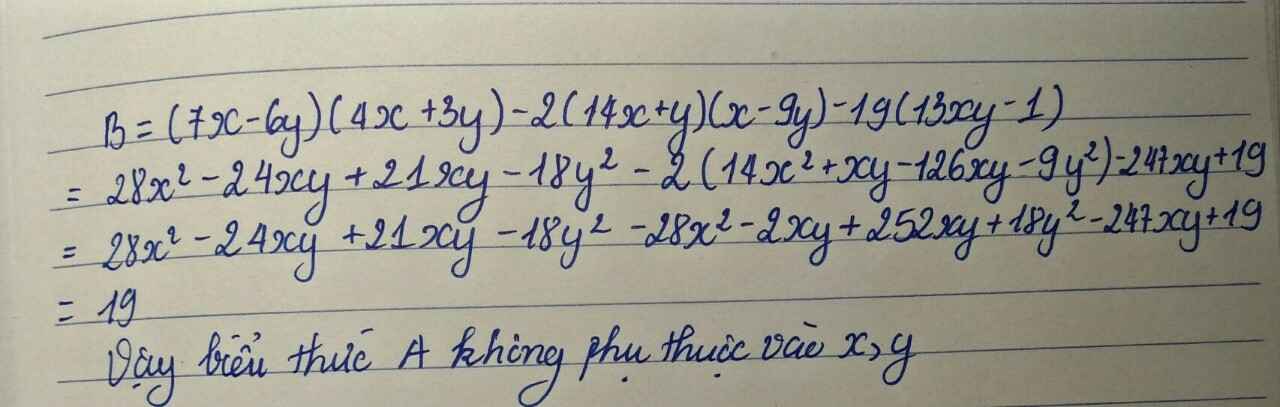B = ( 7x - 6y ) ( 4x + 3y ) - 2 ( 14x + y ) ( x - 9y ) - 19 ( 13xy - 1 )
LG
Những câu hỏi liên quan
Tính giá trị biểu thức:
B = (7x – 6y)(4x + 3y) – 2(14x + y)(x – 9y) – 19(13xy – 1) ?
Em cần gấp ạ.
A= ( 4x - 5)(2x+3) - 4(x+2)(2x - 1)+(10x+7)
B=(7x - 6y)(4x+3y) - 2(14x+y)(x - 9y) - 19(13xy - 1)
Chứng minh rằng giá trị của biểu thức ko phụ thuộc vào giá trị biến :
A) ( 4x - 5 )( 2x + 3 ) - 4( x + 2 )( 2x - 1 ) + ( 10x + 7 )
B) ( 7x - 6y )( 4x + 3y ) - 2 (14x + y )( x - 9y ) - 19(13xy- 1)
nếu ta dùng cách rút gọn biểu thức thì ta có kết quả
A=(8a-8)x2+(2a-2)x-15a+15
còn nếu sử dụng cách Phân tích thành nhân tử thì ta sẽ có kết quả là
A=(a-1)(2x+3)(4x-5)
(tự xét )
B = (7x - 6y)×(4x + 3y) - 2×(14x + y)×(x - 9y) - 19×(13xy - 1)
= 28x^2 - 24xy + 21xy - 18y^2 - 2.(14x^2 + xy - 126xy - 9y^2) - 247xy + 19
= 28x^2 - 24xy + 21xy - 18y^2 - 28x^2 - 2xy + 252xy + 18y^2 - 247xy + 19
= 19
vậy biểu thức A ko phụ thuộc vào x, y
hc tốt
Đúng 0
Bình luận (0)
tớ chỉ biết làm phần B thôi
B= (7x - 6y)×(4x + 3y) - 2×(14x + y)×(x - 9y) - 19×(13xy - 1)
= 28x^2 - 24xy + 21xy - 18y^2 - 2.(14x^2 + xy - 126xy - 9y^2) - 247xy + 19
= 28x^2 - 24xy + 21xy - 18y^2 - 28x^2 - 2xy + 252xy + 18y^2 - 247xy + 19
= 19
vậy biểu thức A ko phụ thuộc vào x, y
phần A tương tự
Đúng 0
Bình luận (0)
Cảm ơn 2 cậu nhìu nha!!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng tỏ các biểu thức sau ko phụ thuộc vào biến
a, x2 * ( 2x +1 ) - x2 ( x + 2 ) + x3 - ( x+3)
b, 4* (x-6) - x2 ( 2+ 3x ) +x*(5x-4) +3x2
c, ( 4x -5 ) * ( 2x+3) -4*(x+2) * ( 2x-1) + 10x+7
d, ( 7x -6y ) * ( 4x +3y) - 2*( 11x +y) * (x-9y) -19 * (13xy-1)
Tìm GTNN của các câu sau đây:
a) A=4x^2+y^2-12x+3y+5
b) B=x^2+9y^2+4x-6y-1
c) C= 25x^2+4y^2-10x-6y+3
d) D=x^2+y^2+z^2-x+2y+3z-1
b: Ta có: \(B=x^2+4x+9y^2-6y-1\)
\(=x^2+4x+4+9y^2-6y+1-6\)
\(=\left(x+2\right)^2+\left(3y-1\right)^2-6\ge-6\forall x,y\)
Dấu '=' xảy ra khi x=-2 và \(y=\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
1) Chứng minh biểu thức sau ko phụ thuộc vào biến x, y
3y(-3-2)²-(3y-1)(9y²+3y+1)-(-6y-1)²
2) tìm x
a: (2x+5)(2x-7)-(-4x-3)²=16
b:(8x²+3)(8x²-3)-(8x²-1)²=22
c:49x²+14x+1=0
d:(x-1)³-x(x-2)²-(x-2)=0
Bài 2:
a: \(\Leftrightarrow4x^2-14x+10x-35-\left(4x+3\right)^2=16\)
\(\Leftrightarrow4x^2-4x-35-16x^2-24x-9-16=0\)
\(\Leftrightarrow-12x^2-28x-60=0\)
\(\Leftrightarrow3x^2+7x+15=0\)
\(\text{Δ}=7^2-4\cdot3\cdot15=-131< 0\)
Do đó: Phương trình vô nghiệm
b: Ta có: \(\left(8x^2+3\right)\left(8x^2-3\right)-\left(8x^2-1\right)^2=22\)
\(\Leftrightarrow64x^4-9-64x^4+16x^2-1=22\)
\(\Leftrightarrow16x^2=32\)
hay \(x\in\left\{\sqrt{2};-\sqrt{2}\right\}\)
c: Ta có: \(49x^2+14x+1=0\)
=>\(\left(7x+1\right)^2=0\)
hay x=-1/7
Đúng 0
Bình luận (0)
Cho x, y thỏa mãn
\(7x^2+9y^2+12xy-4x-6y-15=0\)
Tìm Max; Min của S = 2x+3y+5
1) Chứng minh biểu thức sau ko phụ thuộc vào biến x, y
3y(-3-2)²-(3y-1)(9y²+3y+1)-(-6y-1)²
2) tìm x
a: (2x+5)(2x-7)-(-4x-3)²=16
b:(8x²+3)(8x²-3)-(8x²-1)²=22
c:49x²+14x+1=0
d:(x-1)³-x(x-2)²-(x-2)=0
Giúp mk, mk đang cần gấp
Bài 2:
a: \(\Leftrightarrow4x^2-14x+10x-35-\left(4x+3\right)^2=16\)
\(\Leftrightarrow4x^2-4x-35-16x^2-24x-9-16=0\)
\(\Leftrightarrow-12x^2-28x-60=0\)
\(\Leftrightarrow3x^2+7x+15=0\)
\(\text{Δ}=7^2-4\cdot3\cdot15=-131< 0\)
Do đó: Phương trình vô nghiệm
b: Ta có: \(\left(8x^2+3\right)\left(8x^2-3\right)-\left(8x^2-1\right)^2=22\)
\(\Leftrightarrow64x^4-9-64x^4+16x^2-1=22\)
\(\Leftrightarrow16x^2=32\)
hay \(x\in\left\{\sqrt{2};-\sqrt{2}\right\}\)
c: Ta có: \(49x^2+14x+1=0\)
=>\(\left(7x+1\right)^2=0\)
hay x=-1/7
Đúng 0
Bình luận (0)
tìm x y 1+3y/12=1+6y/5x=1+9y/4x