tìm GTLN của A=\(\dfrac{3}{x-1}+\dfrac{4}{x}\)
PA
Những câu hỏi liên quan
a) Tìm GTNN Của:
A=\(\left(2x+\dfrac{1}{3}\right)^4-1\)
a) Tìm GTLN Của:
B=\(-\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^6+3\)
\(B=-\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^6+3\)
vì \(B=-\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^6\le0,\forall x\inℝ\)
\(\Rightarrow B=-\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^6+3\le3\)
Dấu "=" xảy ra khi và chỉ khi
\(\dfrac{4}{9}x-\dfrac{2}{15}=0\Rightarrow\dfrac{4}{9}x=\dfrac{2}{15}\Rightarrow x=\dfrac{9}{15}\)
Vậy \(GTLN\left(B\right)=3\left(tạix=\dfrac{9}{15}\right)\)
Đúng 1
Bình luận (0)
\(A=\left(2x+\dfrac{1}{3}\right)^4-1\)
vì \(\left(2x+\dfrac{1}{3}\right)^4\ge0,\forall x\inℝ\)
\(\Rightarrow A=\left(2x+\dfrac{1}{3}\right)^4-1\ge-1\)
Dấu "=" xảy ra khi và chỉ khi
\(2x+\dfrac{1}{3}=0\Rightarrow2x=-\dfrac{1}{3}\Rightarrow x=-\dfrac{1}{6}\)
\(\Rightarrow GTNN\left(A\right)=-1\left(tạix=-\dfrac{1}{6}\right)\)
Đúng 2
Bình luận (0)
Cho biểu thức M=\(\dfrac{x^4+2}{x^6+1}+\dfrac{x^2-1}{x^4-x^2+1}-\dfrac{x^2+3}{x^4+4x^2+3}\)
a) Rút gọn M
b) Tìm GTLN của M
`a)M=(x^4+2)/(x^6+1)+(x^2-1)/(x^4-x^2+1)-(x^2+3)/(x^4+4x^2+3)`
`=(x^4+2)/(x^6+1)+(x^2-1)/(x^4-x^2+1)-(x^2+3)/((x^2+1)(x^2+3))`
`=(x^4+2)/(x^6+1)+((x^2-1)(x^2+1))/(x^6+1)-1/(x^2+1)`
`=(x^4+2+x^4-1-x^4+x^2-1)/(x^2+1)`
`=(x^4+x^2)/(x^2+1)`
`=(x^2(x^2+1))/(x^2+1)`
`=x^2`
`b)` tìm gtnn chứ?
`M=x^2>=0`
Dấu '=" `<=>x=0`
Đúng 2
Bình luận (0)
tìm gtln gtnn của:
\(A=\left|x+1\right|-3\)
\(B=-\left|x-\dfrac{3}{7}\right|-\dfrac{1}{4}\)
\(A=\left|x+1\right|-3\\ min_A=-3.khi.x+1=0\Leftrightarrow x=-1\\ B=-\left|x-\dfrac{3}{7}\right|-\dfrac{1}{4}\\ max_B=-\dfrac{1}{4}.khi.\left(x-\dfrac{3}{7}\right)=0\Leftrightarrow x=\dfrac{3}{7}\)
Đúng 0
Bình luận (0)
a)
A = |x + 1| - 3 ≥ 0 - 3 = -3
Dấu "=" xảy ra khi x + 1 = 0 hay x = -1
Do đó A đạt GTNN là -3 khi x = -1
b)
\(B=-\left|x-\dfrac{3}{7}\right|-\dfrac{1}{4}\le-0-\dfrac{1}{4}=-\dfrac{1}{4}\)
Dấu "=" xảy ra khi khi \(x-\dfrac{3}{7}=0\) hay \(x=\dfrac{3}{7}\)
Do đó B đạt GTLN là \(-\dfrac{1}{4}\) khi \(x=\dfrac{3}{7}\)
Đúng 0
Bình luận (0)
\(A=\left(\dfrac{4x}{x+2}-\dfrac{x^3-8}{x^3+8}\times\dfrac{4x^2-8x+16}{x^2-4}\right)\div\dfrac{16}{x+2}\times\dfrac{x^2+3x+2}{x^2+x+1}\)
\(B=\dfrac{x^2+x-2}{x^3-1}\)
a) Tìm ĐKXĐ của A, B. Rút gọn A, B
b)Tìm GTLN của A+B
Tìm GTLN của biểu thức: \(A=\left(\dfrac{x^2}{x^2-3x+2}+\dfrac{x^2}{x^2-5x+6}\right):\dfrac{x^4+x^2+1}{x^2-4x+3}\)
Bạn tham khảo lời giải tại đây:
Tìm GTLN của biểu thức: \(A=\left(\dfrac{x^2}{x^2-3x 2} \dfrac{x^2}{x^2-5x 6}\right):\dfrac{x^4 x^2 1}{x^2-4x 3}\) - Hoc24
Đúng 1
Bình luận (0)
Tìm GTLN của biểu thức: \(A=\left(\dfrac{x^2}{x^2-3x+2}+\dfrac{x^2}{x^2-5x+6}\right):\dfrac{x^4+x^2+1}{x^2-4x+3}\)
Lời giải:
ĐK: $x\neq 1;2;3$
\(A=x^2\left[\frac{1}{(x-1)(x-2)}+\frac{1}{(x-2)(x-3)}\right].\frac{(x-1)(x-3)}{x^4+x^2+1}\)
\(=x^2.\frac{x-3+x-1}{(x-1)(x-2)(x-3)}.\frac{(x-1)(x-3)}{x^4+x^2+1}=x^2.\frac{2(x-2)}{(x-1)(x-2)(x-3)}.\frac{(x-1)(x-3)}{x^4+x^2+1}=\frac{2x^2}{x^4+x^2+1}\)
Áp dụng BĐT AM-GM: $x^4+1\geq 2x^2$
$\Rightarrow A\leq \frac{2x^2}{2x^2+x^2}=\frac{2}{3}$
Vậy $A_{\max}=\frac{2}{3}$. Giá trị đạt tại $x^4=1$ hay $x=-1$ (do $x\neq 1$)
Đúng 2
Bình luận (3)
Cho biểu thức: K=(\(\dfrac{x^2}{x^2-5x+6}\)+\(\dfrac{x^2}{x^2-3x+2}\)).\(\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+x^2+1}\)
a, Tìm đkxđ rồi rút gọn K
b, Tìm GTLN của K
a: ĐKXĐ: x<>1; x<>2; x<>3
\(K=\left(\dfrac{x^2}{\left(x-2\right)\left(x-3\right)}+\dfrac{x^2}{\left(x-1\right)\left(x-2\right)}\right)\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+2x^2+1-x^2}\)
\(=\dfrac{x^3-x^2+x^3-3x^2}{\left(x-2\right)\left(x-3\right)\left(x-1\right)}\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x^2+1+x\right)\left(x^2+1-x\right)}\)
\(=\dfrac{2x^3-4x^2}{\left(x-2\right)}\cdot\dfrac{1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^2\left(x-2\right)}{\left(x-2\right)\left(x^4+x^2+1\right)}=\dfrac{2x^2}{x^4+x^2+1}\)
b:
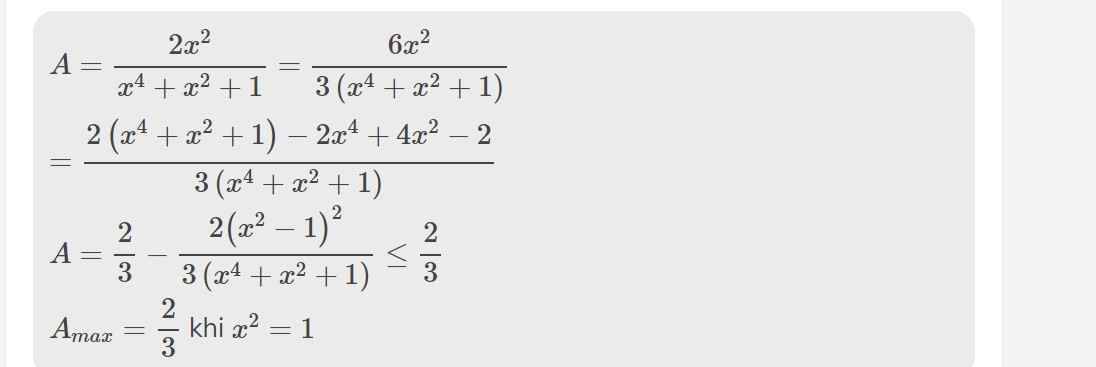
Đúng 0
Bình luận (0)
Bài 4: Cho biểu thức A \(=\left(\dfrac{1}{x+2}-\dfrac{2}{x-2}-\dfrac{x}{4-x^2}\right):\dfrac{6\left(x+2\right)}{\left(2-x\right)\left(x+1\right)}\)
a) Rút gọn A
b)Tìm x để A > 0
c) Tìm x biết x2 + 3x + 2 \(=0\)
d) Tìm x để A đạt GTLN, tìm GTLN đó
a: \(A=\dfrac{x-2-2x-4+x}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-\left(x-2\right)\left(x+1\right)}{6\left(x+2\right)}\)
\(=\dfrac{-6}{\left(x+2\right)}\cdot\dfrac{-\left(x+1\right)}{6\left(x+2\right)}=\dfrac{\left(x+1\right)}{\left(x+2\right)^2}\)
b: A>0
=>x+1>0
=>x>-1
c: x^2+3x+2=0
=>(x+1)(x+2)=0
=>x=-2(loại) hoặc x=-1(loại)
Do đó: Khi x^2+3x+2=0 thì A ko có giá trị
Đúng 0
Bình luận (0)
Tìm GTLN của \(A=\dfrac{\left(x+2\right)^2}{2}\times\left(1-\dfrac{x^2}{x+2}\right)-\dfrac{x^2+6x+4}{x}\)
Bạn coi lại xem có viết nhầm chỗ nào trong biểu thức không? Biểu thức này nội việc rút gọn thôi đã "xấu" rồi.
Đúng 0
Bình luận (0)
1. Tìm GTNN của \(y=x+\dfrac{1}{x}-5\) trên \(\left(0,+\infty\right)\)
2. Tìm GTNN của \(y=4x^2+\dfrac{1}{x}-4\) trên \(\left(0,+\infty\right)\)
3. Tìm GTLN của \(y=\dfrac{x^2+4}{x}\) trên \(\left(-\infty,0\right)\)
\(y=x+\dfrac{1}{x}-5\ge2\sqrt{\dfrac{x}{x}}-5=-3\)
\(y_{min}=-3\) khi \(x=1\)
\(y=4x^2+\dfrac{1}{2x}+\dfrac{1}{2x}-4\ge3\sqrt[3]{\dfrac{4x^2}{2x.2x}}-4=-1\)
\(y_{min}=-1\) khi \(x=\dfrac{1}{2}\)
\(y=x+\dfrac{4}{x}\Rightarrow y'=1-\dfrac{4}{x^2}=0\Rightarrow x=-2\)
\(y\left(-2\right)=-4\Rightarrow\max\limits_{x>0}y=-4\) khi \(x=-2\)
Đúng 0
Bình luận (0)





