Cho tam giác ABC nhọn các đường cao AD và BE cắt nhau tại H. Chứng minh tanB*tanC=\(\frac{AD}{HD}\)
NT
Những câu hỏi liên quan
tam giác ABC có ba góc nhọn, đường cao AD và BE cắt nhau tại H. biết AH /HD=k. chứng minh tanB x tanC = 1+k
Cho tam giác ABC có ba góc nhọn với các đường cao AD, BE, CF cắt nhau tại H. Biết AH=k.HD . Chứng minh rằng: tanB. tanC=k+1
Cho tam giác ABC có ba góc nhọn Vẽ đường cao AD và BE. Gọi H là trực tâm và G là trọng tâm của tam giác ABC. C/m:
a) tanB*tanC= AD/HD
b) HG song song với BC C/m: tanB*tanC=3
Cho tam giác nhọn ABC, hai đường cao AD và BE cắt nhau tại H. Biết HD:HA=1:2. Cmr tanB+tanC=3
giải tiếp mình nhé... Gấp lắm
Mình có nghe nói là 2 nhà toán học Alfred North Whitehead và Bertrand Russell đã chứng minh 1+1=2 trong quyển Principa Mathemaa (tạm dịch: nền tảng của toán học). Họ đã mất hơn 360 trang để chứng minh điều này. Thầy giáo bạn gãi đầu là phải.
Phép chứng minh này dựa trên một bộ 9 tiên đề về tập hợp gọi tắt là ZFC (Zermelo–Fraenkel). Rất nhiều lý thuyết số học hiện đại dựa trên những tiên đề này. Nếu có người chứng minh được một trong những tiên đề đó là sai (VD: 2 tập hợp có cùng các phần tử mà vẫn không bằng nhau) thì rất có thể dẫn đến 1+1 != 2
Đúng 0
Bình luận (0)
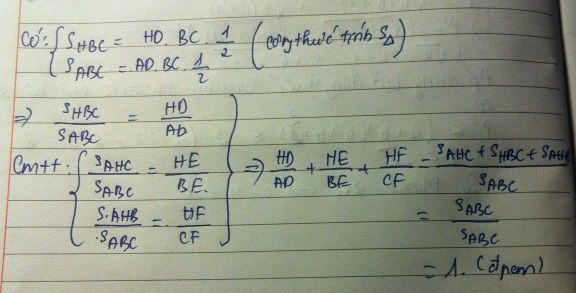
cho tam giác ABC nhọn các đường cao AD, BE, CF cắt nhau tại H chứng minh rằng \(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=1\)
Cho △ABC nhọn, các đường cao AD, BI, CK cắt nhau tại H. DE⊥AB tại E, DF⊥AC tại F.
a. Chứng minh AE*AB=AF*AC.
b. Cho HD=AD/3. Tính tanB*tanC
a: Xét ΔADB vuông tại D có DE là đường cao
nên \(AE\cdot AB=AD^2\left(1\right)\)
Xét ΔADC vuông tại D có DF là đường cao
nên \(AF\cdot AC=AD^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, đường cao AD, BE cắt nhau tại H. Đường trung tuyến AM. G là trọng tâm tam giác ABC. Cho HG song song BC. Chứng minh TanB*TanC=3
cho tam giác abc nhọn có đường cao ad,be,cf cắt nhau tại h. chứng minh tg aef~ tg abc và tanB.tanC=AD/HD
Xét ∆ABE và ∆ACF có:
\(\widehat{A}\left(chung\right)\)
\(\widehat{AEB}=\widehat{AFC}\left(=90^0\right)\)
\(\Rightarrow\)∆ABE ~ ∆ACF (g-g)
\(\Rightarrow\frac{AE}{AF}=\frac{AB}{AC}\Rightarrow\frac{AE}{AB}=\frac{AF}{AC}\)
Xét ∆AEF và ∆ABC có:
\(\frac{AE}{AB}=\frac{AF}{AC}\left(cmt\right)\)
\(\widehat{A}\left(chung\right)\)\
\(\Rightarrow\)∆AEF ~ ∆ABC (đpcm)
Ta có: \(\tan B=\frac{ÁD}{DB};\tan C=\frac{AD}{DC}\)
Xét ∆ADC và ∆BDH có:
\(\widehat{HBD}=\widehat{CAD}\)( cùng phụ với \(\widehat{C}\))
\(\widehat{ADC}=\widehat{BDH}\left(=90^0\right)\)
\(\Rightarrow\)∆ADC ~ ∆ BDH (g-g)
\(\Rightarrow\frac{AD}{DC}=\frac{BD}{DH}\)
\(\Rightarrow\tan B\cdot\tan C=\frac{AD}{DB}\cdot\frac{AD}{DC}=\frac{AD}{DB}\cdot\frac{BD}{DH}=\frac{AD}{DH}\)(đpcm)
Cho tam giác nhọn ABC có đường cao AD, BE, CF cắt nhau tại H. Gọi I là giao điểm của EF và AH. Chứng minh AD*HD=DB*CD
Tam giác AEF đồng dạng tam giác ABC
AI*HD=IH*AD