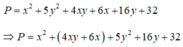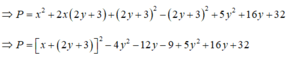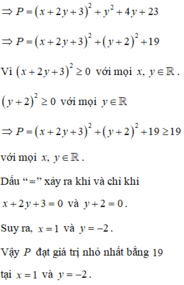Tìm x,y thuộc Z
x2 + 4xy = 6 + 5y2
SD
Những câu hỏi liên quan
Tìm các số nguyên x,y thỏa mãn:
x2 + 5y2 +4xy - 2y < 0
=>x^2+4xy+4y^2+y^2-2y<0
=>y^2-2y<0
=>0<y<2
=>y=1 và \(x\in Z\)
Đúng 0
Bình luận (0)
Cho x, y là hai số thực tùy ý, tìm giá trị nhỏ nhất của biểu thức sau: P = x 2 + 5 y 2 + 4 x y + 6 x + 16 y + 32
Tìm GTNN:
1. G=2x2+9y2-6xy-6x-12y+2021
2. H=2x2+4y2+4xy+4y+9
3. I= x2-4xy+5y2+10x-22y+28
4. K=x2+5y2-4xy+6x-14y+15
Cho X và Y là 2 số thực tuỳ ý , tìm giá trị nhỏ nhất của biểu thức sau :
A= x2+5y2+4xy+6x+16y+32
Lời giải:
$A=(x^2+4y^2+4xy)+y^2+6x+16y+32$
$=(x+2y)^2+6(x+2y)+(y^2+4y)+32$
$=(x+2y)^2+6(x+2y)+9+(y^2+4y+4)+19$
$=(x+2y+3)^2+(y+2)^2+19\geq 0+0+19=19$
Vậy $A_{\min}=19$. Giá trị này đạt tại $x+2y+3=y+2=0$
$\Leftrightarrow y=-2; x=1$
Đúng 1
Bình luận (2)
Chứng minh rằng:
x2 + 5y2 + 2x - 4xy - 10y + 14 > 0 với mọi x, y.
Chứng minh rằng:
x2 + 5y2 + 2x - 4xy - 10y + 14 > 0 với mọi x, y.
Câu hỏi của KiKyo - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo nhé!
Đúng 0
Bình luận (0)
Tìm x, y thuộc Z thỏa mãn: 2x - 5y + 4xy = 6
kho....................wa..................troi.......................thi.....................ret.................lanh................wa..................tich............................ung.........................ho..............minh......................cho....................do....................lanh
Đúng 0
Bình luận (0)
tìm cặp số nguyên x,y thỏa mãn ( x - 1)2 + 5y2 = 6
Answer:
\(2+5y^2=6\)
\(5y^2=6-2\)
\(5y^2=4\)
\(5y^2=2^2\)
\(\Rightarrow5y=2\)
\(y=2\div5\)
\(y=\dfrac{2}{5}\)
Vậy \(y=\dfrac{2}{5}\)
Đúng 0
Bình luận (0)
tìm cặp số nguyên x,y thỏa mãn ( x - 1)2 + 5y2 = 6
`(x - 1)^2 + 5y^2 = 6`
`<=>` $\left[\begin{matrix} (x - 1)^2 = 0\\ (x - 1)^2 = 2\end{matrix}\right.$
`<=>` $\left[\begin{matrix} y = -1; 1\\ y = -1; 1\end{matrix}\right.$\
`<=>` $\left[\begin{matrix} x = 0 ; y = -1; 1\\ x = 2 ; y = -1; 1\end{matrix}\right.$
Đúng 0
Bình luận (0)
(x-1)2≥0 => 5y2≤6 => y2≤6/5
Mà y2 là số chính phương => y2 = 0 hoặc y2 = 1
TH1: y2= 0
=> (x-1)2 = 6 (vô lý)
TH2: y2 = 1 => y = -1 hoặc 1
=> 5y2=5
=> (x-1)2=6-5=1
=> x-1 = 1 hoặc x-1 = -1
=> x=2 hoặc x=0
Vậy các cặp số tm là (0,1); (0,-1); (2,1); (2,-1)
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức:
C = x2 - 4xy + 5y2 +10x - 22y +28
\(C=\left(x^2+4y^2+25-4xy+10x-20y\right)+\left(y^2-2y+1\right)+2\)
\(C=\left(x-2y+5\right)^2+\left(y-1\right)^2+2\ge2\)
\(C_{min}=2\) khi \(\left\{{}\begin{matrix}x=-3\\y=1\end{matrix}\right.\)
Đúng 1
Bình luận (0)