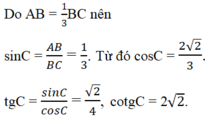Cho tam giác ABC vuông tại A, cosC = 1/3.Tính sinB, sinC
SG
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A
a) Biết cosC = 5/13. Tính sinC, cosB và tanC
b) Biết tanB = 1/5 . Tính E = sinB - 3cosB/2sinB + 3cosB
\(a,cosC=\dfrac{5}{13}\\ Ta,có:cos^2C+sin^2C=1\\ \Rightarrow sinC=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\\ cosB+sinC=1\\ \Leftrightarrow cosB+\dfrac{12}{13}=1\\ \Rightarrow cosB=\dfrac{1}{13}\\ tanC=\dfrac{sinC}{cosC}=\dfrac{\dfrac{12}{13}}{\dfrac{5}{13}}=\dfrac{12}{5}\)
Đúng 3
Bình luận (0)
\(b,tanB=\dfrac{1}{5}\Rightarrow\dfrac{sinB}{cosB}=\dfrac{1}{5}\Rightarrow cosB=5sinB\\ E=\dfrac{sinB-3cosB}{2sinB+3cosB}=\dfrac{sinB-3.5.sinB}{2sinB+3.5.sinB}=\dfrac{-14sinB}{17sinB}=-\dfrac{14}{17}\)
Đúng 1
Bình luận (0)
cho tam giác abc có 3 góc nhọn. Vẽ đường cáo AD, BE, CF cắt nhau tại H. Chứng minh:
a) \(0< cos^2A+cos^2B+cos^2C< 1\)
b)\(2< sin^2A+sin^2B+sin^2C< 3\)
c)sinA + sinB + sinC < 2( cosA + cosB + cosC)
d)sinB . cosC + sinC . cosB = sinA
e)tanA + tanB + tanC = tanA . tanB . tanC
: Tam giác ABC vuông tại A. Khẳng định nào sau đây đúng?
A. sinB = sinC B. cosB = cosC C. tanB = cotC D. cotB = cotC
Cho tam giác ABC vuông tại A Biết :
1. sinc=1/3 tính AC. 2. cosc=2/5 tính AC
mong mn giúp đỡ
Cho tam giác ABC vuông tại A, có AB = 1/3BC. Hãy tính sinC, cosC, tgC, cotgC.
Tìm tính chất của tam giác ABC thỏa:
sinA+sinB+sinC=1-cosA+cosB+cosC
TL:
sinA+sinB+sinC=1-cosA+cosB+cosC => Tam giác ABC Vuông tại A
Vế trái = sinA + sinB + sinC
= 2sin(A + B)/2.cos(A - B)/2 + 2sinC/2.cosC/2
= 2cosC/2.cos(A - B)/2 + 2sinC/2.cosC/2
= 2cosC/2[cos(A - B)/2 + sinC/2]
=2.cosC/2.[cos(A - B)/2 + cos(A + B)/2]
= 4.cosC/2.cosB/2.cosA/2
Vế phải = 1 - cosA + cosB + cosC
= 2sin²A/2 + 2cos(B + C)/2.cos(B - C)/2
= 2.sinA/2[sinA/2 + cos(B - C)/2] (vì cos(B + C)/2 = sinA/2)
= 2.sinA/2[cos(B + C)/2 + cos(B - C)/2
= 4.sinA/2.cosB/2.cosC/2
Vậy sinA + sinB + sinC = 1 - cosA + cosB + cosC
<=> cosA/2.cosB/2.cosC/2 = sinA/2.cosB/2.cosC/2
<=> cosB/2.cosC/2(sinA/2 - cosA/2) = 0
mà cosB/2 ≠ 0 và cosC/2 ≠ 0
=> sinA/2 = cosA/2
<=> A/2 = 45o
<=> A = 90o
tam giác ABC vuông tại A
cho tam giác abc có sinb+sinc=2sina và cosb +cosc = 2cosa . chung minh tam giac abc đều
Theo định lí sin:
\(sinB=\dfrac{b}{2R};sinC=\dfrac{c}{2R};sinA=\dfrac{a}{2R}\)
Theo định lí cosin:
\(cosB=\dfrac{a^2+c^2-b^2}{2ac};cosC=\dfrac{a^2+b^2-c^2}{2ab};cosA=\dfrac{b^2+c^2-a^2}{2bc}\)
Theo giả thiết ta có:
\(\left\{{}\begin{matrix}sinB+sinC=2sinA\\cosB+cosC=2cosA\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{b}{2R}+\dfrac{c}{2R}=2.\dfrac{a}{2R}\\\dfrac{a^2+c^2-b^2}{2ac}+\dfrac{a^2+b^2-c^2}{2ab}=2.\dfrac{b^2+c^2-a^2}{2bc}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b+c=2a\\\dfrac{a^2b+bc^2-b^3}{2abc}+\dfrac{a^2c+b^2c-c^3}{2abc}=\dfrac{b^2+c^2-a^2}{bc}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b+c=2a\\\dfrac{\left(b+c\right)\left(a^2+bc-b^2-c^2+bc\right)}{2a}=b^2+c^2-a^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b+c=2a\\\dfrac{2a\left(a^2-b^2-c^2+2bc\right)}{2a}=b^2+c^2-a^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b+c=2a\\a^2-b^2-c^2+2bc=b^2+c^2-a^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b+c=2a\\a^2-b^2-c^2+bc=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b+c=2a\\\left(\dfrac{b+c}{2}\right)^2-b^2-c^2+bc=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b+c=2a\\3b^2+3c^2-6bc=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b+c=2a\\3\left(b-c\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b+c=2a\\b=c\end{matrix}\right.\)
\(\Rightarrow a=b=c\)
\(\Rightarrow\Delta ABC\) đều
Đúng 1
Bình luận (0)
cho tam giác abc nhọn. chứng minh rằng:
sinA+sinB+sinC<2(cosA+cosB+cosC)
Cho tam giác ABC vuông tại A, đường cao AH. Tính sinB, sinC, biết:
a, AB = 13, BH = 5
b, BH = 3, CH = 4
a) Áp dụng đlí Py - ta - go cho tam giác HAB ( ^H =90^o )
Ta có : \(AB^2=AH^2+BH^2\)
\(13^2=AH^2+5^2\)
\(AH^2=13^2-5^2\)
\(\Rightarrow AH=\sqrt{13^2-5^2}\)
\(\sin B=\frac{AH}{AB}=\frac{\sqrt{13^2-5^2}}{13}\approx0,923\)
Áp dụng hệ thức lượng cho tam giác ABC( ^A = 90^o ) , đường cao AH , ta có :
\(AH^2=BH.HC\Rightarrow HC=\frac{AH^2}{BH}=\frac{12^2}{5}=28,8\)
=> BC = 5 + 28,8 = 33,8
\(\sin C=\frac{AB}{BC}=\frac{13}{33,8}\approx0,384\)
Vậy : \(\sin B\approx0,923\)
\(\sin C\approx0,384\)