Bài 3 với bài 4 ạ giúp mình với


giúp mình bài 3 bài 4 với ạ
lần sau bạn chụp thẳng ra nha,đùng chụp ngang
 mọi người giúp mình câu 20 với bài 3 bài 4 với ạ
mọi người giúp mình câu 20 với bài 3 bài 4 với ạ
III
1 It's colder today than yesterday
2 It takes 4 hours to travel by car and fives hours by train
3 We were busier at work today than everyday
4 Jane's sister cooks worse than her
5 Nobody in this team can play football as well as Tom
IV
1 D
2 A
Giúp mình bài 3 và bài 4 với ạ 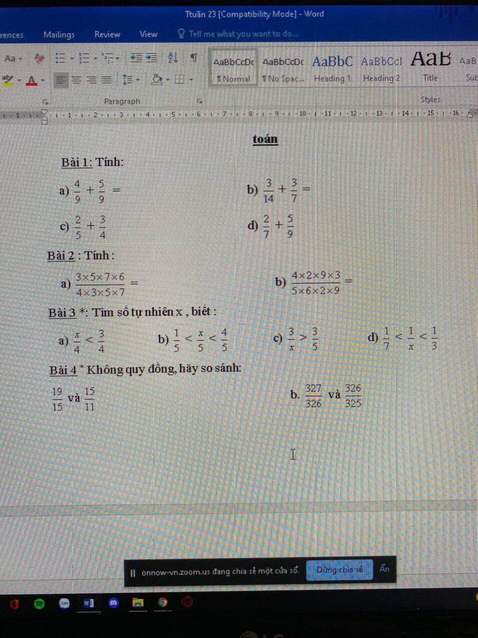
e thay dấu = cho tất cả phsố trog bài 3 rồi tìm x , khi tìm x thì coi dấu của bài r nói x lớn hoặc nhỏ hơn số đó là đc
Giải giúp mình với ạ! ( Bài 3 và bài 4 nha )
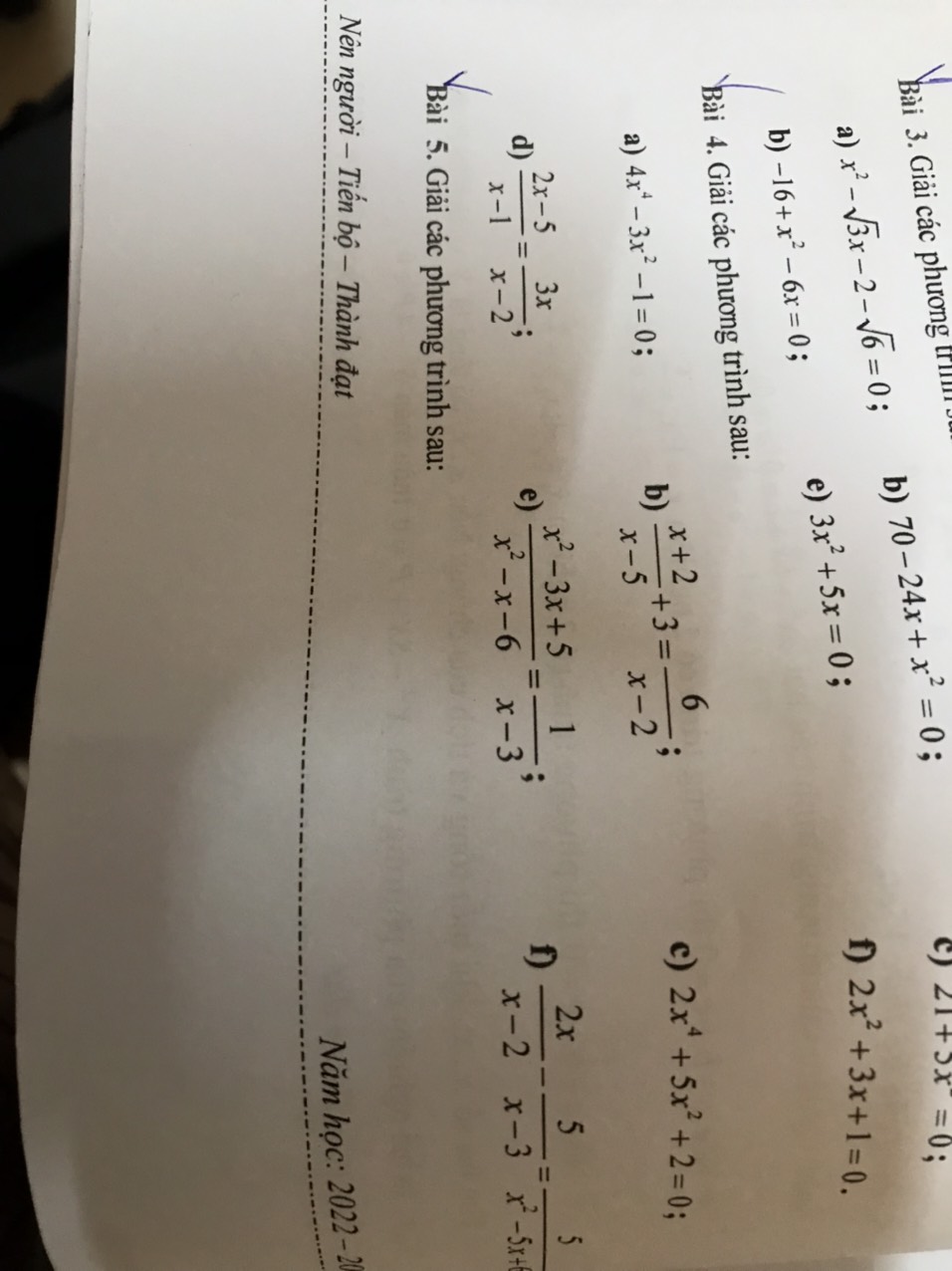

giúp mình bài 4 với bài 5 với ạ
4:
a: =>4x^4-4x^2+x^2-1=0
=>(x^2-1)(4x^2+1)=0
=>x^2-1=0
=>x=1 hoặc x=-1
b: ĐKXĐ: x<>5; x<>2
PT =>\(\dfrac{x-2}{x-5}+3=\dfrac{6}{x-2}\)
=>\(x^2-4x+4+3\left(x^2-7x+10\right)=6x-30\)
=>4x^2-25x+34-6x+30=0
=>4x^2-31x+64=0
=>\(x\in\varnothing\)
c: =>x^2(2x^2+5)+2=0
=>x^2(2x^2+5)=-2(vôlý)
d: =>(2x-5)(x-2)=3x(x-1)
=>3x^2-3x=2x^2-4x-5x+10
=>x^2+6x-10=0
=>\(x=-3\pm\sqrt{19}\)
e: ĐKXĐ: x<>3; x<>-2
PT =>x^2-3x+5=x+2
=>x^2-4x+3=0
=>(x-3)(x-1)=0
=>x=1(nhận) hoặc x=3(loại)
f: ĐKXĐ: x<>2; x<>3
PT =>2x(x-3)-5(x-2)=5
=>2x^2-6x-5x+10-5=0
=>2x^2-11x+5=0
=>2x^2-10x-x+5=0
=>(x-5)(2x-1)=0
=>x=1/2 hoặc x=5


Giải giúp mình bài Bài 4 Bài 5 với ạ
Mn làm giúp mình bài 3, 4 với ạ. Mai mình phải nộp rồi
Bài 3:
PTHH: \(2R+O_2\xrightarrow[]{t^O}2RO\)
Theo PTHH: \(n_R=n_{RO}\) \(\Rightarrow\dfrac{3,6}{M_R}=\dfrac{6}{M_R+16}\)
\(\Rightarrow M_R=24\) (Magie)
Bài 2:
PTHH: \(2Al+6HCl\rightarrow2AlCl_3+3H_2\uparrow\)
Ta có: \(n_{Al}=\dfrac{8,1}{27}=0,3\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}n_{HCl}=0,9\left(mol\right)\\n_{AlCl_3}=0,3\left(mol\right)\\n_{H_2}=0,45\left(mol\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}V_{H_2}=0,45\cdot22,4=10,08\left(l\right)\\m_{AlCl_3}=0,3\cdot133,5=40,05\left(g\right)\\m_{ddHCl}=\dfrac{0,9\cdot36,5}{7,3\%}=450\left(g\right)\\m_{H_2}=0,45\cdot2=0,9\left(g\right)\end{matrix}\right.\)
Mặt khác: \(m_{dd\left(saup/ứ\right)}=m_{Al}+m_{ddHCl}-m_{H_2}=457,2\left(g\right)\)
\(\Rightarrow C\%_{AlCl_3}=\dfrac{40,05}{457,2}\cdot100\%\approx8,76\%\)
Giúp mình bài 2 , bài 4 với ạ ;-;

Bài 2 :
$n_{Ba(OH)_2} = 0,3(mol) ; n_{BaSO_3} = 0,08(mol)$
TH1 : $Ba(OH)_2$ dư
$Ba(OH)_2 + SO_2 \to BaSO_3 + H_2O$
$n_{SO_2} = n_{BaSO_3} = 0,08(mol)$
$V_{SO_2} = 0,08.22,4 = 1,792(lít)$
TH2 : có tạo muối axit
SO2 + Ba(OH)2 → BaSO3 + H2O
0,08......0,08..............0,08..............(mol)
2SO2 + Ba(OH)2 → Ba(HSO3)2
0,44........0,22......................................(mol)
$V_{SO_2} = (0,08 + 0,44).22,4 = 11,648(lít)$
Bài 4 :
$n_{BaCO_3} = 0,05(mol)$
CO2 + Ba(OH)2 → BaCO3 + H2O
0,05......0,05..............0,05..............(mol)
2CO2 + Ba(OH)2 → Ba(HCO3)2
..............0,2..................0,2....................(mol)
Ba(HCO3)2 \(\xrightarrow{t^o}\)BaCO3 + CO2 + H2O
0,2.....................0,2........................(mol)
m = 0,2.197 = 39,4 gam
4. \(n_{BaCO_3}=\dfrac{9,85}{197}=0,05\left(mol\right)\)
Bảo toàn nguyên tố Ba => \(n_{Ba\left(HCO_3\right)_2}=0,25-0,05=0,2\left(mol\right)\)
Lọc kết tủa đem nung thì thu được m gam chất rắn : BaCO3
Bảo toàn nguyên tố Ba =>\(n_{BaCO_3}=n_{Ba\left(HCO_3\right)_2}=0,2\left(mol\right)\)
=> \(m=0,2.197=39,4\left(g\right)\)
 Giúp mình bài 2b với bài 3 với ạ
Giúp mình bài 2b với bài 3 với ạ
2b)
Áp dụng BĐT bunhiacopxki có:
\(\left(1+1\right)\left(x^4+y^4\right)\ge\left(x^2+y^2\right)^2\)
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x+y\right)^2\)\(\Leftrightarrow x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Rightarrow2\left(x^4+y^4\right)\ge\dfrac{\left(x+y\right)^4}{4}\Leftrightarrow x^4+y^4\ge\dfrac{1}{8}.\left(x+y\right)^4\)
Dấu "=" xảy ra khi x=y
3)
Áp dụng bđt Holder có:
\(\left(x^3+y^3+z^3\right)\left(1+1+1\right)\left(1+1+1\right)\ge\left(x+y+z\right)^3\)
\(\Leftrightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\)
Dấu "=" xảy ra khi x=y=z
3)(Nếu không dùng Holder)
Với x,y,z >0, ta có bđt sau:\(2x^3+2y^3+2z^3\ge xy\left(x+y\right)+yz\left(y+z\right)+xz\left(x+z\right)\) (1)
Thật vậy (1)\(\Leftrightarrow\left(x+y\right)\left(x^2-xy+y^2\right)-xy\left(x+y\right)+\left(y+z\right)\left(y^2-yz+z^2\right)-yz\left(y+z\right)+\left(z+x\right)\left(z^2-zx+x^2\right)-zx\left(x+z\right)\ge0\)
\(\Leftrightarrow\left(x+y\right)\left(x-y\right)^2+\left(y+z\right)\left(y-z\right)^2+\left(z+x\right)\left(z-x\right)^2\ge0\) (lđ)
Áp dụng AM-GM có:
\(x^3+y^3+z^3\ge3xyz\)
\(\Leftrightarrow\dfrac{2\left(x^3+y^3+z^3\right)}{3}\ge2xyz\) (2)
Từ (1) và (2), cộng vế với vế \(\Rightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge xy\left(x+y\right)+yz\left(x+z\right)+xz\left(x+z\right)+2xyz\)
\(\Leftrightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge\left(x+y\right)\left(y+z\right)\left(z+x\right)\)
\(\Leftrightarrow8\left(x^3+y^3+z^3\right)\ge3\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
\(\Leftrightarrow9\left(x^3+y^3+z^3\right)\ge x^3+y^3+z^3+3\left(x+y\right)\left(y+z\right)\left(z+x\right)=\left(x+y+z\right)^3\)
\(\Rightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\) (đpcm)