Tìm giá trị nhỏ nhất, lớn nhất của hàm số:
y = Cos2x + Sinx +1
1/ tìm TXĐ chủa hàm số y = căn 1 - cosx /2 + sinx.
2/ tìm tập giá trị của hàm số y = 2-cos2x.
3/ Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau :
a) y=1 + 2sinx b)y=1 - 2cos^2x
4/ Tìm giá trị nhỏ nhất của hàm số y=tan^2x - 2tanx +3.
1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
Cho hàm số y = cos 2 x + sin x + x cos x 1 + s i n 2 x . Tổng các giá trị lớn nhất và nhỏ nhất của hàm số bằng
A. 1 2
B. 1
C. -1
D. - 1 2
Tìm giá trị lớn nhất của hàm số y = cos 2 x + sin x + 3 trên R.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm giá trị lớn nhất của hàm số y = c o s 2 x + s i n x + 3 trên R.
A. m a x R y = 4
B. m a x R y = 5
C. m a x R y = 15 4
D. m a x R y = 17 4
Giá trị lớn nhất của hàm số y = c o s 2 x + s i n x + 1 bằng
A. 2
B. 11/4
C. 1
D. 9/4
Tìm giá trị nhỏ nhất của hàm số y = 2 . cos 2 x + 4 . sin x trên đoạn 0 , π 2
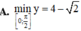
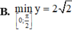
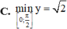
![]()
Gọi M m , theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sinx+cos2x+sin3xtrên đoạn 0 ; π . Tính P = M+m
A. ![]()
B. 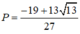
C. 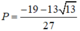
D. 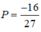
Gọi M , m theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = s inx+ cos 2 x + sin 3 x trên đoạn 0 ; π . Tính P = M + m
A. P = 16 27
B. P = − 19 + 13 13 27
C. P = − 19 − 13 13 27
D. P = − 16 27
tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
\(y=\dfrac{sinx+3cosx+1}{sinx-cosx+2}\)
\(ĐK:sinx-cosx\ne-2\)
\(< =>2y-1=sinx\left(1-y\right)+cosx\left(y+3\right)\)
Theo Bunhiacopxki:
\(\left[sinx\left(1-y\right)+cosx\left(y+3\right)\right]^2\)\(\le\left(sin^2x+cos^2x\right)\left[\left(1-y\right)^2+\left(y+3\right)^2\right]\)
\(< =>\left(2y-1\right)^2\le2y^2+4y+10\)
\(< =>2y^2-8y-9\le0\)
=> Bấm máy tìm Max, Min của y
(Sry máy tính của t bị ngáo không bấm ra)
\(\Rightarrow y.sinx-y.cosx+2y=sinx+3cosx+1\)
\(\Rightarrow\left(y-1\right)sinx-\left(y+3\right)cosx=1-2y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất
\(\Rightarrow\left(y-1\right)^2+\left(y+3\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow2y^2-8y-9\le0\)
\(\Rightarrow\dfrac{4-\sqrt{34}}{2}\le y\le\dfrac{4+\sqrt{34}}{2}\)
\(y_{max}=\dfrac{4+\sqrt{34}}{2}\) ; \(y_{min}=\dfrac{4-\sqrt{34}}{2}\)
\(y=\dfrac{sinx+3cosx+1}{sinx-cosx+2}\)
\(\Leftrightarrow y.sinx-y.cosx+2y=sinx+3cosx+1\)
\(\Leftrightarrow\left(y-1\right)sinx-\left(y+3\right).cosx=1-2y\)
Phương trình có nghiệm khi \(\left(y-1\right)^2+\left(y+3\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow y^2-2y+1+y^2+6y+9\ge4y^2-4y+1\)
\(\Leftrightarrow2y^2-8y-9\le0\)
\(\Leftrightarrow\dfrac{4-\sqrt{34}}{2}\le y\le\dfrac{4+\sqrt{34}}{2}\)
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sin x - cos 2 x . Hỏi mệnh đề nào trong các mệnh đề sau là sai?
A. 2 M m = 2
B. M + m = 2
C. M m = 0
D. M - m = 2
Ta có
y = sin x = cos 2 x = sin x - 1 - 2 sin 2 x = 2 sin 2 x + sin x - 1
Đặt t = sin(x), - 1 ≤ t ≤ 1
Ta sẽ đi tìm GTLN và GTNN của hàm số y = g t = 2 t 2 + t - 1 trên đoạn [ -1;1 ]
Ta có g t = - 2 t 3 - t + 1 , - 1 ≤ t ≤ 1 2 2 t 3 + t - 1 , 1 2 ≤ t ≤ 1
* Xét hàm số h t = - 2 t 3 - t + 1 trên đoạn - 1 ; 1 2
Dễ dàng tìm được
M a x r ∈ 1 2 ; 1 h t = 9 8 ⇔ t = - 1 4 M i n r ∈ 1 2 ; 1 h t = 0 ⇔ t = 1 2
* Xét hàm số k t = 2 t 3 + t - 1 trên đoạn 1 2 ; 1
Cũng dễ dàng tìm được
M a x r ∈ 1 2 ; 1 k t = 2 ⇔ t = 1 M i n r ∈ 1 2 ; 1 k t = 0 ⇔ t = 1 2
Qua hai trường hợp trên ta đi đến kết luận
M a x r ∈ - 1 ; 3 g t = 2 ⇔ t = 1 M i n r ∈ - 1 ; 3 g t = 0 ⇔ t = 1 2
Hay
M = M a x y = 2 ⇔ sin x = - 1 ⇔ x = - π 2 + k 2 π m = Miny = 0 ⇔ sin x = 1 2 ⇔ x = π 6 + k 2 π x = 5 π 6 + k 2 π
Đáp án C