Giải bpt
X2 +x-6>0
X2+7+12<=0
(X -2) (x +6) (2x +5)<=0
(1-x) (x2 -- 6)>0
Giải BPT
x2 - 2x + 8 < 0
X2 -2x +8 < 0
X2 -2x +1 +7 < 0
(x-1)2 +7 <0
mà (x-1)2 > 0 với mọi x
=> (x-1)2 +7>0 với mọi x
nên bpt vô nghiệm
x2= 1
x2=3
x2=5 với x<0
x2=7 với x<0
x2=9
(x-2)2=2
(x-4)2=4
(x-6)2=6
(x-8)2=8
(x-10)2=10
(x-\(\sqrt{3}\) )2=3
(x-\(\sqrt{5}\))2=5
\(x^2=1\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(x^2=3\Rightarrow\left[{}\begin{matrix}x=-\sqrt{3}\\x=\sqrt{3}\end{matrix}\right.\)
\(x^2=5\Rightarrow\left[{}\begin{matrix}x=-\sqrt{5}\\x=\sqrt{5}\end{matrix}\right.\Rightarrow x=-\sqrt{5}\left(vì.x< 0\right)\)
\(x^2=7\Rightarrow\left[{}\begin{matrix}x=-\sqrt{7}\\x=\sqrt{7}\end{matrix}\right.\Rightarrow x=-\sqrt{7}\left(vì.x< 0\right)\)
\(x^2=9\Rightarrow\left[{}\begin{matrix}x=-3\\x=3\end{matrix}\right.\)
\(\left(x-2\right)^2=2\Rightarrow\left[{}\begin{matrix}x-2=-\sqrt{2}\\x-2=\sqrt{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2-\sqrt{2}\\x=2+\sqrt{2}\end{matrix}\right.\)
\(\left(x-4\right)^2=4\Rightarrow\left[{}\begin{matrix}x-2=-2\\x-2=2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
\(\left(x-6\right)^2=6\Rightarrow\left[{}\begin{matrix}x-6=-\sqrt{6}\\x-6=\sqrt{6}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=6-\sqrt{6}\\x=6+\sqrt{6}\end{matrix}\right.\)
\(\left(x-8\right)^2=8\Rightarrow\left[{}\begin{matrix}x-8=-2\sqrt{2}\\x-8=2\sqrt{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=8-2\sqrt{2}\\x=2+2\sqrt{2}\end{matrix}\right.\)
\(\left(x-10\right)^2=10\Rightarrow\left[{}\begin{matrix}x-10=-\sqrt{10}\\x-10=\sqrt{10}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=10-\sqrt{10}\\x=10+\sqrt{10}\end{matrix}\right.\)
\(\left(x-\sqrt{3}\right)^2=3\Rightarrow\left[{}\begin{matrix}x-\sqrt{3}=-\sqrt{3}\\x-\sqrt{3}=\sqrt{3}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=2\sqrt{3}\end{matrix}\right.\)
\(\left(x-\sqrt{5}\right)^2=5\Rightarrow\left[{}\begin{matrix}x-\sqrt{5}=-\sqrt{5}\\x-\sqrt{5}=\sqrt{5}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=2\sqrt{5}\end{matrix}\right.\)
Tập nghiệm của hệ bất phương trình 2 x 2 + 9 x + 7 > 0 x 2 + x - 6 < 0 là:
A. S = [-1;2]
B. S = (-1;2)
C. S = (- ∞ ;-1)
D. S = R
Chọn B.
Ta có:
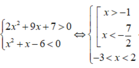
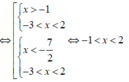
Vậy tập nghiệm hệ bất phương trình là S = (-1;2).
9x2+12x+4=0
x2+\(\dfrac{1}{4}\)=x
4-\(\dfrac{12}{x}\)+\(\dfrac{9}{x^2}\)=0
(a) \(9x^2+12x+4=0\)
\(\Leftrightarrow\left(3x+2\right)^2=0\Leftrightarrow3x+2=0\Leftrightarrow x=-\dfrac{3}{2}\)
(b) \(x^2+\dfrac{1}{4}=x\)
\(\Leftrightarrow x^2-x+\dfrac{1}{4}=0\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2=0\Leftrightarrow x-\dfrac{1}{2}=0\Leftrightarrow x=\dfrac{1}{2}\)
(c) \(4-\dfrac{12}{x}+\dfrac{9}{x^2}=0\left(x\ne0\right)\)
\(\Leftrightarrow\left(2-\dfrac{3}{x}\right)^2=0\Leftrightarrow2-\dfrac{3}{x}=0\Leftrightarrow x=\dfrac{3}{2}\)
giúp mình giải bài này với
giải phương trình
a) ( x2-2x+1)- 4 = 0(x2-2x+1)-4=0
b) x2-x= -2x+2x2-x=-2x+2
c) 4x2+4x+1= x24x2+4x+1= x2
d)x2-5x+6= 0x2-5x+6=0
\(a.\left(x^2-2x+1\right)-4=0\\\Leftrightarrow \left(x-1\right)^2-2^2=0\\\Leftrightarrow \left(x-1-2\right)\left(x-1+2\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x+1\right)=0\\\Leftrightarrow \left[{}\begin{matrix}x-3=0\\x+1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
Vậy tập nghiệm của phương trình trên là \(S=\left\{3;-1\right\}\)
\(b.x^2-x=-2x+2\\\Leftrightarrow x^2-x+2x-2=0\\\Leftrightarrow x\left(x-1\right)+2\left(x-1\right)=0\\\Leftrightarrow \left(x+2\right)\left(x-1\right)=0\\\Leftrightarrow \left[{}\begin{matrix}x+2=0\\x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
Vậy tập nghiệm của phương trình trên là \(S=\left\{-2;1\right\}\)
\(c.4x^2+4x+1=x^2\\ \Leftrightarrow4\left(x^2+x+\frac{1}{4}\right)-x^2=0\\ \Leftrightarrow4\left(x+\frac{1}{2}\right)^2-x^2=0\\ \Leftrightarrow\left[2\left(x+\frac{1}{2}\right)-x\right]\left[2\left(x-\frac{1}{2}\right)+x\right]=0\\ \Leftrightarrow\left[{}\begin{matrix}2\left(x+\frac{1}{2}\right)-x=0\\2\left(x+\frac{1}{2}\right)+x=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x+1-x=0\\2x+1+x=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\frac{1}{3}\end{matrix}\right.\)
Vậy tập nghiệm của phương trình trên là \(S=\left\{-1;-\frac{1}{3}\right\}\)
\(d.x^2-5x+6=0\\ \Leftrightarrow x^2-2x-3x+6=0\\\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x-2\right)=0\\\Leftrightarrow \left[{}\begin{matrix}x-2=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
Vậy tập nghiệm của phương trình trên là \(S=\left\{2;3\right\}\)
-x-6=-10
7-x=-5
6x+4x=-100
(x-2) (x+1)=0
x2=100
Giải chi tiết rõ ràng nha cảm ơn mọi người
-x-6=-10
-x=(-10)+6
-x=-4
x=4
7-x=-5
x=7-(-5)
x=2
-x-6=-10
-x =-10+6
-x =4
x =-4
7-x=-5
-x =-5-7
-x =-12
x =12
Giải hệ phương trình: x 3 + x y 2 − 10 y = 0 x 2 + 6 y 2 = 10
x 3 + x y 2 − 10 y = 0 x 2 + 6 y 2 = 10 < = > x 3 + x y 2 − ( x 2 + 6 y 2 ) y = 0 (1) x 2 + 6 y 2 = 10 (2)
Từ phương trình (1) ta có:
x 3 + x y 2 − ( x 2 + 6 y 2 ) y = 0 < = > x 3 + x y 2 − x 2 y − 6 y 3 = 0 < = > x 3 − 2 x 2 y + x 2 y − 2 x y 2 + 3 x y 2 − 6 y 3 = 0 < = > ( x − 2 y ) ( x 2 + x y + 3 y 2 ) = 0 < = > x = 2 y x 2 + x y + 3 y 2 = 0
+ Trường hợp 1: x 2 + x y + 3 y 2 = 0 < = > ( x + y 2 ) 2 + 11 y 2 4 = 0 = > x = y = 0
Với x= y = 0 không thỏa mãn phương trình (2).
+ Trường hợp 2: x= 2y thay vào phương trình (2) ta có:
4 y 2 + 8 y 2 = 12 < = > y 2 = 1 < = > y = 1 = > x = 2 y = − 1 = > x = − 2
Vậy hệ phương trình có 2 nghiệm ( x ; y ) ∈ { ( 2 ; 1 ) ; ( − 2 ; − 1 ) }
1) 9.(x+7)-12=24
2) 12-3x=(-30)
3) 95-105:x=60
4) x+35=12
5) (-24)-(10-x)=43
6) 6-(17+x)=(-16)
7) (x-18)-(-3)=0
8) 25-(x-6)=(-1)
Ai giải hết mình tick
1) 9 . (x + 7) - 12 = 24
9 . (x + 7) = 24 + 12
9 . (x + 7) = 36
x + 7 = 36 : 9
x + 7 = 4
x = 4 - 7
x = -3
2) 12 - 3x = -30
3x = 12 - (-30)
3x = 12 + 30
3x = 42
x = 42 : 3
x = 14
3) 95 - 105 : x = 60
105 : x = 95 - 60
105 : x = 35
x = 105 : 35
x = 3
4) x + 35 = 12
x = 12 - 35
x = -23
5) (-24) - (10 - x) = 43
-24 - 10 + x = 43
-34 + x = 43
x = 43 - (-34)
x = 43 + 34
x = 77
6) 6 - (17 + x) = -16
6 - 17 - x = -16
-11 - x = -16
x = -11 - (-16)
x = -11 + 16
x = 5
7) (x - 18) - (-3) = 0
x - 18 + 3 = 0
x - 18 = 0 - 3
x - 18 = -3
x = -3 + 18
x = 15
8) 25 - (x - 6) = -1
25 - x + 6 = -1
25 - x = -1 - 6
25 - x = -7
x = 25 - (-7)
x = 25 + 7
x = 32
1)9.(x+7)-12=24
9.(x+7)=24+12
9.(x+7)=36
x+7=36:9
x+7=4
x=4-7
x=-3
2)12-3x=-30
3x=12-(-30)
3x=42
x=42:3
x=14
12/7 x 2/11 + 12/11 x 15/7 - 12/7 x 6/11
GIẢI HỘ VS MK CẦN GẤP ĐÚNG THÌ MK TK 2 CÁI CX ĐC , TRÌNH BÀY RÕ RA NHÉ CÓ 1 PẦN THUI
\(\frac{12}{7}\times\frac{2}{11}+\frac{12}{11}\times\frac{15}{7}-\frac{12}{7}\times\frac{6}{11}\)
\(=\frac{12}{7}\times\frac{2}{11}+\frac{12}{7}\times\frac{15}{11}-\frac{12}{7}\times\frac{6}{11}\)
\(=\frac{12}{7}\times\left(\frac{2}{11}+\frac{15}{11}-\frac{6}{11}\right)\)
\(=\frac{12}{7}\times1=\frac{12}{7}\)
\(\frac{12}{7}.\frac{2}{11}+\frac{12}{11}.\frac{15}{7}-\frac{12}{7}.\frac{6}{11}\)
= \(\frac{24}{77}\)+\(\frac{180}{77}\)-\(\frac{72}{77}\)
=\(\frac{132}{77}\)
\(\frac{12}{7}\cdot\frac{2}{11}+\frac{12}{11}\cdot\frac{15}{7}-\frac{12}{7}\cdot\frac{6}{11}\)
\(=\frac{12}{7}\cdot\frac{2}{11}+\frac{12}{7}\cdot\frac{15}{11}-\frac{12}{7}\cdot\frac{6}{11}\)
\(=\frac{12}{7}\cdot\left(\frac{2}{11}+\frac{15}{11}-\frac{6}{11}\right)\)
\(=\frac{12}{7}\cdot1\)
\(=\frac{12}{7}\)
1) (-49) - x - 13= (-6)
2) 74+ x - (-12)= 5
3) 21-( 29 + x ) = (-12)
4) 14-(x-17)=(-31)
5) (-5) (3-x)= (-15)+30
6) (-2)5 - (-x)= (-19)
7) (-18)-(x-17)=12
8) (-15) - ( x - 7 ) = 23
9) x là bội của 6 và (-8)<x<13
Ai giải nhanh, hết luôn mình tick nha nhớ ghi cách giải
1)x=-30
2)x=-81
3)x=4
4)x=62
5)x=6
6)-13
7)-13
8)-31
9)x=-6;0;6;12
tk minh nha