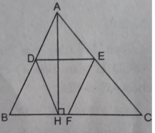
Cho ∆ABC nhọn (AB < AC). Gọi D; E và F lần lượt là trung điểm AB; AC và BC.
a) Chứng minh DEFB là hình bình hành.
b) Chứng minh ADFE là hình bình hành.
c) Chứng minh DECF là hình bình hành.
d) Gọi I là trung điểm DE. Chứng minh A; I và F thẳng hàng.
H24
Những câu hỏi liên quan
Cho tam giác ABC nhọn có H là trực tâm Gọi D E lần lượt là giao điểm của BH với AC ,CH với AB Chứng minh rằng tam giác AEC và ADB là hai tam giác đồng dạng Cho tam giác ABC nhọn có H là trực tâm Gọi D E lần lượt là giao điểm của BH với AC ,CH với AB Chứng minh rằng tam giác AEC và ADB là hai tam giác đồng dạng
a) Xét ΔAEC vuông tại E và ΔADB vuông tại D có
\(\widehat{BAD}\) chung
Do đó: ΔAEC\(\sim\)ΔADB(g-g)
Đúng 1
Bình luận (1)
Cho tam giác nhọn ABC (ABAC). Gọi D là trung điểm AB E là trung điểm AC M là trung điểm BCa) Cho DE 10cm tính BC?b) tứ giác BDEC là gì? tại sao?c) Chứng minh tứ giác BDEM là hình bình hành
Đọc tiếp
Cho tam giác nhọn ABC (AB<AC). Gọi D là trung điểm AB
E là trung điểm AC
M là trung điểm BC
a) Cho DE= 10cm tính BC=?
b) tứ giác BDEC là gì? tại sao?
c) Chứng minh tứ giác BDEM là hình bình hành
a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: \(DE=\dfrac{BC}{2}\)
hay BC=20(cm)
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC (ABAC). Gọi D là trung điểm AB E là trung điểm AC M là trung điểm BCa) Cho DE 10cm tính BC?b) tứ giác BDEC là gì? tại sao?c) Chứng minh tứ giác BDEM là hình bình hành
Đọc tiếp
Cho tam giác nhọn ABC (AB<AC). Gọi D là trung điểm AB
E là trung điểm AC
M là trung điểm BC
a) Cho DE= 10cm tính BC=?
b) tứ giác BDEC là gì? tại sao?
c) Chứng minh tứ giác BDEM là hình bình hành
a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\)
hay BC=20(cm)
b: Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC (ABAC). Gọi D là trung điểm AB E là trung điểm AC M là trung điểm BCa) Cho DE 10cm tính BC?b) tứ giác BDEC là gì? tại sao?c) Chứng minh tứ giác BDEM là hình bình hành
Đọc tiếp
Cho tam giác nhọn ABC (AB<AC). Gọi D là trung điểm AB
E là trung điểm AC
M là trung điểm BC
a) Cho DE= 10cm tính BC=?
b) tứ giác BDEC là gì? tại sao?
c) Chứng minh tứ giác BDEM là hình bình hành
a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔBAC
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\)
hay BC=20(cm)
b: Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC (AC > AB), đường cao AH. Gọi D, E, F theo thứ tự là trung điểm của AB, AC, BC. Tính độ dài HE.
A C 2 = A H 2 + H C 2 = 8 2 + 6 2 = 10 2 ⇒ AC = 10cm;
HE = 1/2 AC = 1/2.10 = 5 (cm).
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có AB < AC. Gọi D, E, F lần lượt là trung điểm của AB, AC, BC.
Chứng minh tứ giác BDEF là hình bình hành?
Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BF và DE=BF
hay BDEF là hình bình hành
Đúng 1
Bình luận (0)
Cho tam giác nhọn ABC (ABAC). Gọi D là trung điểm AB E là trung điểm AC M là trung điểm BCa) tứ giác BDEC là hình gì? tại sao?b) chứng minh tứ giác BDEM là hình bình hành
Đọc tiếp
Cho tam giác nhọn ABC (AB<AC). Gọi D là trung điểm AB
E là trung điểm AC
M là trung điểm BC
a) tứ giác BDEC là hình gì? tại sao?
b) chứng minh tứ giác BDEM là hình bình hành
a, Vì D,E là trung điểm AB,AC nên DE là đtb tg ABC
Do đó \(DE=\dfrac{1}{2}BC;DE//BC\)
Vậy BDEC là hình thang
b, Vì \(DE=\dfrac{1}{2}BC\) nên \(DE=BM\left(=\dfrac{1}{2}BC\right)\)(do M là trung điểm BC)
Mà DE//BC nên DE//BM
Do đó BDEM là hình bình hành
Đúng 1
Bình luận (0)
Cho △ nhọn ABC (AB < AC), hai đường cao BD và CE (E thuộc AB, D thuộc AC). Gọi giao điểm của BD và CE là H. Chứng minh: BH.BD + CH.CE = BC²
Gọi \(AH\cap BC=F\)
Xét \(\Delta BHF\) và \(\Delta BCD\) có: \(\left\{{}\begin{matrix}\widehat{BFH}=\widehat{BDC}=90^0\\\widehat{HBF}=\widehat{CBD}\end{matrix}\right.\)
\(\Rightarrow\Delta BHF\sim\Delta BCD\) (g.g) \(\Rightarrow\dfrac{BF}{BH}=\dfrac{BD}{BC}\Rightarrow BF.BC=BH.BD\)
Chứng minh tương tự ta có: \(CH.CE=CF.BC\)
\(\Rightarrow BH.BD+CH.CE=BF.BC+CF.BC=\left(BF+CF\right)BC=BC^2\)
Đúng 1
Bình luận (0)
Cho ∆ABC nhọn (AB < AC). Gọi D là trung điểm của AB. Dựng DE song song với AC cắt BC tại E. Gọi F đối xứng C qua D. Gọi G đối xứng F qua A. Gọi H là giao điểm của AC và BG.a) Chứng minh EB = EC.b) Chứng minh AFBC là hình bình hành.c) Chứng minh AB song song với CG.d) Chứng minh BC = 2HD.
a: Xét ΔABC có
D là trung điểm của AB
DE//AC
Do đó: E là trung điểm của BC
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, AB < AC, đường cao AD. Gọi E, F lần lượt là hình chiếu vuông góc của D trên AB, AC.
c) Chứng minh: \(tan^3C=\dfrac{BE}{CF}\)




