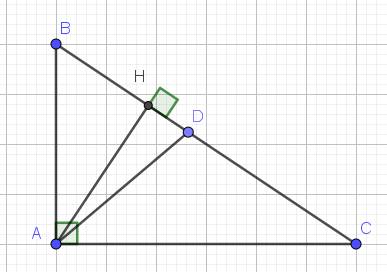
Cho tam giác ABC vuông tại A có AB = 9cm, AC = 12cm, đường cao AH. Tính BC, BK, KC và AK.
MB
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AB=9cm,AC=12cm,đường cao AH.Tính BC,AH,BH,CH.
Áp dụng định lý Pitago: \(BC=\sqrt{AB^2+AC^2}=15\left(cm\right)\)
Hệ thức lượng:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=7,2\left(cm\right)\)
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=5,4\left(cm\right)\)
\(CH=BC-BH=9,6\left(cm\right)\)
Đúng 2
Bình luận (0)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=9^2+12^2=225\)
hay BC=15(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot15=9\cdot12=108\)
hay AH=7,2(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{AB^2}{BC}=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=15-5,4=9,6(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AH là đường cao. BC=25cm, AH= 12cm. Tính AC, AB, HB, HC
Cho tam giác ABC vuông tại A có đường cao AH, BH = 1,8cm; AC = 4cm. Tính HC, BC, AB, AH ?
ta co \(AH^2=BH\cdot HC\Rightarrow AH^2=1,8HC\)
ap dung dl pitago vao tam giac vuong AHC co \(AH^2+CH^2=AC^2\Rightarrow1,8HC+HC^2=16\)
\(\Rightarrow CH^2+1,8CH-16=0\Rightarrow\left(CH-3,2\right)\left(CH+5\right)=0\)
\(\Rightarrow CH=3,2\) (do BH>0)
\(\Rightarrow AH^2=1,8\cdot CH=5.76\Rightarrow AH=2,4\)
\(BH+HC=BC\Rightarrow BC=1,8+3,2=5\)
ap dung dl pitago ta tinh dc \(AB^2+AC^2=BC^2\Rightarrow AB=3\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AH là đường cao. Biết AH=12cm,AM=13cm ( AM là đường trung tuyến). Tính BC, AB,HB,AC,HC
Cho tam giác ABC vuông tại A và AB =12cm, AC =16cm .Đường phân giác góc A cắt BC tại D
a) Tính BC ,BD vad CD ĐS: BC =20cm , BD≈8,6cm ,DC≈11,4 cm
b) Vẽ đường cao AH .Tính AH ,HD và AD ĐS: AH ≈9.6 cm , HD ≈1,4cm , AD ≈9,7 cm
Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
Áp dụng tính chất đường phân giác:
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
Mà: $BD+DC=BC=20$ nên:
$BD=20:(3+4).3=\frac{60}{7}$ (cm)
$CD= 20:(3+4).4=\frac{80}{7}$ (cm)
b.
$AH=2S_{ABC}:BC=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$HD = BD-BH = \frac{60}{7}-7,2=\frac{48}{35}$ (cm)
$AD = \sqrt{AH^2+HD^2}=\sqrt{9,6^2+(\frac{48}{35})^2}=\frac{48\sqrt{2}}{7}$ (cm)
Đúng 2
Bình luận (0)
a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=12^2+16^2=20^2\)
=>\(BC=20\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{12}=\dfrac{CD}{16}\)
=>\(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=BC=20
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{20}{7}\)
=>\(BD=\dfrac{20}{7}\cdot3=\dfrac{60}{7}\left(cm\right);CD=\dfrac{20}{7}\cdot4=\dfrac{80}{7}\left(cm\right)\)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot20=12\cdot16=192\)
=>\(AH=\dfrac{192}{20}=9,6\left(cm\right)\)
Ta có: ΔAHB vuông tại H
=>\(HB^2+AH^2=AB^2\)
=>\(HB^2=12^2-9,6^2=51,84\)
=>\(HB=\sqrt{51,84}=7,2\left(cm\right)\)
=>HC=BC-HB=12,8(cm)
Vì CD<CH
nên D nằm giữa C và H
=>CD+DH=CH
=>\(DH=12.8-\dfrac{80}{7}=\dfrac{48}{35}\left(cm\right)\)
ΔAHD vuông tại H
=>\(AH^2+HD^2=AD^2\)
=>\(AD^2=\left(\dfrac{48}{35}\right)^2+9,6^2=\dfrac{4608}{49}\)
=>\(AD=\sqrt{\dfrac{4608}{49}}=\dfrac{48\sqrt{2}}{7}\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A (AB AC) có AH là đường cao. Gọi M,N lần lượt là trung điểm của BC,AB.a) CM: tam giác ABH đồng dạng tam giác CBA và AB^2BH.BCb) Tia phân giác góc ABC cắt AC tại D. Vẽ đường thẳng AK vuông góc BD tại K.CM: tam giác BHD đồng dạng tam giác BKC.c) CM: MN vuông góc AB và BH.BMBN.BAd) Từ B vẽ đường thẳng vuông góc với BC cắt MN tại I, CI cắt AH tại O.CM: ON song song BC (câu chủ yếu)
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao. Gọi M,N lần lượt là trung điểm của BC,AB.
a) CM: tam giác ABH đồng dạng tam giác CBA và \(AB^2=BH.BC\)
b) Tia phân giác góc ABC cắt AC tại D. Vẽ đường thẳng AK vuông góc BD tại K.
CM: tam giác BHD đồng dạng tam giác BKC.
c) CM: MN vuông góc AB và \(BH.BM=BN.BA\)
d) Từ B vẽ đường thẳng vuông góc với BC cắt MN tại I, CI cắt AH tại O.
CM: ON song song BC (câu chủ yếu)
Cho tam giác ABC vuông tại A, đường cao AH. Có AH = 2,4 cm; BC = 5 cm. Tính HB, HC, AB, AC ?
Cho tam giác ABC vuông tại A, AH là đường cao. Biết AB=15cm,HC=16cm.Tính BC,AH,HB,AC.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có AB=AC=10cm, BC=12cm, Vẽ cung tròn tâm A có bán kính 9cm. Cung đó có cắt đường thẳng BC hay không, có cắt cạnh BC hay không? Vì sao?
cho ΔABC vuông tại A , đường cao AH. Biết AB = 9cm, AC= 12cm, tia phân giác của góc BAH cắt BC tại D, tia phân giác của góc ACB cắt AH, AD theo thứ tự tại F,K
a, tính độ dài BC
b, ΔADC cân
c, DF//AB
d, DF cắt AB tại M chứng minh rằng HM//AD
e, AH.BC=AB.AC
VẼ hình hộ mik luôn ạ❗ mik xin cảm ơn