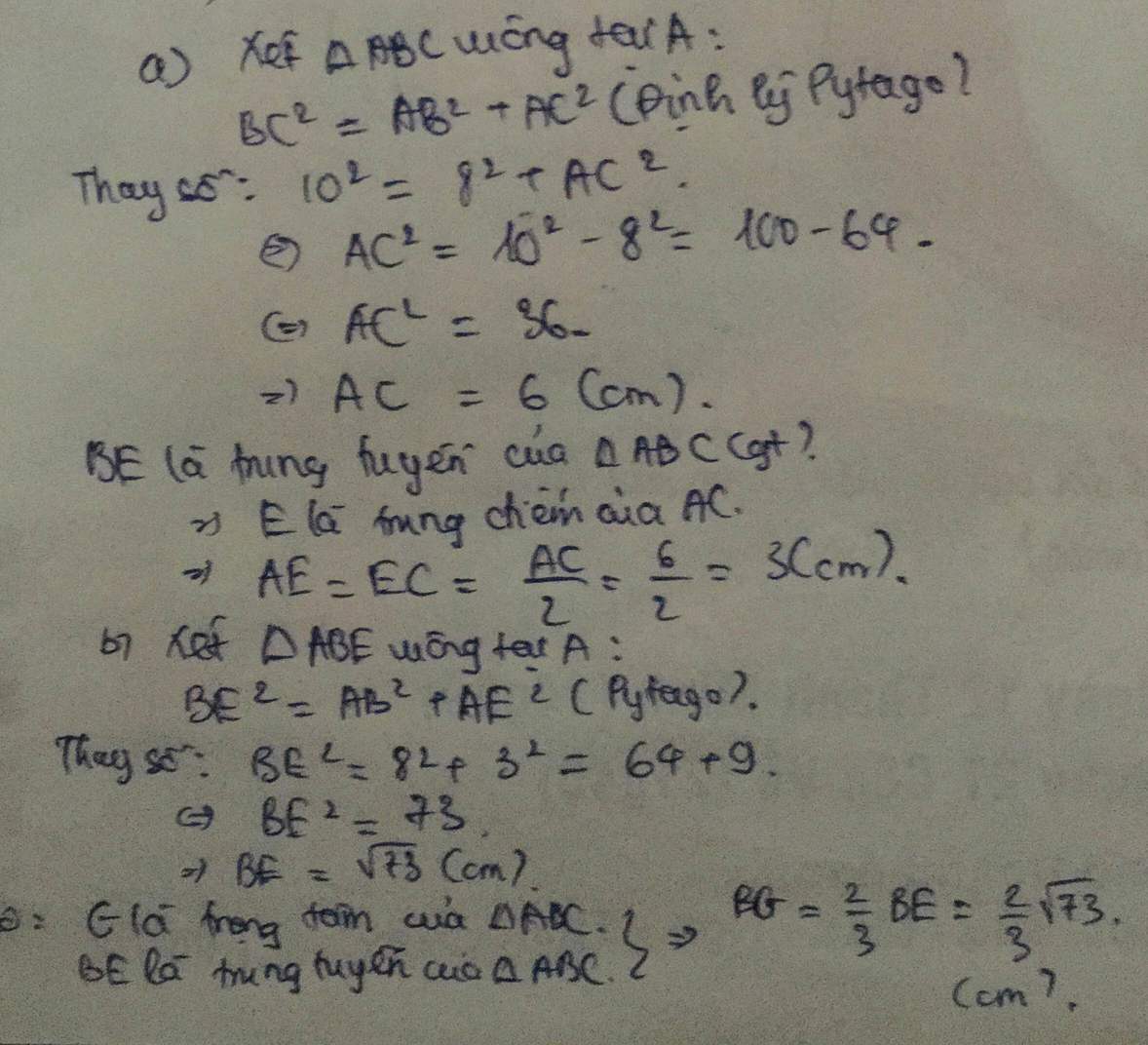cho tam giác ABC cân tại A,AB=10cm,AC=12cm,các trung tuyến AD,BE đi qua G.TÍNH BE
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
ND
Những câu hỏi liên quan
cho tam giác ABC cân tại A,AB=10cm,AC=12cm,các trung tuyến AD,BE đi qua G.qua b kẻ đường song song với gc cắt ad tại k.chứng minh bc là trung trực của gk
Cho tam giác abc vuông tại A có ab =8cm, bc=10cm.Trung tuyến ad cắt trung tuyến be ở g.Tính be.bg?
AC=căn 10^2-8^2=6cm
AE=AC/2=3cm
BE=căn AB^2+BE^2=căn 8^2+3^2=căn 73(cm)
Xét ΔABC có
AD,BE là trung tuyến
AD cắt BE tại G
=>G là trọng tâm
=>BG=2/3BE=2/3*căn 73(cm)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, có AB =8cm, BC =10cm. Trung tuyến AD cắt trung tuyến BE ở G
a, Tính AC, AE
b, Tính BE, BG
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=10^2-8^2=36\)
hay AC=6(cm)
Ta có: E là trung điểm của AC
nên \(AE=\dfrac{AC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
b: Áp dụng định lí Pytago vào ΔABE vuông tại A, ta được:
\(BE^2=BA^2+AE^2\)
\(\Leftrightarrow BE^2=3^2+8^2=73\)
hay \(BE=\sqrt{73}\left(cm\right)\)
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC
BE là đường trung tuyến ứng với cạnh AC
AD cắt BE tại G
Do đó: G là trọng tâm của ΔABC
Suy ra: \(BG=\dfrac{2}{3}BE=\dfrac{2\sqrt{73}}{3}\left(cm\right)\)
Đúng 1
Bình luận (0)
Bài 9:Cho tam giác ABC vuông tại A có AB = 8cm;BC= 10cm. Trung tuyến AD cắt trung tuyến BE ở G.
a) Tính AC và AE.
b) Tính BE và BG
Cho tam giác ABC cân tại A, đường cao AD, O là trung điểm của AC, điểm E đối xứng với điểm D qua điểm O.
a) Chứng minh tứ giác AECD là hình chữ nhật.
b) Gọi I là trung điểm của AD, chứng tỏ I là trung điểm của BE. c)
Cho AB = 10cm, BC = 12cm, tính diện tích tam giác OAD.
d) Đường thẳng OI cắt AB tại K. Tìm điều kiện của tam giác ABC để tứ giác AEDL là hình thang cân.
* Giả thiết kết luận bạn tự trình bày nhé
a) Ta có : AO = OC (gt) ( do D đối xứng với E qua O ) \(\widehat{ADC}=90^o\)(gt) . Vậy ADCE là hình chữ nhật
b) ADCE là hình chữ nhật thì AE // DC , AE = DC . Mà DC = BD ( do tam giác ABC cân ) . Suy ra , AE = BD
=> ABDE là hình bình hành . I là trung điểm của AD thì I là trung điểm của BE
c) Áp dụng định lí Py - ta - go cho tam giác vuông ABD
\(AD=\sqrt{AB^2-\left(\frac{BC}{2}\right)^2}=\sqrt{10^2-6^2}=8\left(cm\right)\)
\(S_{\Delta OAD}=\frac{1}{2}S_{ADC}=\frac{1}{2}.\frac{1}{2}.AD.DC=\frac{1}{4}.8.6=12\left(cm\right)\)
d) Tứ giác ABDE là hình bình hành do đó AKDE là hình thang
Để AKDE là hình thang cân thì KD = AE
Mà \(\hept{\begin{cases}KD=\frac{1}{2}AC\\AE=\frac{1}{2}BC\end{cases}\Rightarrow}AC=BC\)
\(\Rightarrow\Delta ABC\)là tam giác đều
Cho tam giác ABC vuông ở A có: Ab=8cm, BC=10cm. Trung tuyến AD cắt trung tuyến BE ở G
a, Tính Ac và AE
b, Tính Be và BG
c, Kéo Dài CG cắt AB tại K. Tính Ck
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=10^2-8^2=36\)
hay AC=6(cm)
Ta có: E là trung điểm của AC(gt)
nên \(AE=\dfrac{AC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
b) Áp dụng định lí Pytago vào ΔABE vuông tại A, ta được:
\(BE^2=AB^2+AE^2\)
\(\Leftrightarrow BE^2=8^2+3^2=73\)
hay \(BE=\sqrt{73}\left(cm\right)\)
Xét ΔABC có
BE là đường trung tuyến ứng với cạnh AC(gt)
AD là đường trung tuyến ứng với cạnh BC(gt)
BE cắt AD tại G
Do đó: G là trọng tâm của ΔABC(Tính chất ba đường trung tuyến của tam giác)
Suy ra: \(BG=\dfrac{2}{3}BE=\dfrac{2}{3}\cdot\sqrt{73}=\dfrac{2\sqrt{73}}{3}\left(cm\right)\)
Đúng 2
Bình luận (0)
cho tam giác ABC có AD là phân giác góc BAC , D thuộc BC
a) cho biết AB = 10cm , AC = 12cm , BD = 4cm . tính độ dài BC
b) qua D kẻ đường thẳng song song với AB , cắt AC tại E. Gọi M là trung điểm của AB , AD , cắt EM tại I , BE cắt MD tại K. Chứng minh rằng : IE/IM = KD/KM. từ đó chứng minh IK song song ED.
cho tam giác ABC có AD là phân giác góc BAC , D thuộc BC.
a) cho biết AB = 10cm , AC = 12cm , BD = 4cm . tính độ dài BC
b) qua D kẻ đường thẳng song song với AB , cắt AC tại E. Gọi M là trung điểm của AB , AD , cắt EM tại I , BE cắt MD tại K. Chứng minh rằng : IE/IM = KD/KM. từ đó chứng minh IK song song ED.
a) Xét \(\Delta ABC:\)
AD là phân giác \(\widehat{BAC}\left(gt\right).\)
\(\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{AC}\) (Tính chất phân giác).
\(\Rightarrow\dfrac{BD}{CD+BD}=\dfrac{AB}{AC+AB}.\\ \Rightarrow\dfrac{BD}{BC}=\dfrac{AB}{AC+AB}.\)
Thay: \(\dfrac{4}{BC}=\dfrac{10}{12+10}.\Rightarrow BC=8,8\left(cm\right).\)
Vậy \(BC=8,8\left(cm\right).\)
Đúng 0
Bình luận (0)
cho tam giác abc có ab=ac = 10cm,bc = 12cm,các đường cao ad và ce cắt nhau tại h. a) tính ad b) tam giác abd đồng dạng với tam giác cbe c) tính be,hd
b: Xét ΔABD vuông tại D và ΔCBE vuông tại E có
\(\widehat{B}\) chung
Do đó: ΔABD\(\sim\)ΔCBE
Đúng 1
Bình luận (1)