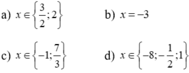Giải phương trình sau: \(|1+4x|-|7x-2|=0\)
TA
Những câu hỏi liên quan
giải phương trình sau
4x+1-\(\sqrt{3x^2+7x}-2\sqrt{3x-1}\)= 0
ĐKXĐ: \(x\ge\dfrac{1}{3}\)
PT \(\Leftrightarrow2\left(x-\sqrt{3x-1}\right)+\left[\left(2x+1\right)-\sqrt{3x^2+7x}\right]=0\)
\(\Leftrightarrow\dfrac{2\left(x^2-3x+1\right)}{x+\sqrt{3x-1}}+\dfrac{\left(2x+1\right)^2-\left(3x^2+7x\right)}{2x+1+\sqrt{3x^2+7x}}=0\)
\(\Leftrightarrow\left(x^2-3x+1\right)\left[\dfrac{2}{x+\sqrt{3x-1}}+\dfrac{1}{2x+1+\sqrt{3x^2+7x}}\right]=0\)
Cái ngoặc to vô nghiệm, đến đây bạn có thể giải.
Đúng 0
Bình luận (0)
Giải phương trình sau:
4x^4 - 7x^2 - 5x - 1 = 0
\(4x^4-7x^2-5x-1=0\)
<=> \((4x^4+4x^3+x^2)-\left(4x^3+4x^2+x\right)-\left(4x^2+4x+1\right)=0\)
<=> \(x^2\left(4x^2+4x+1\right)-x\left(4x^2+4x+1\right)-\left(4x^2+4x+1\right)=0\)
<=> \(\left(4x^2+4x+1\right)\left(x^2-x-1\right)=0\)
<=> \(\left(x+1\right)^2\left(x^2-x-1\right)=0\) => \(\orbr{\begin{cases}x+1=0\\x^2-x-1=0\end{cases}}\)
(+) \(x+1=0=>x=-1\)
(+) \(x^2-x-1=0\)
=> \(x_1=\frac{1+\sqrt{5}}{2};x_2=\frac{1-\sqrt{5}}{2}\)
Đúng 0
Bình luận (0)
Giải các phương trình sau:
a, 4x2 - 7x - 2 = 0
b, 4x2 + 5x - 6 = 0
a) ko vt lại đề
4x2-8x+x-2=0
=>4x(x-2)+(x-2)=0
=>(x-2)(4x+1)=0
......
b) bn tự làm nha
a)\(4x^2-7x-2=0\)
Ta có \(\Delta=7^2+4.4.2=81,\sqrt{\Delta}=9\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{7+9}{8}=2\\x=\frac{7-9}{8}=\frac{-1}{4}\end{cases}}\)
b)\(4x^2+5x-6=0\)
Ta có \(\Delta=5^2+4.4.6=121,\sqrt{\Delta}=11\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{-5+11}{8}=\frac{3}{4}\\x=\frac{-5-11}{8}=-2\end{cases}}\)
a) \(4x^2-7x-2=0\)\(\Leftrightarrow\left(4x^2-8x\right)+\left(x-2\right)=0\)
\(\Leftrightarrow4x\left(x-2\right)+\left(x-2\right)=0\)\(\Leftrightarrow\left(4x+1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}4x+1=0\\x-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{4}\\x=2\end{cases}}\)
Vậy tập nghiệm của pt là \(S=\left\{\frac{-1}{4};2\right\}\)
b) \(4x^2+5x-6=0\)\(\Leftrightarrow\left(4x^2+8x\right)-\left(3x+6\right)=0\)
\(\Leftrightarrow4x\left(x+2\right)-3\left(x+2\right)=0\)\(\Leftrightarrow\left(4x-3\right)\left(x+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}4x-3=0\\x+2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{4}\\x=-2\end{cases}}\)
Vậy tập nghiệm của pt là \(S=\left\{\frac{3}{4};-2\right\}\)
giải phương trình sau đặt biến phụ
1) 2x^3+7x^2+7x+2=0
2) x^3-8x^2-8x+1=0
3) x^5+2x^4+4x^2-3x+1=0
4) x^4+x^3+x^2+x+1=0
\(2x^3+7x^2+7x+2=0\)
\(\Leftrightarrow\left(2x^3+4x^2\right)+\left(3x^2+6x\right)+\left(x+2\right)=0\)
\(\Leftrightarrow2x^2\left(x+2\right)+3x\left(x+2\right)+\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x^2+3x+1\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left[2x\left(x+1\right)+\left(x+1\right)\right]=0\)
\(\Leftrightarrow\left(x+2\right)\left(x+1\right)\left(2x+1\right)=0\)
.......................................................................................
\(x^3-8x^2-8x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)-8x\left(x+1\right)=0\)
......................................................................................
Đúng 0
Bình luận (0)
Bài 3.giải các phương trình sau bằng cách đưa về phương trình tích.
a) (3x+1)(7x+3)=(5x-7)(3x+1)
b) x^2+10x+25-4x(x+5)=0
c) (4x-5)^2(16x^2-25)=0
d) (4x+3)^2=4(x^2-2x+1)
e) x^2-11x=28=0
f) 3x^3-3x^2-6x=0
Giải các phương trình sau:a)
x
−
1
3
x
−
5
;b)
x
+
1
2
+
1
x
+
3...
Đọc tiếp
Giải các phương trình sau:
a) x − 1 = 3 x − 5 ;
b) x + 1 2 + 1 x + 3 = 0 ;
c) 3 x 2 − 4 x − 7 = 0 ;
d) 7 x − 1 2 x + 1 + 2 x + 1 x 2 − 1 = 0 .
[Lớp 8]Bài 1. Giải phương trình sau đây:a) 7x+121;b) left(4x-10right)left(24+5xright)0;c) left|x-2right|2x-3;d) dfrac{x+2}{x-2}-dfrac{1}{x}dfrac{2}{xleft(x-2right)}. Bài 2. Giải bất phương trình sau đây và biểu diễn tập nghiệm trên trục số: dfrac{x-1}{3}-dfrac{3x+5}{2}ge1-dfrac{4x+5}{6}. Bài 3. Tìm giá trị lớn nhất của A-x^2+2x+9. Bài 4. Giải bài toán bằng cách lập phương trình:Một người đi xe máy dự định đi từ A đến B với vận tốc 36km/h. Nhưng khi thực hiện ngư...
Đọc tiếp

[Lớp 8]
Bài 1. Giải phương trình sau đây:
a) \(7x+1=21;\)
b) \(\left(4x-10\right)\left(24+5x\right)=0;\)
c) \(\left|x-2\right|=2x-3;\)
d) \(\dfrac{x+2}{x-2}-\dfrac{1}{x}=\dfrac{2}{x\left(x-2\right)}.\)
Bài 2. Giải bất phương trình sau đây và biểu diễn tập nghiệm trên trục số:
\(\dfrac{x-1}{3}-\dfrac{3x+5}{2}\ge1-\dfrac{4x+5}{6}.\)
Bài 3. Tìm giá trị lớn nhất của \(A=-x^2+2x+9.\)
Bài 4. Giải bài toán bằng cách lập phương trình:
Một người đi xe máy dự định đi từ A đến B với vận tốc 36km/h. Nhưng khi thực hiện người đó giảm vận tốc 6km/h nên đã đến B chậm hơn dự định là 24 phút.
Tính quãng đường AB.
Bài 5. Cho tam giác ABC vuông tại A có AH là đường cao. Vẽ HD⊥ AB (D ∈ AB), HE ⊥ AC (E∈ AC). AB=12cm, AC=16cm.
a) Chứng minh: ΔHAC đồng dạng với ΔABC;
b) Chứng minh AH2=AD.AB;
c) Chứng minh AD.AB=AE.AC;
d) Tính \(\dfrac{S_{ADE}}{S_{ABC}}.\)
Bài 4 :
24 phút = \(\dfrac{24}{60} = \dfrac{2}{5}\) giờ
Gọi thời gian dự định đi từ A đến B là x(giờ) ; x > 0
Suy ra quãng đường AB là 36x(km)
Khi vận tốc sau khi giảm là 36 -6 = 30(km/h)
Vì giảm vận tốc nên thời gian đi hết AB là x + \(\dfrac{2}{5}\)(giờ)
Ta có phương trình:
\(36x = 30(x + \dfrac{2}{5})\\ \Leftrightarrow x = 2\)
Vậy quãng đường AB dài 36.2 = 72(km)
Đúng 6
Bình luận (0)
Bài 3 :
\(A = -x^2 + 2x + 9 = -(x^2 -2x - 9) \\= -(x^2 - 2x + 1 + 10) = -(x^2 -2x + 1)+ 10\\=-(x-1)^2 + 10\)
Vì : \((x-1)^2 \geq 0\) ∀x \(\Leftrightarrow -(x-1)^2 \)≤ 0 ∀x \(\Leftrightarrow -(x-1)^2 + 10\) ≤ 10
Dấu "=" xảy ra khi và chỉ khi x - 1 = 0 ⇔ x = 1
Vậy giá trị nhỏ nhất của A là 10 khi x = 1
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
Bài 1 : giải những các phương trình sau A. X² - 2x - 3 = 0 B. X² - 3x = 0 C. X² - 4x - 5 = 0 D. 5x² + 2x - 7 = 0 E. 2x² - 8 = 0 G. 3x² -7x + 1 = 0 H. X² - 4x + 1 = 0
a: =>(x-3)(x+1)=0
=>x=3 hoặc x=-1
b: =>x(x-3)=0
=>x=0 hoặc x=3
c: =>(x-5)(x+1)=0
=>x=5 hoặc x=-1
d: =>5x^2+7x-5x-7=0
=>(5x+7)(x-1)=0
=>x=1 hoặc x=-7/5
e: =>x^2-4=0
=>x=2 hoặc x=-4
h: =>x^2-4x+4-3=0
=>(x-2)^2=3
=>\(x=2\pm\sqrt{3}\)
Đúng 1
Bình luận (2)
Giải phương trình sau:
a) x^3-x/49=0
b) x^2-7x+12=0
c)4x^2-3x-1=0
d) x^3-2x-4=0
\(a)x^3-\frac{x}{49}=0\)
\(\Leftrightarrow x\left(x^2-\frac{1}{7^2}\right)=0\)
\(\Leftrightarrow x=0\)Hoặc \(x^2-\frac{1}{7^2}=0\)
TH1: \(x\left(x^2-\frac{1}{7^2}\right)=0\\ x=\frac{0}{x^2-\frac{1}{7^2}}\\ \Leftrightarrow x=0\)
TH2: \(x\left(x^2-\frac{1}{7^2}\right)=0\\ x^2-\frac{1}{7^2}=\frac{0}{x}\\ x^2=0+\frac{1}{7^2}\\ x^2=\frac{1}{7^2}\\ x^2=\left(\frac{1}{7}\right)^2\\ \Leftrightarrow x=\frac{1}{7}\)
Vậy \(x=0\)Hoặc \(x=\frac{1}{7}\)
a) x3 - x/49 = 0
<=> x(x2 - 1/49) = 0
<=> x = 0 hoặc x2 - 1/49 = 0
<=> x = 0 hoặc x = +1/7
b) x2 - 7x + 12 = 0
<=> (x - 3)(x - 4) = 0
<=> x - 3 = 0 hoặc x - 4 = 0
<=> x = 3 hoặc x = 4
c) 4x2 - 3x - 1 = 0
<=> 4x2 + x - 4x - 1 = 0
<=> x(4x + 1) - (4x + 1) = 0
<=> (4x + 1)(x - 1) = 0
<=> 4x + 1 = 0 hoặc x - 1 = 0
<=> x = -1/4 hoặc x = 1
d) x3 - 2x - 4 = 0
<=> (x2 + 2x + 2)(x - 2) = 0
vì x2 + 2x + 2 khác 0 nên:
<=> x - 2 = 0
<=> x = 2