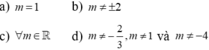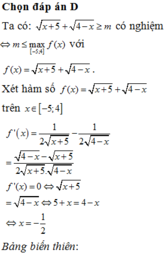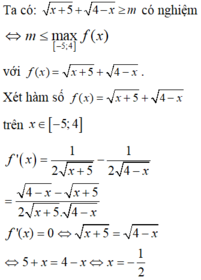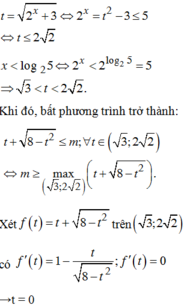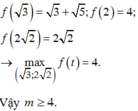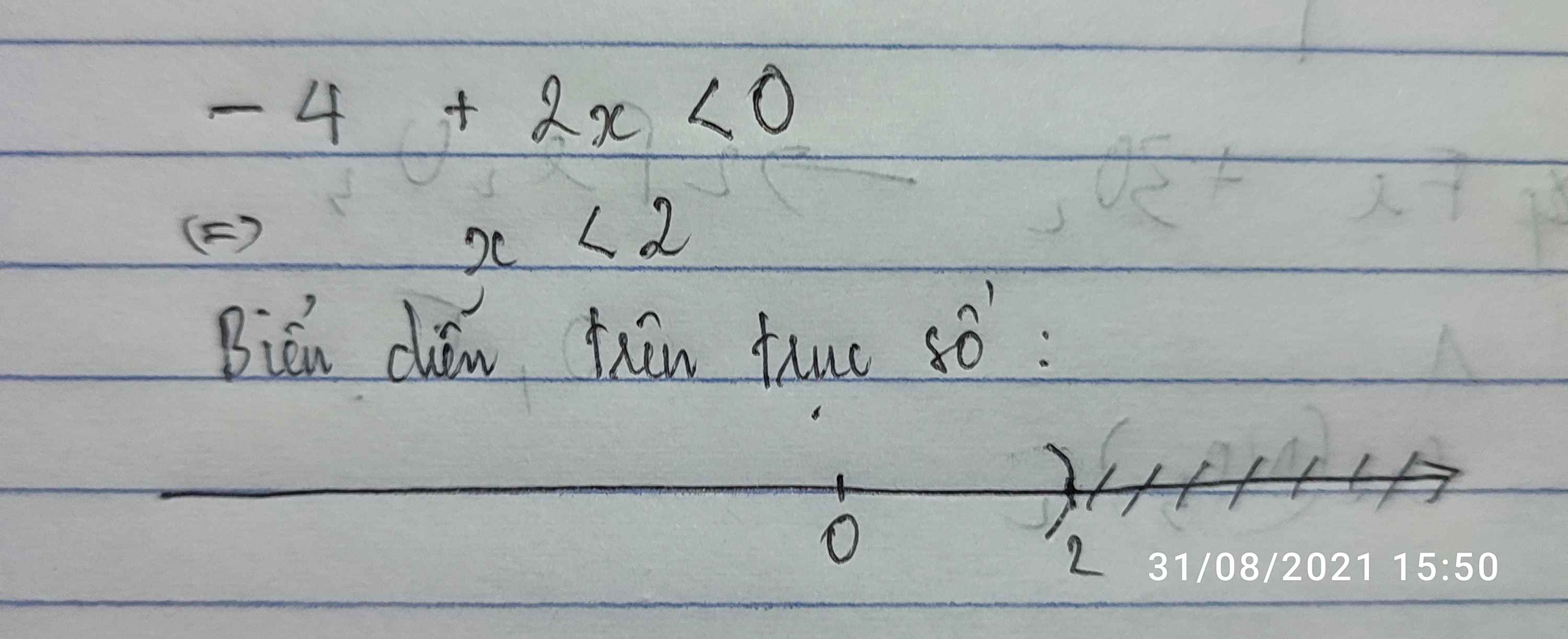Tìm m để của bất phương trình sau là số dương: 2x+m>5
H24
Những câu hỏi liên quan
HV
23 tháng 8 2021 lúc 21:05
Tìm m để nghiệm của bất phương trình sau đây đều là số âm:
2x+5<x+8−m
a,\(m\le3\)
b,\(m\ge2\)
c,\(m\ge-3\)
d,\(m\ge3\)
Lời giải:
$2x+5< x+8-m$
$\Leftrightarrow 2x-x< 8-5-m$
$\Leftrightarrow x< 3-m$
Để BPT có nghiệm đều là số âm thì $3-m\leq 0$
$\Lefrightarrow m\geq 3$
Đáp án D.
Đúng 0
Bình luận (0)
H24
18 tháng 3 2022 lúc 21:21
Bài 4:
a) Tìm m để phương trình sau có nghiệm duy nhất: 2x - mx + 2m - 1 = 0.
b) Tìm m để phương trình sau có vô số nghiệm: mx + 4 = 2x + m2.
c) Tìm m để phương trình sau có nghiệm duy nhất dương: (m2 - 4)x + m - 2 = 0
à bài này a nhớ (hay mất điểm ở bài này) ;v
Đúng 2
Bình luận (2)
xinloi cậu tớ muốn giúp lắm mà tớ ngu toán:)
Đúng 0
Bình luận (7)
a)Ta có \(2x-mx+2m-1=0\\ =>x\left(2-m\right)+2m-1=0\)
Để pt có nghiệm duy nhất thì \(a\ne0=>2-m\ne0\\=>m\ne2\)
b)Ta có \(mx+4=2x+m^2\\ =>mx+4-2x+m^2=0\\ =>\left(m-2\right)x=m^2-4\)
Để pt vô số nghiệm thì \(\left\{{}\begin{matrix}m-2=0\\m^2-4=0\end{matrix}\right.=>\left\{{}\begin{matrix}m=2\\m=\pm2\end{matrix}\right.\)\(=>m=2\)
c)Để pt có nghiệm duy nhất thì \(m^2-4\ne0>m\ne\pm2\)
Chắc vậy :v
Đúng 2
Bình luận (0)
Tìm m để các bất phương trình sau là bất phương trình bậc nhất:a)
m
−
1
x
2
−
2
m
−
1
x
0
;
b)
m
2
−
4
7
x...
Đọc tiếp
Tìm m để các bất phương trình sau là bất phương trình bậc nhất:
a) m − 1 x 2 − 2 m − 1 x > 0 ;
b) m 2 − 4 7 x − 5 ≤ 0 ;
c) 2 + 3 m 2 x − m 2 + 9 ≥ 0 ;
d) 3 m + 2 x − 5 m 2 + 3 m − 4
H24
26 tháng 2 2021 lúc 19:03
Câu 1: Giải và biện luận bất phương trình \(m^2x+m\ge2-4x\)
Câu 2: Tìm giá trị thực của tham số m để bất phương trình \(m\left(2x-1\right)\ge2x-1\) có tập nghiệm là \([1;+\infty)\)
1.
\(\Leftrightarrow\left(m^2+4\right)x\ge2-m\)
Do \(m^2+4>0\) ; \(\forall m\)
\(\Rightarrow x\ge\dfrac{2-m}{m^2+4}\)
2.
\(\Leftrightarrow2mx-2x\ge m-1\Leftrightarrow2\left(m-1\right)x\ge m-1\)
- Với \(m>1\Rightarrow m-1>0\)
\(\Rightarrow x\ge\dfrac{m-1}{2\left(m-1\right)}\Leftrightarrow x\ge\dfrac{1}{2}\) \(\Rightarrow D=[\dfrac{1}{2};+\infty)\)
- Với \(m< 1\Rightarrow m-1< 0\Rightarrow x\le\dfrac{m-1}{2\left(m-1\right)}\Leftrightarrow x\le\dfrac{1}{2}\) \(\Rightarrow D=(-\infty;\dfrac{1}{2}]\)
- Với \(m=1\Leftrightarrow0\ge0\Rightarrow D=R\)
Quan sát 3 TH ta thấy không tồn tại m để tập nghiệm của BPT là \([1;+\infty)\)
Đúng 2
Bình luận (0)
tìm điều kiện của m để phương trình sau là phương trình bậc nhất một ẩn: 4mx - 5x + 1 - m = 0
tìm điều kiện của m để bất phương trình sau là bất phương trình bậc nhất 1 ẩn: (5 - 4m) * x + 3 < 0
giúp mình nhanh lên nhé. Mình cảm ơn!!! ^-^
Tìm tất cả các giá trị nguyên dương của tham số m sao cho bất phương trình sau có nghiệm:
x
+
5
+
4
-
x
≥
m
A. 1 B. 2 C. 3 D. 4
Đọc tiếp
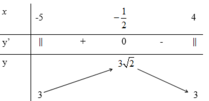
Tìm tất cả các giá trị nguyên dương của tham số m sao cho bất phương trình sau có nghiệm: x + 5 + 4 - x ≥ m
A. 1
B. 2
C. 3
D. 4
Tìm tất cả các giá trị nguyên dương của tham số m sao cho bất phương trình sau có nghiệm:
x
+
5
+
4
-
x
≥
m
A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Tìm tất cả các giá trị nguyên dương của tham số m sao cho bất phương trình sau có nghiệm: x + 5 + 4 - x ≥ m
A. 1
B. 2
C. 3
D. 4
Tìm tất cả các giá trị thực của tham số m để bất phương trình
2
x
+
3
+
5
-
2
x
≤
m
nghiệm đúng với mọi
x
∈
-
∞
;
log
2
5
A. m ≥ 4 B. m...
Đọc tiếp
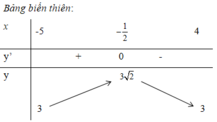
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 x + 3 + 5 - 2 x ≤ m nghiệm đúng với mọi x ∈ - ∞ ; log 2 5
A. m ≥ 4
B. m < 4
C. m ≥ 2 2
D. m < 2 2
a/ Giải bất phương trình sau: – 4 + 2x < 0. Hãy biểu diễn tập nghiệm trên trục số
b/ Cho A = \(\dfrac{x-5}{x-8}\) .Tìm giá trị của x để A dương.
b, ĐK: \(x\ne8\)
\(A=\dfrac{x-5}{x-8}>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-5>0\\x-8>0\end{matrix}\right.\\\left\{{}\begin{matrix}x-5< 0\\x-8< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>5\\x>8\end{matrix}\right.\\\left\{{}\begin{matrix}x< 5\\x< 8\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x>8\\x< 5\end{matrix}\right.\)
Đúng 1
Bình luận (0)
a/ -4 + 2x < 0
2x < 4
x < 2
b) Để A dương
\(\left[{}\begin{matrix}x< 5\\x>8\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời