Giải hệ pt
2X2 -XY+3Y2=13
x2 +4XY-2Y=-6
Giải pt nghiệm nguyên:
a,3y2-xy-2x+y+1=0
b,x2+3y2+4xy-2x-6y-24=0
c,x2+8y2+6xy+4x+8y-17=0
d,2x2+5y2-8x+3y=0
Các bn cứ giải giúp mik vói,mai mik phải nộp rồi
X2 + 4xy - 2Y2 =3 và 2X2 - xy + 3Y2 =4
giải hệ phương trình
x3y.( 2x4y3- 4xy -6)
1/2x^3y(2x^4y^3-4xy-6)
=1/2x^3y*2x^4y^3-1/2x^3y*4xy-1/2x^3y*6
=x^7y^4-2x^4y^2-3x^3y
x3y.( 2x4y3- 4xy -6)
1/2x^3y(2x^4y^3-4xy-6)
=1/2x^3y*2x^4y^3-1/2x^3y*4xy-1/2x^3y*6
=x^7y^4-2x^4y^2-3x^3y
(1) 1>.-3x.(x2 +7x- 1/3)
2. -5x2y4(3x2y3-2x3y2-xy)
3. \(\dfrac{1}{2}\)x3y .(2x4y3-4xy-6)
4. -2x.(3x+20
5. 3x.(5-2x)
6. 2x.(2x2-4x+5)
7. 4x3y2.(-2x2y+4x4-3y2)
8.\(\dfrac{1}{2}\)x3y.( 2x4y3- 4xy -6)
1: \(=-3x^3-21x^2+x\)
2: \(=-15x^4y^7+10x^5y^6+5x^3y^5\)
3: \(=x^7y^4-2x^4y^2-3x^3y\)
5: \(=15x-6x^2\)
6: \(=4x^3-8x^2+10x\)
7: \(=-8x^5y^3+16x^7y^2-12x^3y^4\)
8: \(=x^7y^4-2x^4y^2-3x^3y\)
Cho hai số thực x, y dương thỏa mãn: log 2 x 2 + 2 x y + 2 x + 1 3 - 3 y 2 - x y + x = 6 - x 2 - 4 x y - 6 y 2 Giá trị lớn nhất của biểu thức P=2x+5y bằng
![]()
![]()
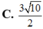
![]()
phân tích đa thức thành nhân tử
a) xy+y2-x-y
b) 25-x2+4xy-4y2
c) xy+yz-2y-2z
d) x2-6xy+9y2-25z2
e) 3x2-3y2-12x+12y
f) 4x3+4xy2+8x2y-16x
g) x2-5x+4
h) x4+5x2+4
i) 2x2+3x-5
k) x3-2x2+6x-5
l) x2-4x+3
Mong mọi người giúp đỡ em cảm ơn ạ
Bài làm
a) xy + y2 - x - y
= ( xy + y2 ) - ( x + y )
= y( x + y ) - ( x + y )
= ( x + y )( y - 1 )
b) 25 - x2 + 4xy - 4y2
= 25 - ( x2 - 4xy + 4y2 )
= 25 - ( x - 2y )2
= ( 5 - x + 2y )( 5 + x - 2y )
c) xy + xz - 2y - 2z
= ( xy + xz ) - ( 2y + 2z )
= x( y + z ) - 2( y + z )
= ( y + z )( x - 2 )
d) x2 - 6xy + 9y2 - 25z2
= ( x2 - 6xy + 9y2 ) - 25z2
= ( x - 3y )2 - 25z2
= ( x - 3y - 5z )( z - 3y + 5z )
e) 3x2 - 3y2 - 12x + 12y
= 3( x - y )( x + y ) - 12( x - y )
= ( x - y )[ 3( x + y ) - 12 ]
f) 4x3 + 4xy2 + 8x2y - 16x
= 4x( x2 + y2 + 2xy - 4 )
= 4x[ ( x + y)2 - 4 ]
= 4x( x + y - 2 )( x + y + 2 )
g) x2 - 5x + 4
= x2 - x - 4x + 4
= x( x - 1 ) - 4( x - 1 )
= ( x - 1 )( x - 4 )
h) x4 + 5x2 + 4
= x4 + x2 + 4x2 + 4
= x2( x2 + 1 ) + 4( x2 + 1 )
= ( x2 + 1 )( x2 + 4 )
i) 2x2 + 3x - 5
= 2x2 - 5x + 2x - 5
= 2x( x + 1 ) - 5( x + 1 )
= ( x + 1 )( 2x - 5 )
k) x3 - 2x2 + 6x - 5 ( không biết làm )
l) x2 - 4x + 3
= ( x2 - 4x + 4 ) - 1
= ( x - 2 )2 - 1
= ( x - 3 )( x - 1 )
# Học tốt #
1. cho x+y = 1 . tìm GTNN của biểu thức C = x2 + y2
2. cho x + 2y =1 . tìm GTNN của biểu thức P = x2 + 2y2
3. cho x + y =1 . tìm GTNN của biểu thức G = 2x2 + y2
4. cho x + y =1 . tìm GTNN của biểu thức H = x2 + 3y2
5. cho 2x + y =1 . tìm GTNN của biểu thức I = 4x2 + 2y2
6. tìm các số thực thõa mãn Pt :
2x2 + 5y2 + 8x - 10y + 13 = 0
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
a, -x2 + 2x + 3
b, x2 - 2x + 4y2 - 4y + 8 c, -x2 - y2 + xy + 2x + 2y + 4 d, x2 + 5y2 - 4xy - 2y + 2015 e, 2x2 + y2 + 6x + 2y + 2xy + 2018A= -x2+2x+3
=>A= -(x2-2x+3)
=>A= -(x2-2.x.1+1+3-1)
=>A=-[(x-1)2+2]
=>A= -(x+1)2-2
Vì -(x+1)2 ≤0=> A≤-2
Dấu "=" xảy ra khi
-(x+1)2=0 => x=-1
Vây A lớn nhất= -2 khi x= -1
B=x2-2x+4y2-4y+8
=> B= (x2-2x+1)+(4y2-4y+1)+6
=> B=(x-1)2+(2y+1)2+6
=> B lớn nhất=6 khi x=1 và y=-1/2